If internal resistance of a cell is proportional to current drawn from the cell. Then the best representation of terminal potential difference of a cell with current drawn from cell will be
A) 
B) 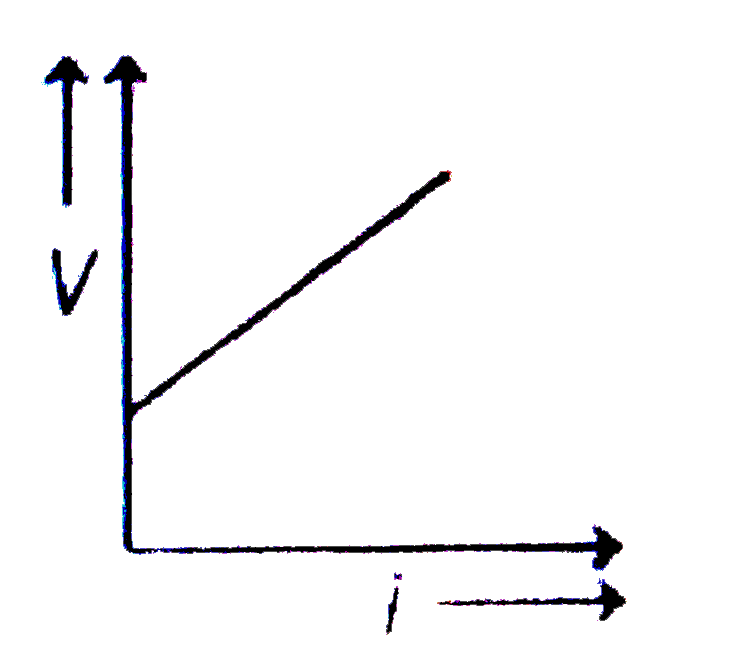
C) 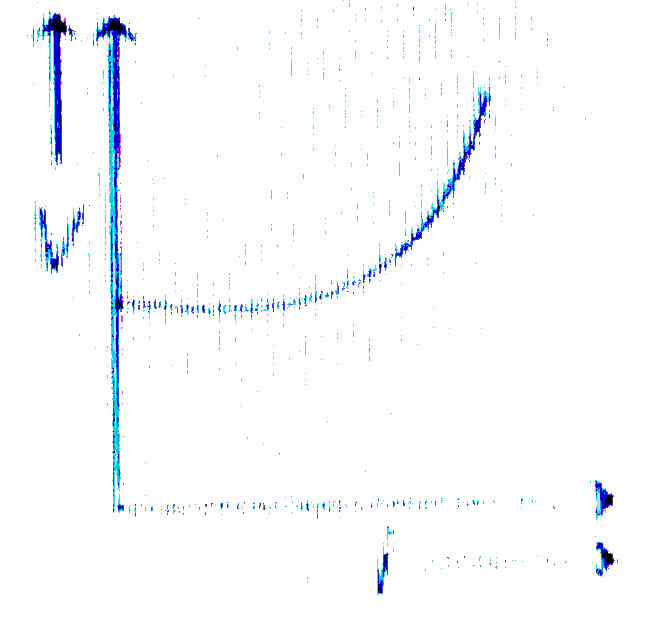
D) 
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the terminal potential difference (V) of a cell and the current (I) drawn from the cell, given that the internal resistance (R) of the cell is proportional to the current drawn.
1. Understanding the Relationship:
- We know that the terminal potential difference (V) of a cell can be expressed using Ohm's law:
V=E−I⋅R
where E is the electromotive force (emf) of the cell and R is the internal resistance.
2. Proportionality of Internal Resistance:
- According to the problem, the internal resistance R is proportional to the current I. We can express this as:
R=k⋅I
where k is a constant of proportionality.
3. Substituting Internal Resistance:
- Substituting R into the equation for terminal potential difference:
V=E−I⋅(k⋅I)
This simplifies to:
V=E−k⋅I2
4. Analyzing the Equation:
- The equation V=E−k⋅I2 indicates that the terminal potential difference V decreases as the square of the current I increases. This suggests a downward-opening parabola when plotted on a graph.
5. Graphical Representation:
- The graph of V versus I will show that as I increases, V decreases, and specifically, it will decrease in a quadratic manner due to the I2 term.
6. Identifying the Correct Option:
- Among the given options, we look for a graph that shows a downward curve, indicating that as the current increases, the terminal potential difference decreases. The correct representation would be a curve that starts at E (when I=0) and decreases as I increases, resembling a parabola opening downwards.
Conclusion:
The best representation of the terminal potential difference of a cell with the current drawn from the cell is a downward-opening parabola.
- We know that the terminal potential difference (V) of a cell can be expressed using Ohm's law:
V=E−I⋅R
where E is the electromotive force (emf) of the cell and R is the internal resistance.
- According to the problem, the internal resistance R is proportional to the current I. We can express this as:
R=k⋅I
where k is a constant of proportionality.
- Substituting R into the equation for terminal potential difference:
V=E−I⋅(k⋅I)
This simplifies to:
V=E−k⋅I2
- The equation V=E−k⋅I2 indicates that the terminal potential difference V decreases as the square of the current I increases. This suggests a downward-opening parabola when plotted on a graph.
- The graph of V versus I will show that as I increases, V decreases, and specifically, it will decrease in a quadratic manner due to the I2 term.
- Among the given options, we look for a graph that shows a downward curve, indicating that as the current increases, the terminal potential difference decreases. The correct representation would be a curve that starts at E (when I=0) and decreases as I increases, resembling a parabola opening downwards.
The best representation of the terminal potential difference of a cell with the current drawn from the cell is a downward-opening parabola.
Topper's Solved these Questions
Similar Questions
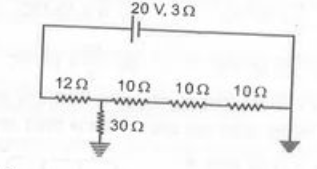
The electric current drawn from cell is
View SolutionDistinguish between emf and terminal potential difference of a cell.
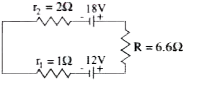
View SolutionFor the given circuit, terminal potential differences of cells are around
View SolutionIf internal resistance of cell is negligible, then current flowing through the circuit is
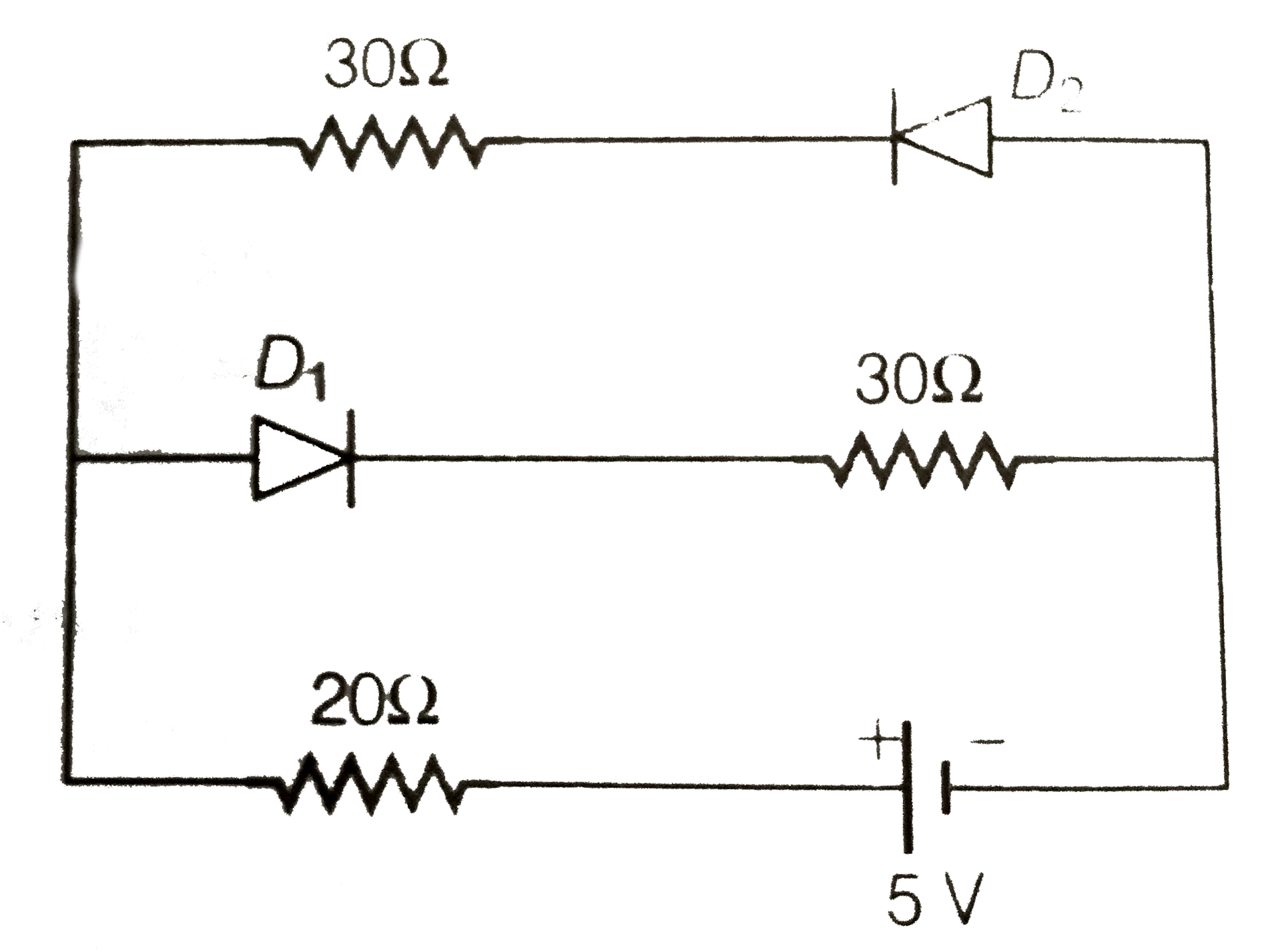
View SolutionState the condition for maximum current to be drawn from the cell.
View SolutionIn the circuit shown, the current drawn by the cell is
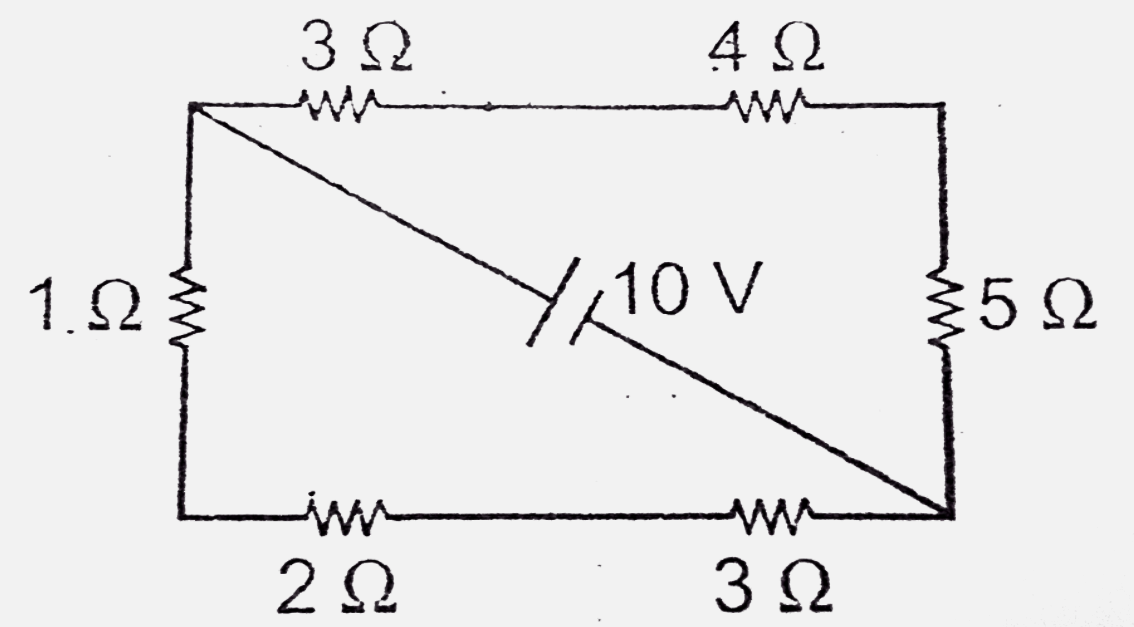
View SolutionWhen capacitor is fully charged, find current drawn from the cell.
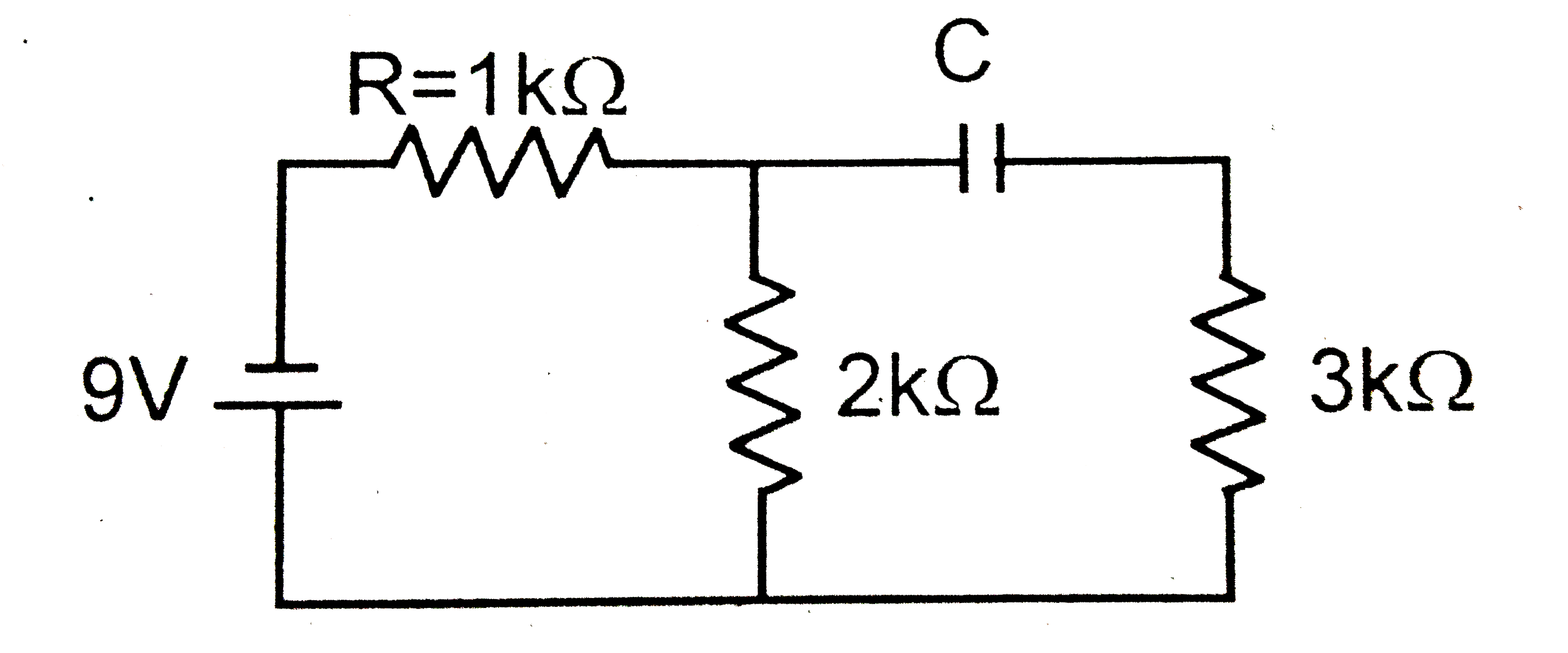
View SolutionWhat transformation of energy takes place when current is drawn from a cell ?
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionA cell of e.m.f. E and internal resistance r is used to send current to an external resistance R. Write expressions for (a) the total resistance of circuit, (b) the current drawn from the cell, (c) the p.d. across the cell, and (d) voltage drop inside the cell.
View Solution
