A series parallel combination battery consisting of a large number N=300 of identical cells, each will an inernal resistance r=0.3Ω, is loaded with an external resistances R=10Ω. Find the number n of parallel groups consisting of an equal number of cells connected in series, at which the external resistance generates the highest thermal power.
A) 2
B) 3
C) 4
D) 6
The correct Answer is:B
To solve the problem, we need to determine the number of parallel groups n that maximizes the thermal power generated in the external resistance R when connected to a series-parallel combination of identical cells.
1. Understanding the Configuration:
- We have N=300 identical cells, each with an internal resistance r=0.3Ω.
- The external resistance is R=10Ω.
- Let x be the number of cells in series in each parallel group. Therefore, the total number of parallel groups is n.
2. Relating Cells in Series and Parallel:
- Since the total number of cells is N, we can express this relationship as:
n⋅x=Norx=Nn
3. Finding the Current:
- For one loop consisting of x cells in series and the external resistance R, using Kirchhoff's loop rule, we can write:
I⋅R+I⋅(x⋅r)=x⋅ϵ
where ϵ is the emf of each cell. Rearranging gives:
I(R+x⋅r)=x⋅ϵ
Thus, the current I can be expressed as:
I=x⋅ϵR+x⋅r
4. Power in the External Resistance:
- The power P dissipated in the external resistance R is given by:
P=I2⋅R
- Substituting for I:
P=(x⋅ϵR+x⋅r)2⋅R
5. Substituting for x:
- Substitute x=Nn:
P=(Nn⋅ϵR+Nn⋅r)2⋅R
- Simplifying gives:
P=(N⋅ϵn⋅R+N⋅r)2⋅R
6. Maximizing Power:
- To find the value of n that maximizes P, we can take the derivative dPdn and set it to zero. This is a more complex calculus step, but we can use the result derived from the theory of maximum power transfer:
n=√N⋅Rr
7. Calculating n:
- Plugging in the values:
n=√300⋅100.3=√10000=100
8. Final Result:
- The number n of parallel groups that maximizes the thermal power in the external resistance is:
n=10
- We have N=300 identical cells, each with an internal resistance r=0.3Ω.
- The external resistance is R=10Ω.
- Let x be the number of cells in series in each parallel group. Therefore, the total number of parallel groups is n.
- Since the total number of cells is N, we can express this relationship as:
n⋅x=Norx=Nn
- For one loop consisting of x cells in series and the external resistance R, using Kirchhoff's loop rule, we can write:
I⋅R+I⋅(x⋅r)=x⋅ϵ
where ϵ is the emf of each cell. Rearranging gives:
I(R+x⋅r)=x⋅ϵ
Thus, the current I can be expressed as:
I=x⋅ϵR+x⋅r
- The power P dissipated in the external resistance R is given by:
P=I2⋅R
- Substituting for I:
P=(x⋅ϵR+x⋅r)2⋅R
- Substitute x=Nn:
P=(Nn⋅ϵR+Nn⋅r)2⋅R
- Simplifying gives:
P=(N⋅ϵn⋅R+N⋅r)2⋅R
- To find the value of n that maximizes P, we can take the derivative dPdn and set it to zero. This is a more complex calculus step, but we can use the result derived from the theory of maximum power transfer:
n=√N⋅Rr
- Plugging in the values:
n=√300⋅100.3=√10000=100
- The number n of parallel groups that maximizes the thermal power in the external resistance is:
n=10
Topper's Solved these Questions
Similar Questions
24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionThree identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionTo get maximum current in a resistance of 3Ω, one can use n parallel rows of m cells each (connected in series). If the total no. of cells is 24 and the internal resistance is 0.5 ohm then
View SolutionUnder what condition will the current in a wire be the same when connected in series and in parallel on n identical cells each having internal resistance r and external resistance R?
View SolutionTwo cell with unequal emfs of 2V and 3V are connected as shown in the figure. If each cell has an internal resistance r = 0.45Ω and external resistance is of 4Ω. Then, Potential drop across resistor 4Ω is
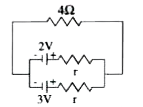
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionA cell of emf 16V and internal resistant 4Ω can deliver maximum power to a load of resistance R where R is equal to
View SolutionTwo identical cells each of emf ε, having negligible internal reistance r, are connercted in parallel with each other across an external resistance R. What is the current through this resistance.
View Solution
