If light passes near a massive object, the gravitational interation causes a bending of the ray. This can be thought of as heappening due to a change in the effective refrative index of the medium given by
n(r)=1+2GM/rc2
where r is the distance of the point of consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in vacuum.
Considering a spherical object find the deviation of the ray form the original path as it graxes the object. Solution in Gujrati

⇒ As shown in the figure , when light ray passes tangentially to the surface of central massive body of mass M and radius R , suppose it gets deviated by amount dθ within distacen dr.
⇒ Now, applying Snell.s law at the point where light ray is made incident on the concentric spherical suface at distance, r, from the centre of central massive body we get ,
nsinθ=(n+dn)sin(θ+dθ)
∴nsinθ=(n+dn)(sinθcosdθ+cosθsindθ)
∴nsinθ=nsinθcos(dθ)+ncos(dθ)+ncosθsin(dθ)+(dn)sinθcos(dθ)+(dn)cosθsin(dθ)
⇒ Since dthη is extremely small, we can take sin(dθ)=(dθ)
and taking cos(θ)=
nsinθ=nsinθ+ncosθ(dθ)+(dh)sinθ+(dn)cosθ(dθ)
∴0=ncosθ(∵(dn)(cosθ)(dthη is negligible)
∴−(dn)sinθ=ncosθ(dθ)
∴−(dndr)sinθ=ncosθ(dθdr)
∴−(dndr)tanθ=n(dθdr).....(1)
⇒ From the statement ,
n=1+2GMrc2
∴dndr=0+2GMc2(−1r2)[∵ddr(1r)=−1r2]
∴dndr=0+2GMr2c2 ......(2)
⇒ From equation (1) and (2) ,
2GMr2c2tanθ=(1+2GMrc2)dθdr
⇒ Here inside the backet on R.H.S
2GMrc2<<<<1 and so neglecing it,
2GMr2c2tanθ=dθdr
∴dθ=2GMc2(tanθr2)dr.......(3)
⇒ From the figure r2=x2+R2 .......(4)
∴2rdr=2xdx+0
∴rdr=xdx⇒dr=xdxr ......(5)
⇒ From equations (3) and (5),
dθ=2GMc2tanθr3xdx......(7)
⇒ Here,
r2=x2+R2
∴(r2)3/2=(x2+R2)3/2
∴r3=(x2+R2)3/2 ......(8)
⇒ From equaitons (6),(7) and (8),
dθ=2GMc2R(x2+R2)3/2dx.....(9)
⇒ Now suppose,
x=Rtanθϕ
∴dx=Rsec2ϕdϕ .......(11)
⇒ Now,
(x2+R2)3/2=(R2tan2ϕ+R2)3/2
=(R2sec2ϕ)3/2
=R3sec3ϕ ........(12)
⇒ From equaitons (9),(11),(12),
dθ=2GMRc2cosϕ d ϕ.......(13)
⇒ From equation (10), if
x=−∞ then ϕ=−π2 rad
x=+∞ then ϕ=lπ2 rad
⇒ Also when x=−∞,θ=0
x=+∞,θ−θ0
Taking intergration on both the sides of eqation (13),
∫θ00dθ=2GMRc2∫+π2−π2cosθ d θ
∴θ0=2GMRc2{sinϕ}+π2−π2
=2GMRc2{sin(π2)−sin(−π2)}
∴θ0=4GMRc2
⇒ Above equation gives required result.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-D (MULTIPLE CHOICE QUESTIONS (MCQs))(MCQs FROM .DARPAN. BASED ON TEXTBOOK)
26 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-D (MULTIPLE CHOICE QUESTIONS (MCQs))(MCQs FROM .DARPAN. BASED ON TEXTBOOK)(REFRACTION)
32 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-C (NCERT EXEMPLAR SOLUTION) (SHORT ANSWER TYPE QUESITONS)
6 Videos
- MOVING CHARGES AND MAGNETISMBOOK - KUMAR PRAKASHANCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - SECTION D (MCQs ASKED IN COMPETITIVE EXAMS)
34 Videos
- SAMPLE QUESTION PAPER BOOK - KUMAR PRAKASHANCHAPTER - SAMPLE QUESTION PAPER EXERCISE - PART-B SECTION-C
5 Videos
Similar Questions
Diameter of spherical mirror is 10 cm, what will be aperture of mirror ?
View SolutionRefraction index of medium-2 with respect to medium-1 is ...... .
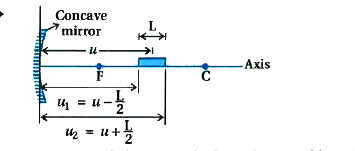
View SolutionA short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image ? You may take L<<|v−f|.
View SolutionElectric charge Q having mass M moves on a circular path of radius R with velocity →v, perpendicular to uniform magnetic field B. When a particle completes one revolution, work done by the field is _______
View SolutionTwo charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1 .
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
View SolutionGravtational potential at a distance 'r' from a point mass 'm' is V = -(GM)/(r) Find gravitational field strength at that point.
View SolutionTwo bodies of masses M_(1) and M_(2) , are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
View SolutionIf light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by n( r) = 1+ 2 GM//rc^2 where r is the distance of the point consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in vacuum. Considering a spherical object, find the deviation of the ray from the original path as it grazes the object.
View SolutionA massive object in space causes gravitational lensing. Light from a distant source gets deflected by a massive lensing object. This was first observed in 1919 and supported Einstein’s general theory of relativity. The angle theta by which light gets deflected due to a massive body depends on the mass (M) of the body, universal gravitational constant (G), speed of light (c) and the least distance (r) between the lensing object and the apparent path of light. Derive a formula for theta using method of dimensions. Make suitable assumptions.
View SolutionA massive black hole of mass m and radius R is spinning with angular velocity omega . The power P radiated by it as gravitational waves is given by P = Gc^(–5)m^(x)R^(y)omega^(z) , where c and G are speed of light in free space, and the universal gravitational constant , respectively. Then
View SolutionThe acceleration due to gravity'g' for objects on or near the surface of earth is related to the universal gravitational constant 'G' as ('M' is the mass of the earth and 'R' is its radius):
View Solutionपृथ्वी की सतह पर अथवा उसके निकट वस्तुओ के लिए गुरुत्वीय त्वरण g , सार्वत्रिक गुरुत्वीय स्थिरांक G से किस प्रकार संबंधित है? (M पृथ्वी का द्रव्यमान और R इसकी त्रिज्या है)
View SolutionTwo bodies of masses m and 9m are placed at a distance 'r'.The gravitational potential at a point on the line joining them where gravitational field is zero is (G is universal gravitational constant)
View SolutionIf light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by n( r) = 1+ 2 GM//rc^2 where r is the distance of the point consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in vacuum. Considering a spherical object, find the deviation of the ray from the original path as it grazes the object.
View SolutionTwo bodies of masses .m. and .9m. are placed at a distance .r.. The gravitational potential at a point on the line joining them, where gravitational field is zero, is (G is universal gravitational constant )
View Solution
