If the flux of the electric field through a closed surface is zero,
the electric field must be zero everywhere on the surface
the electric field may be zero everywhere on the surface
the charge inside the surface must be zero
the charge in the vicinity of the surface must be zero.
The correct Answer is:B, C
To solve the question, we need to analyze the implications of the electric flux being zero through a closed surface according to Gauss's Law.
1. Understanding Electric Flux:
Electric flux (Φ) through a closed surface is defined by Gauss's Law as:
Φ=∮E⋅dA=Qencϵ0
where E is the electric field, dA is the differential area vector, Qenc is the charge enclosed by the surface, and ϵ0 is the permittivity of free space.
2. Given Condition:
The problem states that the electric flux through the closed surface is zero:
Φ=0
3. Applying Gauss's Law:
From Gauss's Law, if the electric flux is zero, we can write:
Qencϵ0=0
This implies that:
Qenc=0
Therefore, the total charge enclosed by the surface must be zero.
4. Implications for Electric Field:
The electric field E can be zero everywhere on the surface, but it is not necessarily true that it must be zero everywhere. For example, if there are equal amounts of positive and negative charges outside the surface, they can create an electric field that cancels out at the surface, resulting in zero net flux.
5. Conclusion:
- The electric field may be zero everywhere on the surface (Option B).
- The charge inside the surface must be zero (Option C).
- However, the electric field does not have to be zero everywhere; it can exist due to external charges.
Final Answer:
The correct options are:
- B: The electric field may be zero everywhere on the surface.
- C: The charge inside the surface must be zero.
Electric flux (Φ) through a closed surface is defined by Gauss's Law as:
Φ=∮E⋅dA=Qencϵ0
where E is the electric field, dA is the differential area vector, Qenc is the charge enclosed by the surface, and ϵ0 is the permittivity of free space.
The problem states that the electric flux through the closed surface is zero:
Φ=0
From Gauss's Law, if the electric flux is zero, we can write:
Qencϵ0=0
This implies that:
Qenc=0
Therefore, the total charge enclosed by the surface must be zero.
The electric field E can be zero everywhere on the surface, but it is not necessarily true that it must be zero everywhere. For example, if there are equal amounts of positive and negative charges outside the surface, they can create an electric field that cancels out at the surface, resulting in zero net flux.
- The electric field may be zero everywhere on the surface (Option B).
- The charge inside the surface must be zero (Option C).
- However, the electric field does not have to be zero everywhere; it can exist due to external charges.
The correct options are:
- B: The electric field may be zero everywhere on the surface.
- C: The charge inside the surface must be zero.
Topper's Solved these Questions
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Exercises
24 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 1
6 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
Similar Questions
Figure shown a closed surface which intersects a conducting sphere. If a positive charge is placed at the point P, the flux of the electric field through the closed surface

View SolutionFigure shown a closed surfce which intersects a conducting sphere. If a positive charge is placed at the point P, the flux of the electric field through the closed surface

View SolutionA capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
View SolutionFigure shows four charges q1,q2,q3,andq4 fixed is space. Then the total flux of the electric field through a closed surface S, due to all the charges, is

View SolutionA Gaussian surface in the cylinder of cross-section πa2 and length L is immersed in a uniform electric field E with the cylinder axis parallel to the field. The flux ϕ of the electric field through the closed surface is
View SolutionAn imaginary closed surface P is constructed around a neutral conducting wire connected to a battery and a switch as shown in figure. As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface P is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface :
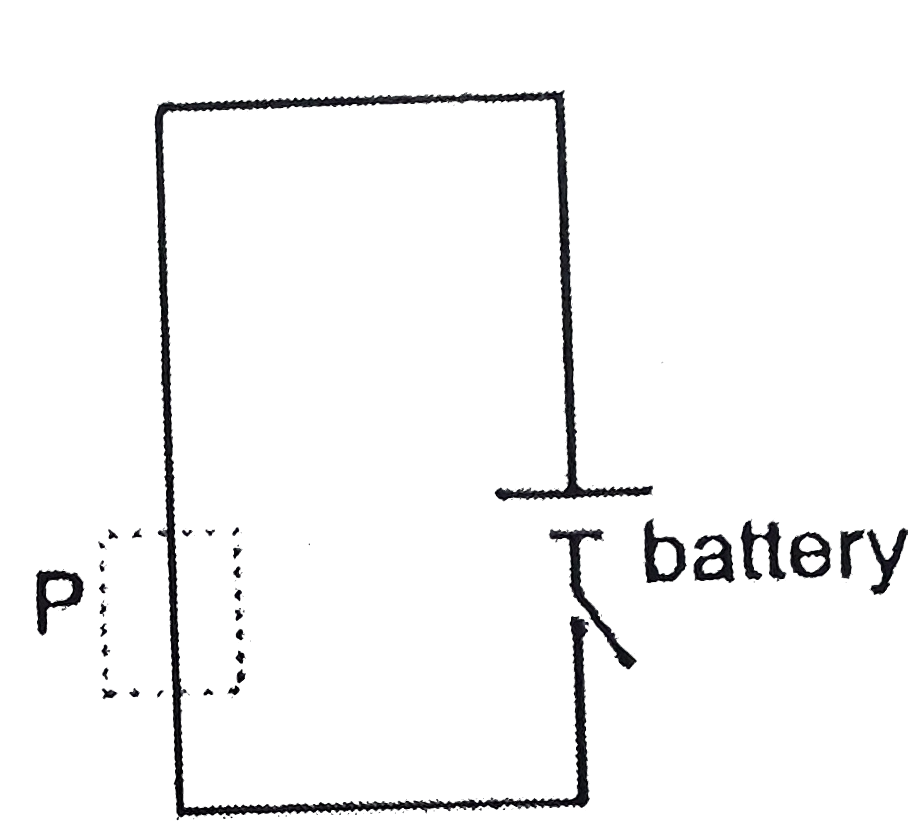
View SolutionA closed surface S is constructed around a conducting wire connected to a battery and a switch (figure 30-Q6). As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface S is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface

View SolutionFind the flux of the electric field through each of the five surfaces of the inclined plane as shown in figure. What is the total flux through the entire closed surface?

View SolutionA capacitor of capacitance C is connected to a cell of emf V and when fully charged, it is disconnected. Now the separation between the plates is doubled. The change in flux of electric field through a closed surface enclosing the capacitor is
View SolutionElectric charge are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10cm surrounding the total charge is 25 V m. The flux over a concentric sphere of radius 20 cm will be
View Solution
