If the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficient so that a scooter going at 18km/h does not skid?
The correct Answer is:B
To solve the problem of finding the minimum friction coefficient required for a scooter to make a turn without skidding on a horizontal road, we can follow these steps:
1. Convert the Speed from km/h to m/s:
The speed of the scooter is given as 18km/h. To convert this to meters per second (m/s), we use the conversion factor:
1km/h=518m/s
Therefore,
v=18km/h×518=5m/s
2. Identify the Forces Acting on the Scooter:
When the scooter is turning, the centripetal force required to keep it moving in a circular path is provided by the frictional force. The frictional force can be expressed as:
Ffriction=μ⋅N
where μ is the coefficient of friction and N is the normal force. On a horizontal road, the normal force N equals the weight of the scooter:
N=mg
where m is the mass of the scooter and g is the acceleration due to gravity (approximately 10m/s2).
3. Set Up the Equation for Centripetal Force:
The centripetal force required to keep the scooter in circular motion is given by:
Fcentripetal=mv2r
where r is the radius of the turn.
4. Equate the Forces:
For the scooter to not skid, the frictional force must be equal to the centripetal force:
μmg=mv2r
5. Cancel the Mass m:
Since m appears on both sides of the equation, we can cancel it out:
μg=v2r
6. Solve for the Coefficient of Friction μ:
Rearranging the equation gives:
μ=v2gr
7. Substitute the Values:
We know:
- v=5m/s
- g=10m/s2
- Assume a radius r (for example, r=10m for calculation purposes):
μ=(5)210⋅10=25100=0.25
Final Answer:
The minimum coefficient of friction required for the scooter to not skid while turning is μ=0.25.
The speed of the scooter is given as 18km/h. To convert this to meters per second (m/s), we use the conversion factor:
1km/h=518m/s
Therefore,
v=18km/h×518=5m/s
When the scooter is turning, the centripetal force required to keep it moving in a circular path is provided by the frictional force. The frictional force can be expressed as:
Ffriction=μ⋅N
where μ is the coefficient of friction and N is the normal force. On a horizontal road, the normal force N equals the weight of the scooter:
N=mg
where m is the mass of the scooter and g is the acceleration due to gravity (approximately 10m/s2).
The centripetal force required to keep the scooter in circular motion is given by:
Fcentripetal=mv2r
where r is the radius of the turn.
For the scooter to not skid, the frictional force must be equal to the centripetal force:
μmg=mv2r
Since m appears on both sides of the equation, we can cancel it out:
μg=v2r
Rearranging the equation gives:
μ=v2gr
We know:
- v=5m/s
- g=10m/s2
- Assume a radius r (for example, r=10m for calculation purposes):
μ=(5)210⋅10=25100=0.25
The minimum coefficient of friction required for the scooter to not skid while turning is μ=0.25.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.3
4 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Assertion And Reason
28 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.1
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
If the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficeint so that a scooter going at 18 km/hr does not skid?
View SolutionIf the road is horizontal (no banking), what should be the minimum friction coefficeint so that a scooter going at 18 km/hr does not skid for r=10m ?
View Solution
Knowledge Check
A 4m long ladder weighing 25kg rests with its upper end against a smooth wall and lower end on rough ground.What should be the minimum coefficient of friction between the ground and the ladder for it to be inclined at 60∘ with the horizontal without slipping? (Takeg=10m/s2)
Aa. 0.19Bb. 0.29Cc. 0.39Dd. 0.49
Block M slides down on frictionless incline as shown. The minimum friction coefficient so that m does not slide with respect to M would be :
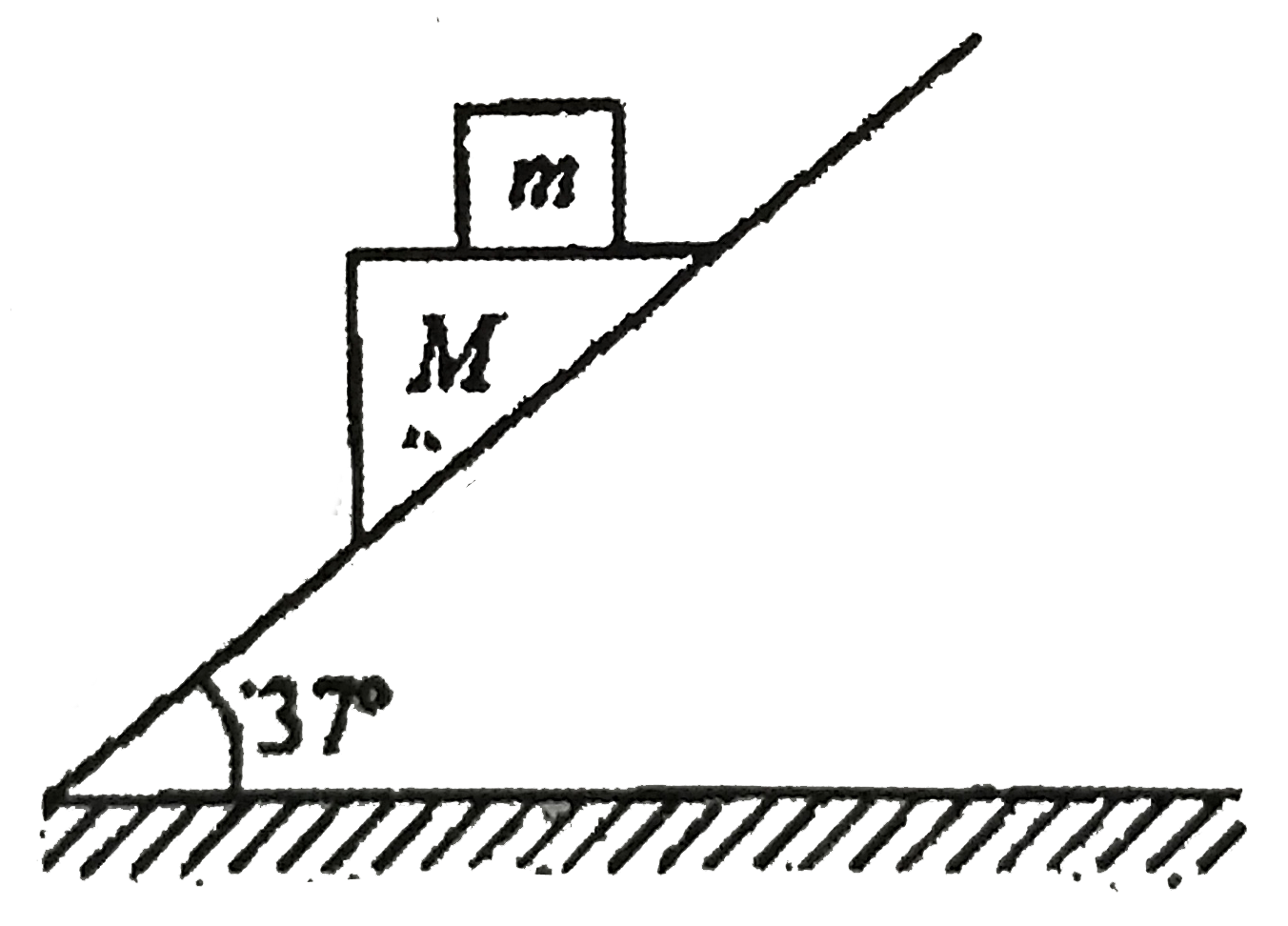
View SolutionA sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
View SolutionA sphere of mass m rolls without slipping on an inclined plane of inclination θ. Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?
View SolutionA track consists of two circular pars ABC and CDE of equal radius 100 m and joined smoothly as shown in figure.Each part subtends a right angle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Find the normal contact force by the road on the cycle when it is at B and at D. b.Find the force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between the road and the cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g=10ms2

View SolutionA car goes on a circular horizontal road of radius 100 m. What should be the minimum coefficient of friction between the tyres and the road so that it completes the circle with velocity 10 m/s without slipping ? (Take g=10m/s2)
View SolutionA block of mass is kept on an inclined plane of a lift moving down with acceleration of 2ms−2 What should be the minimum coefficient of friction to let the block move down with constant velocity?

View SolutionThe length of a uniform ladder of mass m is 1. It leans against a smooth wall making an angle θ with the horizontal. What should be the force of friction between the floor and ladder so that the ladder does not slip ?
View Solution
