If two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
√3Gm22r2
√3Gm2r2
Gm2r2
Gm22r2
The correct Answer is:B
Gravitational force on particle at A C due to particle at A is
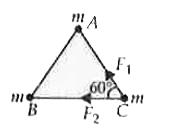
F1=Gmmr2=Gm2r2 along CA
Gravitational force on particle at C due to particle at B is
F2=Gm2r2 along CB
As →F1 and →F2 are inclined at an angle 60∘ , so the resultant gravitational force on particle at C is
F=√F21+F22+2F1F2cos60∘
=√F21+F21+2F1×F1×12=√3F1=√3Gm2r2 (∵F1=F2)
Topper's Solved these Questions
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)
19 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)
6 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)
9 Videos
- BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYBOOK - MTG GUIDECHAPTER - BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYEXERCISE - AIPMT / NEET (MCQs)
11 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
Similar Questions
If two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the
(a) the mid point of a side
(b) centre of the triangle
View Solution
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−2√2GmlB−3√2GmlC−2GmlD−4√2GmlThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
A−3Gm22bB−Gm22bC−3Gm2bD−Gm2bThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
A−3GMLB−√3GMLC−3√3GMLD−GM3√3L
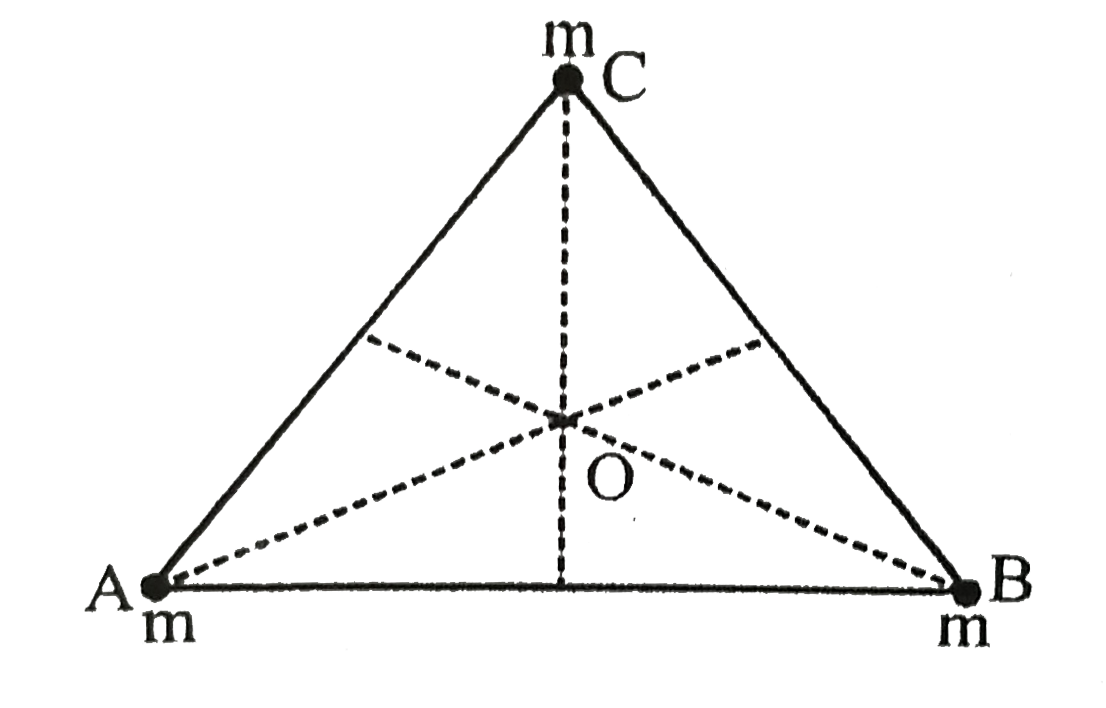
Three particles, each of mass m are placed at the vertices of an equilateral triangle of side a. What are the gravitation field and gravitational potential at the centroid of the triangle.
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionTwo charge +Q,−Q are placed at the two verticels of an equilateral triangle of side 'a'. Then the intensity of electric field at the third vertex is
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View Solution
