In a carbon monoxide molecule, the carbon and the oxygen atoms are separated by a distance 1.2×10−10m. The distance of the centre of mass from the carbon atom is
(a) 0.48×10−10m
(b) 0.51×10−10m
(c) 0.74×10−10m
(d) 0.68×10−10m
The correct Answer is:D
To find the distance of the center of mass from the carbon atom in a carbon monoxide (CO) molecule, we can follow these steps:
1. Identify the masses of the atoms:
- Let the mass of the carbon atom (m_C) be 12 atomic mass units (u).
- Let the mass of the oxygen atom (m_O) be 16 atomic mass units (u).
2. Define the distance between the atoms:
- The distance (d) between the carbon and oxygen atoms is given as d=1.2×10−10 m.
3. Set up the equation for the center of mass:
- The center of mass (CM) of a two-particle system can be calculated using the formula:
xCM=mC⋅xC+mO⋅xOmC+mO
- For our case, we can assume the carbon atom is at position 0 (x_C = 0) and the oxygen atom is at position d (x_O = d). Thus, the equation simplifies to:
xCM=mC⋅0+mO⋅dmC+mO=mO⋅dmC+mO
4. Substitute the values:
- Substitute the masses and distance into the equation:
xCM=16⋅(1.2×10−10)12+16
5. Calculate the denominator:
- The total mass is:
12+16=28
6. Calculate the center of mass:
- Now substitute the values into the equation:
xCM=16⋅(1.2×10−10)28
7. Perform the multiplication:
- Calculate 16⋅(1.2×10−10):
16⋅1.2=19.2
- Thus, we have:
xCM=19.2×10−1028
8. Perform the division:
- Now divide 19.2 by 28:
xCM≈0.6857×10−10 m
9. Final answer:
- Rounding to two decimal places, we get:
xCM≈0.68×10−10 m
Conclusion:
The distance of the center of mass from the carbon atom is approximately 0.68×10−10 m.
- Let the mass of the carbon atom (m_C) be 12 atomic mass units (u).
- Let the mass of the oxygen atom (m_O) be 16 atomic mass units (u).
- The distance (d) between the carbon and oxygen atoms is given as d=1.2×10−10 m.
- The center of mass (CM) of a two-particle system can be calculated using the formula:
xCM=mC⋅xC+mO⋅xOmC+mO
- For our case, we can assume the carbon atom is at position 0 (x_C = 0) and the oxygen atom is at position d (x_O = d). Thus, the equation simplifies to:
xCM=mC⋅0+mO⋅dmC+mO=mO⋅dmC+mO
- Substitute the masses and distance into the equation:
xCM=16⋅(1.2×10−10)12+16
- The total mass is:
12+16=28
- Now substitute the values into the equation:
xCM=16⋅(1.2×10−10)28
- Calculate 16⋅(1.2×10−10):
16⋅1.2=19.2
- Thus, we have:
xCM=19.2×10−1028
- Now divide 19.2 by 28:
xCM≈0.6857×10−10 m
- Rounding to two decimal places, we get:
xCM≈0.68×10−10 m
The distance of the center of mass from the carbon atom is approximately 0.68×10−10 m.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective
32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
In a carbon monoxide molecule, the carbon and the oxygen atoms are separted by a distance 1.12×10−10 m. The distance of the centre of mass from the carbon atom is
A. 0.64×10−10m
B. 0.56×10−6m
C. 0.51×10−10m
D. 0.48×10−10 m
View SolutionIn acetylene molecule, the carbon atoms are linked by:
View Solution
Knowledge Check
One requires 11eV of energy to dissociate a carbon monoxide molecule into carbon and oxygen atoms. The minimum frequency of the appropriate electromagnetic radiation to achieve the dissociation lies in.
Avisible regionBinfrared regionCultraviolet regionDmicrowave region
In the formation of ethylene molecule , the carbon atom makes use of
View SolutionWhich molecules have sp3 carbon atoms :
View SolutionThe distance between the centres of carbon and oxygen atoms in the carbon monoxide molecule is 1.130Å . Locate the centre of mass of the molecule relative to the carbon atom .
View SolutionThe distance between the carbon atom and the oxygen atom in a carbon monoxide molecule is 1.1Å. Given, mass of carbon atom is 12 a.m.u. and mass of oxygen atom is 16 a.m.u., calculate the position of the centre of mass of the carbon monoxide molecule
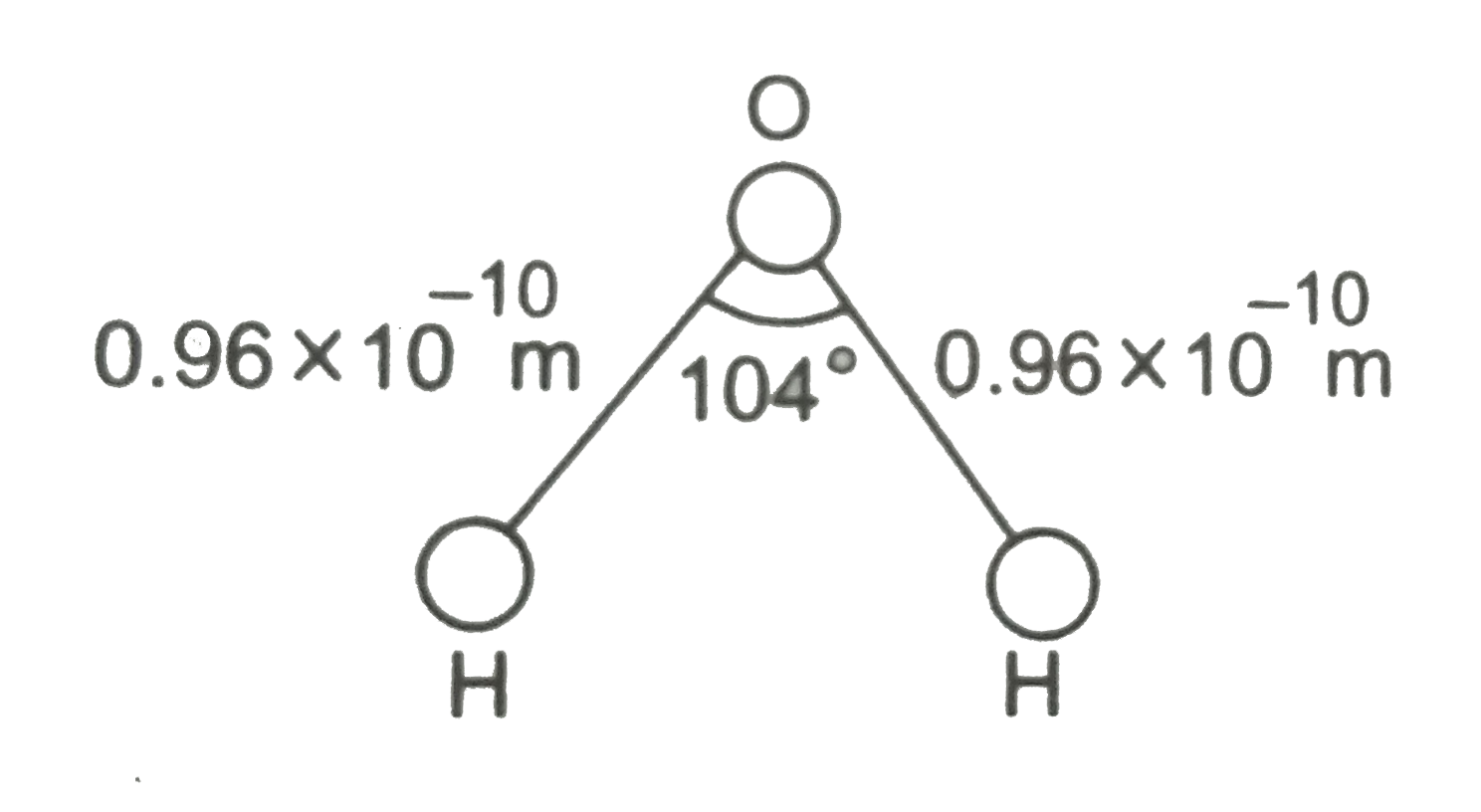
View SolutionThe structure of a water molecule is shown in figure. Find the distance of the distance of the centre of mass of the molecule from the centre of the oxygen atom.
View SolutionOne requires 11eV of energy to dissociate a carbon monoxide molecule into carbon and oxygen atoms. The minimum frequency of the appropriate electromagnetic radiation to achieve the dissociation lies in.
View SolutionOne requires 11eV of energy to dissociate a carbon monoxide molecule into carbon and oxygen atoms. The minimum frequency of the appropriate electromagnetic radiation to achieve the dissociation lies in.
View Solution
