In a double slit pattern (λ=6000Å) the first order and tength order maxima fall at 12.50 mm and 14.75mm from a particular reference point. If λ is changed to 5500Å then find the position of zero order and tenth order fringes, othe
Distance between 10 fringes is
9β=(14.75−12.50)mm=2.25mm
∴ Fringe width β=0.25mm
As fringe width ∝λ
When the wavelength is changed from 6000Å to 5500Å then the new fringe width will become
β'=(55006000)β=(55006000)(0.25)
β'=0.23mm
The produce of central for zero order maxima will remain unchanged Earlier it was at a position
y0=y1=β
=12.50−0.25=12.25mm
The new position of tength order maxima will be
y10=y0+10β'
=12.25+(10)(0.23)=14.55mm
Topper's Solved these Questions
Similar Questions
In a double slit pattern (λ=6000Å), the first order and tenth order maxima fall at 12.50 mm and 14.75mm from a particular reference point. If λ is changed to 5500Å, find the position of zero order and tenth order fringes, other arrangements remaining the same.
View SolutionIn a double slit pattern (λ=6000Å), the first order and tenth order maxima fall at 12.50 mm and 14.75mm from a particular reference point. If λ is changed to 5500Å, find the position of zero order and tenth order fringes, other arrangements remaining the same.
View SolutionA parallel beam of light of all wavelength greater than 3000Å falls on a double slit in a Young's double slit experiment. It is observed that the wavelength 3600Å and 6000Å are absent at a distance of 31.5 mm from the position of the centre maximum and the orders of the interference at this point for the two wavelength differ by 7. If the distance between the slit and the screen in 1m, the separation between the two slits is
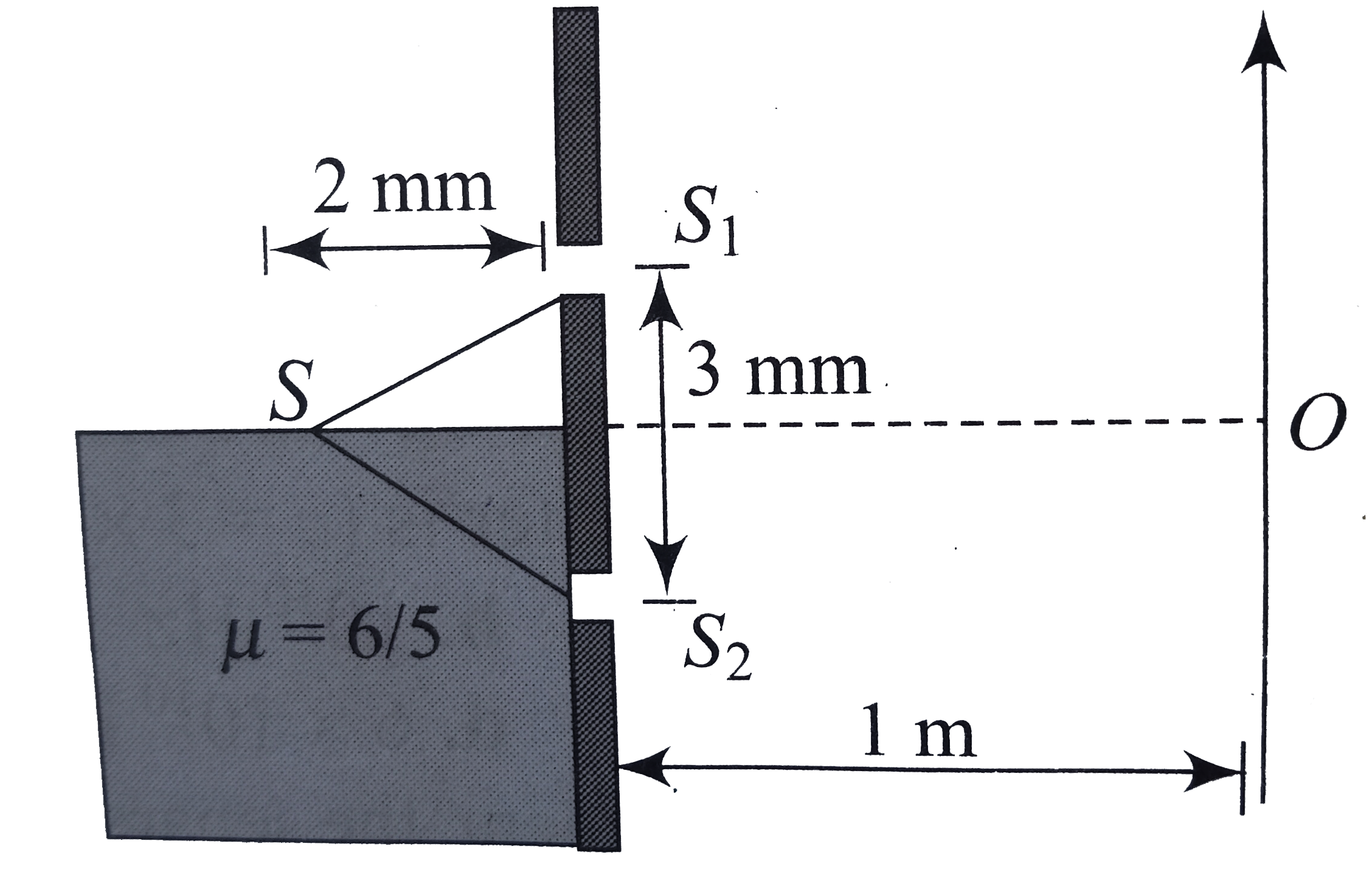
View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distacne from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
 View Solution
View SolutionLight of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View SolutionIn Young's double slit experiment the fringes are fomred at a distance of 1 m from double slit of separation 0.12 mm calculate.
(i). The distance of 3rd dark band from the centre of the screen.
(ii). The distance of 3rd bright band from the centre of the screen, Given λ=6000ÅView SolutionIn a double slit experiment, the distance between the slits is 5.0 mm and the slits are 1.0m from the screen. Two interference patterns can be seen on the screen one due to light with wavelength 480nm, and the other due to light with wavelength 600nm. What is the separation on the screen between the third order bright fringes of the two intergerence patterns?
View SolutionIn Young's experiment, light of wavelength 600 nm falls on the double slits separated by 0.1 mm. What is the highest order of maximum intensity in the interference pattern obtained on a screen kept 3 m from the slits? How does the highest order change if the distance of screen from the slits is changed?
View SolutionA Lloyd's mirror or length 5 cm is illuminated with monochromatic light of wavelength λ(=6000Å) from a narrow 1 mm slit in its plane and 5 cm plane from its near edge. Find the fringe width on a screen 120 cm from the slit and width of interference pattern on the screen.
 View Solution
View SolutionCoherent light with wavelength 600nm passes through two very narrow slits and the interference pattern is observed on a screen 3.00 m from the slits. The first order bright fringe is at 4.94 mm from the centre of the central bright fringe. For what wavelength of light will the first order dark fringe be observed at this same point on the screen?
View Solution

