In a free space, a thin rod carrying uniformly distributed negative charge −q is placed symmetrically along the axis of a tin ring of radius R varrying uniformly dostributed charge Q. The mass of the rod is m and length is l=2R. The ring is fixed and the rod is free to move. The rod is displaced slightly along the axis of the ring and then released. Find the period T to the small amplitude oscillations of the rod.
To solve the problem of finding the period T of small amplitude oscillations of a charged rod placed along the axis of a charged ring, we can follow these steps:
Step 1: Understand the System
We have a thin rod of length l=2R carrying a uniformly distributed negative charge −q. The rod is placed symmetrically along the axis of a fixed tin ring of radius R that carries a uniformly distributed positive charge Q. The rod is free to move along the axis of the ring.
Step 2: Displacement and Forces
When the rod is slightly displaced by a distance y along the axis, it experiences a restoring force due to the electric field created by the charged ring. The electric field E at a distance x from the center of the ring along its axis is given by:
E=kQx(x2+R2)3/2
where k=14πϵ0.
Step 3: Calculate the Electric Field at Displacement
For small displacements, we can approximate x as R (since y is small compared to R):
E≈kQR(R2+R2)3/2=kQR(2R2)3/2=kQR2√2R3=kQ2√2R2
Step 4: Calculate the Force on the Rod
The force F acting on the rod due to the electric field is:
F=−qE
Substituting the expression for E:
F=−q(kQ2√2R2)
This force acts to restore the rod to its equilibrium position.
Step 5: Relate Force to Acceleration
Using Newton's second law, we can express the force as:
F=ma
where a is the acceleration of the rod. For small oscillations, we can relate the force to the displacement y:
ma=−kqQ2√2R2⇒a=−kqQ2√2mR2y
Step 6: Identify the Oscillation Type
This is a simple harmonic motion (SHM) equation of the form:
a=−ω2y
where ω2=kqQ2√2mR2.
Step 7: Find the Period of Oscillation
The period T of SHM is given by:
T=2π√mkeff
where keff=kqQ2√2R2. Therefore:
T=2π√m⋅2√2R2kqQ
Final Expression for the Period
Thus, the period T of small amplitude oscillations of the rod is:
T=2π√2√2mR2kqQ
We have a thin rod of length l=2R carrying a uniformly distributed negative charge −q. The rod is placed symmetrically along the axis of a fixed tin ring of radius R that carries a uniformly distributed positive charge Q. The rod is free to move along the axis of the ring.
When the rod is slightly displaced by a distance y along the axis, it experiences a restoring force due to the electric field created by the charged ring. The electric field E at a distance x from the center of the ring along its axis is given by:
E=kQx(x2+R2)3/2
where k=14πϵ0.
For small displacements, we can approximate x as R (since y is small compared to R):
E≈kQR(R2+R2)3/2=kQR(2R2)3/2=kQR2√2R3=kQ2√2R2
The force F acting on the rod due to the electric field is:
F=−qE
Substituting the expression for E:
F=−q(kQ2√2R2)
This force acts to restore the rod to its equilibrium position.
Using Newton's second law, we can express the force as:
F=ma
where a is the acceleration of the rod. For small oscillations, we can relate the force to the displacement y:
ma=−kqQ2√2R2⇒a=−kqQ2√2mR2y
This is a simple harmonic motion (SHM) equation of the form:
a=−ω2y
where ω2=kqQ2√2mR2.
The period T of SHM is given by:
T=2π√mkeff
where keff=kqQ2√2R2. Therefore:
T=2π√m⋅2√2R2kqQ
Thus, the period T of small amplitude oscillations of the rod is:
T=2π√2√2mR2kqQ
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionA nonconducting ring of radius R has uniformly distributed positive charge Q. A small part of the ring.of length d, is removed (d<<R). The electric field at the centre of the ring will now be
View SolutionA short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

The net force acting on the dipole will be
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a simple harmonic motion along the axis of the ring. State True or False.
View Solutiontwo identical rings of radius R have uniformly distributed charge Q(Q>0) each. Both the rings are fixed and are placed coaxially separated by a distance of R. if a small positive point charge is placed at the mid point and is displaced slightly along the axis then,
View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.

View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionThe ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
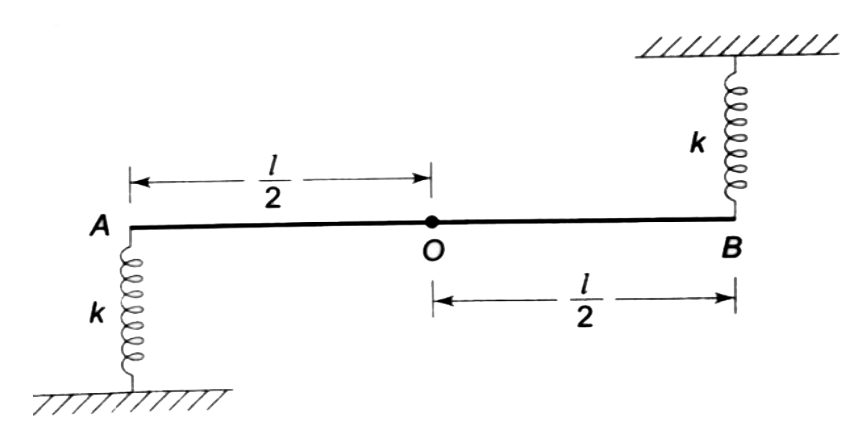
View SolutionA ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View Solution
