In a soccer practice sesson of the football is kept at the centre of the field 40 yards from the 10 ft hight goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at angle of 450 to the horizontal. Will the ball reach the goal post?
The correct Answer is:A, B, C
To determine if the football will reach the goal post, we need to analyze the projectile motion of the ball. Here’s a step-by-step solution:
Step 1: Convert the distance to feet
The distance from the football to the goal post is given as 40 yards. We need to convert this distance into feet:
- Conversion: 1 yard = 3 feet
- Calculation: 40 yards = 40 × 3 = 120 feet
Step 2: Break down the initial velocity into components
The football is kicked at a speed of 64 ft/s at an angle of 45 degrees. We need to find the horizontal (x) and vertical (y) components of the initial velocity:
- Horizontal component (u_x):
ux=u⋅cos(45∘)=64⋅1√2=64√2≈45.25 ft/s
- Vertical component (u_y):
uy=u⋅sin(45∘)=64⋅1√2=64√2≈45.25 ft/s
Step 3: Calculate the time of flight to reach the goal post
Using the horizontal motion equation, we can find the time (t) it takes for the ball to travel 120 feet:
- Horizontal motion equation:
x=ux⋅t
- Rearranging for time:
t=xux=12045.25≈2.65 seconds
Step 4: Calculate the height of the ball at time t
Now we need to find out how high the ball will be after 2.65 seconds using the vertical motion equation:
- Vertical motion equation:
y=uy⋅t−12gt2
where g (acceleration due to gravity) is approximately 32.2 ft/s².
- Substituting the values:
y=45.25⋅2.65−12⋅32.2⋅(2.65)2
- Calculate:
y≈120.86−0.5⋅32.2⋅7.0225
y≈120.86−113.59≈7.27 feet
Step 5: Compare the height with the goal post height
The height of the goal post is 10 feet. The calculated height of the ball when it reaches the goal post is approximately 7.27 feet.
Conclusion
Since the height of the ball (7.27 feet) is less than the height of the goal post (10 feet), the ball will not reach the goal post.
---
The distance from the football to the goal post is given as 40 yards. We need to convert this distance into feet:
- Conversion: 1 yard = 3 feet
- Calculation: 40 yards = 40 × 3 = 120 feet
The football is kicked at a speed of 64 ft/s at an angle of 45 degrees. We need to find the horizontal (x) and vertical (y) components of the initial velocity:
- Horizontal component (u_x):
ux=u⋅cos(45∘)=64⋅1√2=64√2≈45.25 ft/s
- Vertical component (u_y):
uy=u⋅sin(45∘)=64⋅1√2=64√2≈45.25 ft/s
Using the horizontal motion equation, we can find the time (t) it takes for the ball to travel 120 feet:
- Horizontal motion equation:
x=ux⋅t
- Rearranging for time:
t=xux=12045.25≈2.65 seconds
Now we need to find out how high the ball will be after 2.65 seconds using the vertical motion equation:
- Vertical motion equation:
y=uy⋅t−12gt2
where g (acceleration due to gravity) is approximately 32.2 ft/s².
- Substituting the values:
y=45.25⋅2.65−12⋅32.2⋅(2.65)2
- Calculate:
y≈120.86−0.5⋅32.2⋅7.0225
y≈120.86−113.59≈7.27 feet
The height of the goal post is 10 feet. The calculated height of the ball when it reaches the goal post is approximately 7.27 feet.
Since the height of the ball (7.27 feet) is less than the height of the goal post (10 feet), the ball will not reach the goal post.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective 2
10 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
Similar Questions
A ball is thrown at a speed of 40 m/s at an angle of 600 with the horizontal. Find a. the maximum height reached and b. the range of te ball. Take g=10ms2.
View SolutionA ball is thrown from a field with a speed of 12.0 m/s at an angle of 450 with the horizontal. At what distance will it hit the field again ? Take g=10.0ms2
View Solution
Knowledge Check
An effective tactic in tennis, when your opponent is near the net, consists of lofting the ball over his head, forcing him to move quickly away from the net (see figure). Suppose that you loft the ball with an initial speed of 15.0 m/s, at an angle of 50.0∘ above the horizontal. At this instant your opponent is 10.0 m away from the ball. He begins moving away from you 0.30 s later, hoping to reach the ball and hit it back at the moment that it is 2.10 m above its launch point. With what minimum average speed must he move? (Ignore the fact that he can stretch, so that his racket can reach the ball before he does.)
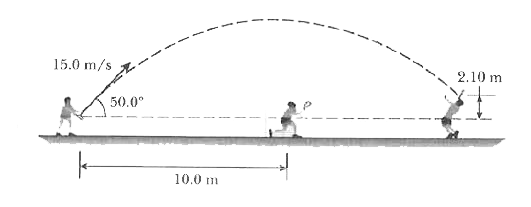 A4.98 m/sB5.79 m/sC5.14 m/sD9.64 m/s
A4.98 m/sB5.79 m/sC5.14 m/sD9.64 m/sIn a football game a kicker attempts a field goal. The ball remains in contact with the kicker's foot for 0.050 s, during which time it experiences an acceleration of 340m/s2. The ball is launched at an angle of 51∘ above the ground. Determine the horizontal and vertical components of the launch velocity.
Avxvy13m/s11m/sBvxvy21m/s11m/sCvxvy11m/s13m/sDvxvy17m/s21m/s
(a) A boy throws several balls out of the window of his house at different angles to the horizontal. All balls are thrown at speed u=10m/s and it was found that all of them hit the ground making an angle of 45° or larger than that with the horizontal. Find the height of the window above the ground [take g=10m/s2]
(b) A gun is mounted on an elevated platform AB. The distance of the gun at A from the edge B is AB=960m. Height of platform is OB=960m. The gun can fire shells with a velocity of u=100m/s at any angle. What is the minimum distance (OP) from the foot of the platform where the shell of gun can reach ?
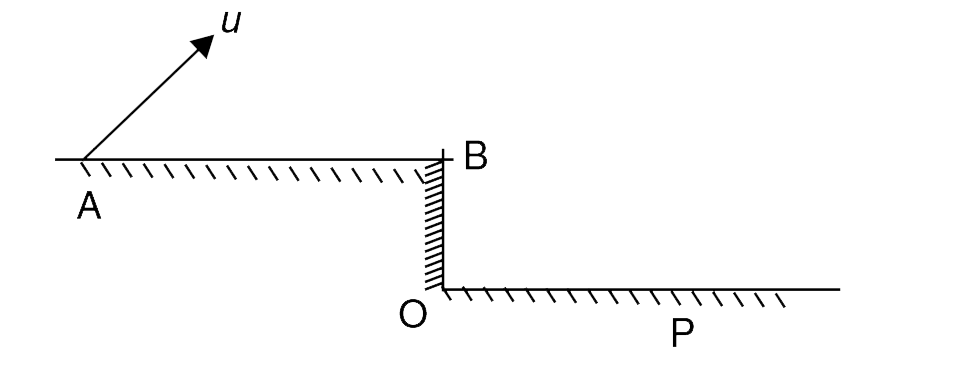
View SolutionThere is a tall cylindrical building standing in a field. Radius of the cylinder is R=8m. A boy standing at A (at a distance of 10 m from the centre of the cylindrical base of the building) knows that his friend is standing at B behind the building. The line joining A and B passes through the centre of the base of the building. Distance between A and B is 50 m. A wants to throw a ball to B but he realizes that the building is too tall and he cannot throw the ball over it. He throws the ball at a speed of 20m/s such that his friend at B has to move minimum distance to catch it.

(a) What is the minimum distance that boy at B will have to move to catch the ball?
(b) At what angle to the horizontal does the boy at A throws the ball? Assume that the ball is released and caught at same height above the ground.
[Take g=10m/s2 and sin−1(0.75)≅48.6∘
View SolutionA football kicker can give the ball an initial speed of 25 m/s. What are the (a) least and (b) greatest elevation angles at which he can kick the ball to score a field goal from a point 50 m in front of goalposts whose horizontal bar is 3.44 m above the ground?
View SolutionA football is kicked at a speed of 20m/s a projection angle of 45∘. A receiver on the goal line 25 metres away in the direction to the kink runs the same instant to meet the ball. Befrom it hits the ground?
View SolutionA football is kicked with speed 20ms−1 at a projection angle of 45∘ from the ground. A receiver on the goal line 20m away in the disrection of the kich runs the same instant to meet the ball. What must he his speed, of he is to catch the ball cefore it hits the ground ? Take g=10ms−2.
View SolutionThe drawings below (Fig. 5.37), show angles formed by the goalposts at different positions of a football player. The greater the angle, the better chance the player has of scoring a goal. For example, the player has a better chance of scoring a goal from Position A than from Position B.
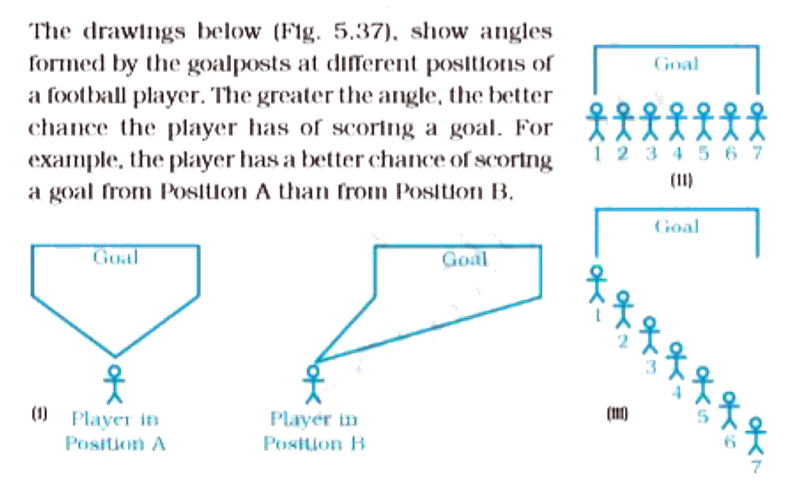
In Parts (a) and (b) given below it may help to trace the diagrams and draw and measure angles.
(a) Seven football players are practicing their kicks. They are lined up in a straight line in front of the goalpost [Fig.(ii)]. Which player has the best (the greatest) kicking angle?
(b) Now the players are lined up as shown in Fig. (iii). Which player has the best kicking angle?
(c) Estimate atleast two situations such that the angles formed by different positions of two players are complement to each other.
View Solution
