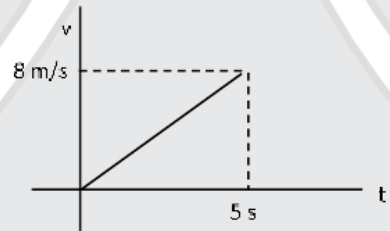
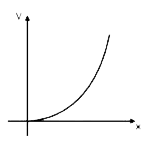
In a uniform electric field, a point charge of mass m and charge q is released from rest. If there are no other forces acting on the particle, then which of the following graphs, correctly show the dependence of the particles speed v on the distance x travelled by the particles speed v on the distance x travelled by it? [Graphs are schematic and not drawn to scale]
A
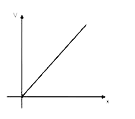
B
C
D
Video Solution
Text Solution
The correct Answer is:B
Using work - energy theorem. qEx=12mv2⇒υ2=2qEmx ⇒υ=√2qEm√x
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a uniform electric field, a point charge of mass m and charge q is released from rest. If there are no other forces acting on the particle, then which of the following graphs, correctly show the dependence of the particles speed v on the distance x travelled by the particles speed v on the distance x travelled by it? [Graphs are schematic and not drawn to scale]
ABCDA particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
A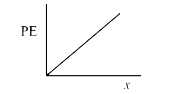
B
C
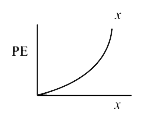D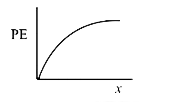
Figure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
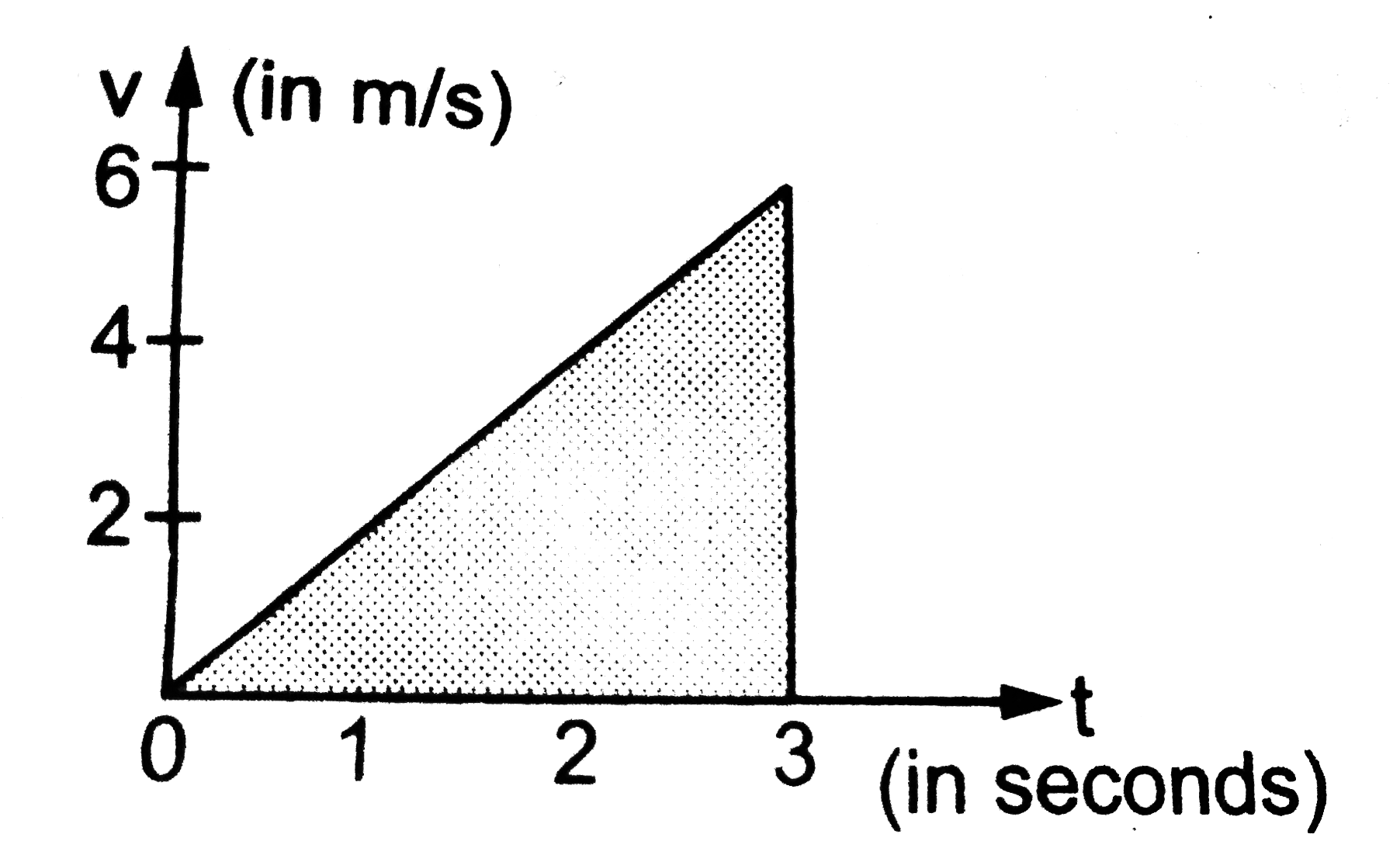A9mB5mC2mD1m
The v-t graph for a particle is as shown. The distance travelled in the first seconds is :
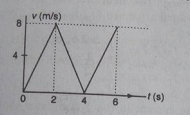
View SolutionThe v-t graph for a particle is as shown. The distance travelled in the first seconds is :
View SolutionA particle of mass and charge is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its kinetic energy on the distance travelled by it is correctly given by (graphs are schematic and not drawn to scale)
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionThe v−t graph for a particle is shown. The distance travelled in the first four seconds is:
View Solution