In a YDSE if a slab whose refractive index can be varied is palced in fron of one of the slits then the variation of resultant intensity of mid-point of screen with μ will be represented by (assume slits of equal width and there is no absorption by slab)
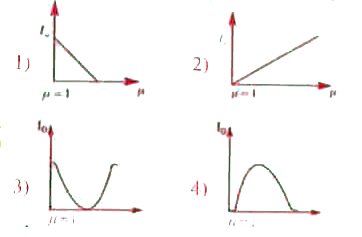
μ=1⇒△x=0 I= maximum
△x=(μ−1)t μ↑⏐⇒△x increases from 0 to λ2 to λ
Intensity first decreases then increases.
Topper's Solved these Questions
Similar Questions
In YDSE if a slab whose refractive index can be varied is placed in front of one of the slits. Then, the variation of resultant intensity at mid-point of screen with μ will be best represented by (mu is greater than or equal to 1)
View SolutionIn YDSE if a slab whose refractive index can be varied is placed in front of one of the slits. Then, the variation of resultant intensity at mid-point of screen with μ will be best represented by (mu is greater than or equal to 1)
View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionIn YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
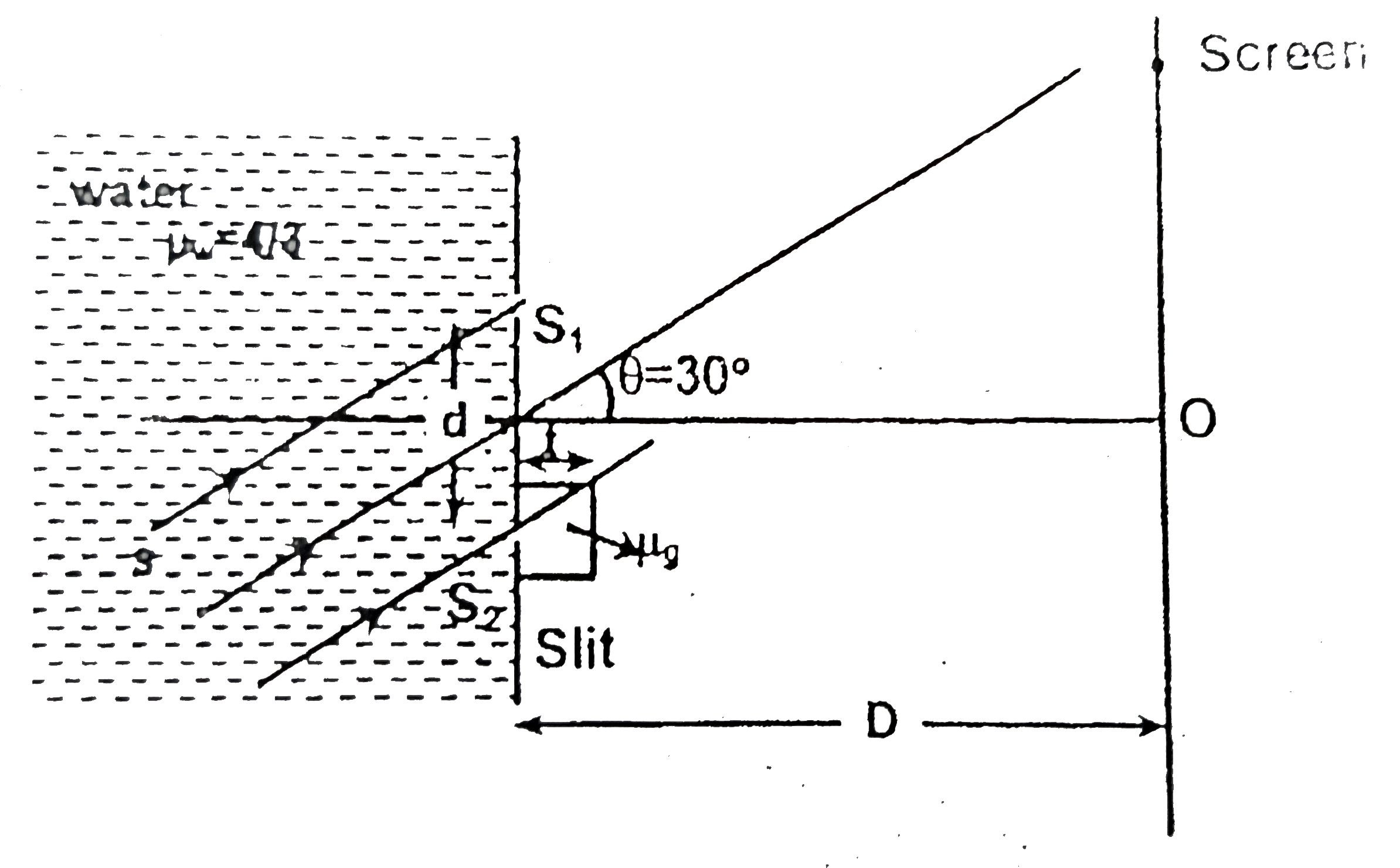
View SolutionIn a YDSE experiment the two slits are covered with a transparent membrane of negligible thickness which allows light to pass through it but does not allow water. A glass slab of thickness t=0.41mm and refractive index μg=1.5 is placed infront of one of the slits as shown in the figure. The separation between the slits is d=0.30mm. The entire space to the left of the slits is filled with water of refractive index μw=4/3.
A coherent light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1m from the slits, find
(a) the position of central maxima.
(b) the intensity at point O.
 View Solution
View SolutionIn young's double-slit experiment, both the slits produce equal intensities on a screen. A 100% transparent thin film of refractive index μ=1.5 is kept in front of one of the slits, due to which the intensity at the point O on the screen becomes 75% of its initial value. If the wavelength of monochromatic light is 720 nm, then what is the minimum thickness (in nm) of the film?
 View Solution
View SolutionMinimum thickness of a mica sheet having μ=32 which should be placed in front of one of the slits in YDSE is required to reduce the intensity at the centre of screen to half of maximum intensity is
View SolutionIn a doulble slit experiment when a thin film of thickness t having refractive index μ is introduced in from of one of the slits, the maximum at the centre of the fringe pattern shifts by one width. The value of t is (λ is the wavelength of the light used)
View SolutionIn Young's double slit experiment a mica plate of refractive index μ is introduced in the path of light coming from one of the slit . If the central bright fringe gets shifted to the point originally occupied by the fourth bright fringe, then the thickness of the mica plate will be (symbols have their usual meaning )
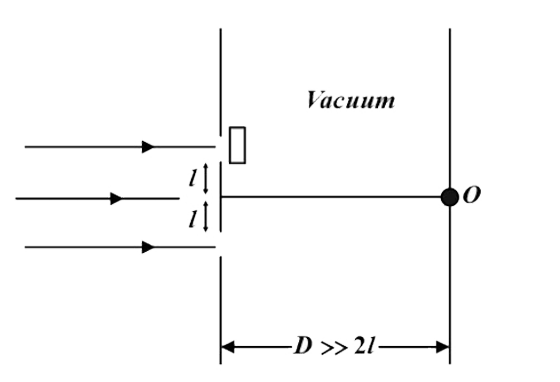
View SolutionA plate of thickness t made of a material of refractive index μ is placed in front of one of the slits in a double slit experiment. (a) Find the changes in he optical path due to introduction of the plate. (b) Wht should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero ? Wavelength of the light used is λ. Neglect any absorption of light in the plate.
View Solution

