In an inductor, current rises to a steady value at a constant rate. Comment.
To analyze the statement "In an inductor, current rises to a steady value at a constant rate," we can break it down step by step.
Step 1: Understanding the Inductor's Behavior
An inductor is a passive electrical component that stores energy in a magnetic field when electric current flows through it. The relationship between voltage (V), inductance (L), and the rate of change of current (Di/dt) is given by the formula:
V=LdIdt
Step 2: Analyzing the Formula
From the formula, we can rearrange it to express the rate of change of current:
dIdt=VL
This indicates that the rate of change of current (dI/dt) is proportional to the voltage across the inductor and inversely proportional to its inductance.
Step 3: Integrating the Equation
To find the current (I) over time, we need to integrate the equation:
∫dI=∫VLdt
Assuming V is constant, we can simplify this to:
I=VLt+I0
where I0 is the initial current at time t=0.
Step 4: Exponential Growth of Current
However, if we consider a situation where the voltage is applied suddenly (like in an RL circuit), the current does not rise linearly. Instead, it follows an exponential growth pattern:
I(t)=Imax(1−e−RLt)
where Imax is the maximum steady-state current, R is the resistance, and e is the base of the natural logarithm.
Step 5: Conclusion
Thus, the statement that "current rises to a steady value at a constant rate" is incorrect. Instead, the current in an inductor rises to a steady value at an exponential rate. The current increases rapidly at first and then gradually approaches the steady-state value.
Final Comment
In conclusion, the correct interpretation is that in an inductor, the current rises to a steady value at an exponential rate, not at a constant rate.
---
An inductor is a passive electrical component that stores energy in a magnetic field when electric current flows through it. The relationship between voltage (V), inductance (L), and the rate of change of current (Di/dt) is given by the formula:
V=LdIdt
From the formula, we can rearrange it to express the rate of change of current:
dIdt=VL
This indicates that the rate of change of current (dI/dt) is proportional to the voltage across the inductor and inversely proportional to its inductance.
To find the current (I) over time, we need to integrate the equation:
∫dI=∫VLdt
Assuming V is constant, we can simplify this to:
I=VLt+I0
where I0 is the initial current at time t=0.
However, if we consider a situation where the voltage is applied suddenly (like in an RL circuit), the current does not rise linearly. Instead, it follows an exponential growth pattern:
I(t)=Imax(1−e−RLt)
where Imax is the maximum steady-state current, R is the resistance, and e is the base of the natural logarithm.
Thus, the statement that "current rises to a steady value at a constant rate" is incorrect. Instead, the current in an inductor rises to a steady value at an exponential rate. The current increases rapidly at first and then gradually approaches the steady-state value.
In conclusion, the correct interpretation is that in an inductor, the current rises to a steady value at an exponential rate, not at a constant rate.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Problems (Level - I)16videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Problem (Level - II)9videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Exercies (Short Answer Questions)4videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
Similar Questions
Assertion: Current versus time graph is as shown in figure, rms value of current is 4A.
Reason: For a constant current, rms current is equal to that constant values.
Reason: For a constant current, rms current is equal to that constant value.
 View Solution
View SolutionWhen the current through a solenoid increases at a constant rate, the induced current in the solenoid
View Solution
Knowledge Check
- Question 1 - Select One
An electric heater is connected to the voltage supply. After few seconds Current gets its steady value then its initial current will be
Aequal to its steady currentBslightly higher than its steady currentCslightly less than its steady currentDzero
Assertion If current shown in the figure is increasing, then
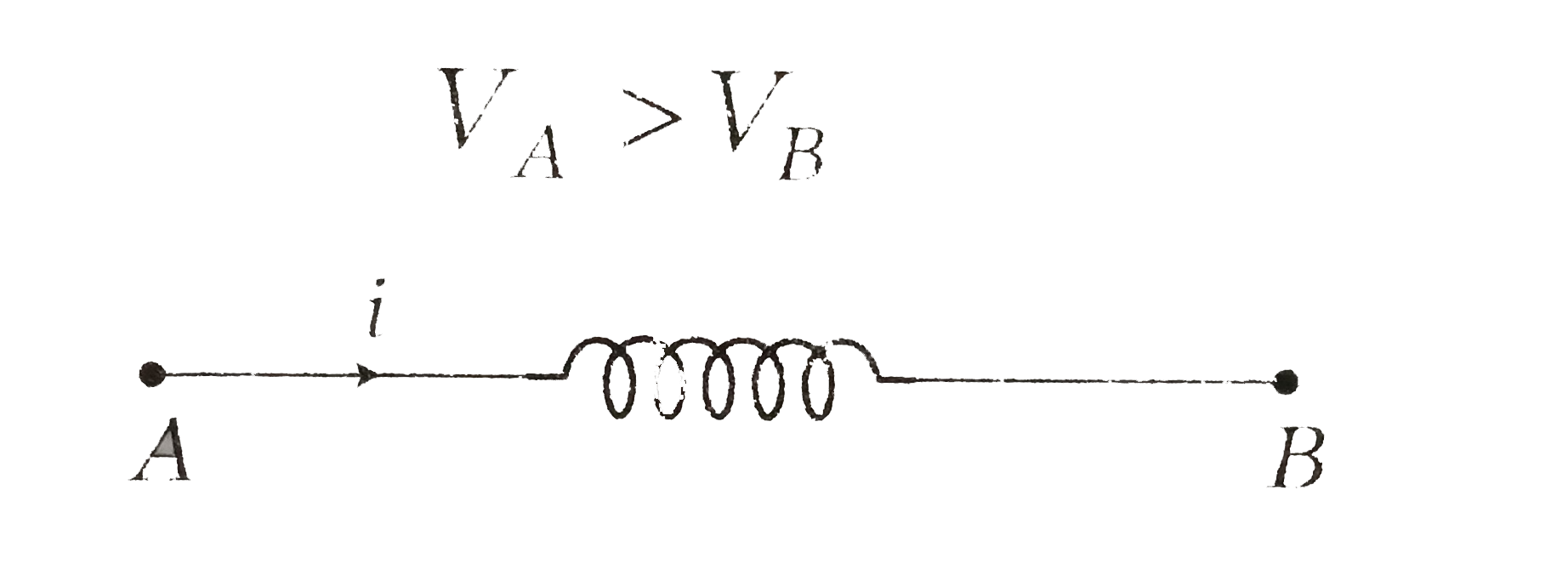
Reason IF current passing through an inductor is constant, then both ends of the inductor are at same potential.View SolutionRate constant value depends on:
View SolutionAn inductor coil carries a steady state current of 2.0 A when connected across an ideal battery of emf 4.0 V. if its inductance is 1.0 H, find the time constant of the circuit.
View SolutionAn e.m.f. of 5volt is produced by a self-inductance, when the current changes at a steady rate from 3A to 2A 1millisecond. The value of self-inductance is
View SolutionA dry cell of emf 1.5V and internal resistance 0.10Ω is connected across a resistor in series with a very low resistance ammeter. When the circuit is switched on , the ammeter reading settles to a steady value of 2.0A.
(i) What is the steady rate of chemical energy consumption of the cell ?
(ii) What is the steady rate of energy dissipation inside the cell ?
(ii) What is the steady rate of energy dissipation inside the resistor ?
(iv) What is the steady power out put of the source?View SolutionIn the following circuit the switch is closed at t=0.Intially there is no current in inductor.Find out current the inductor coil as a function of time.
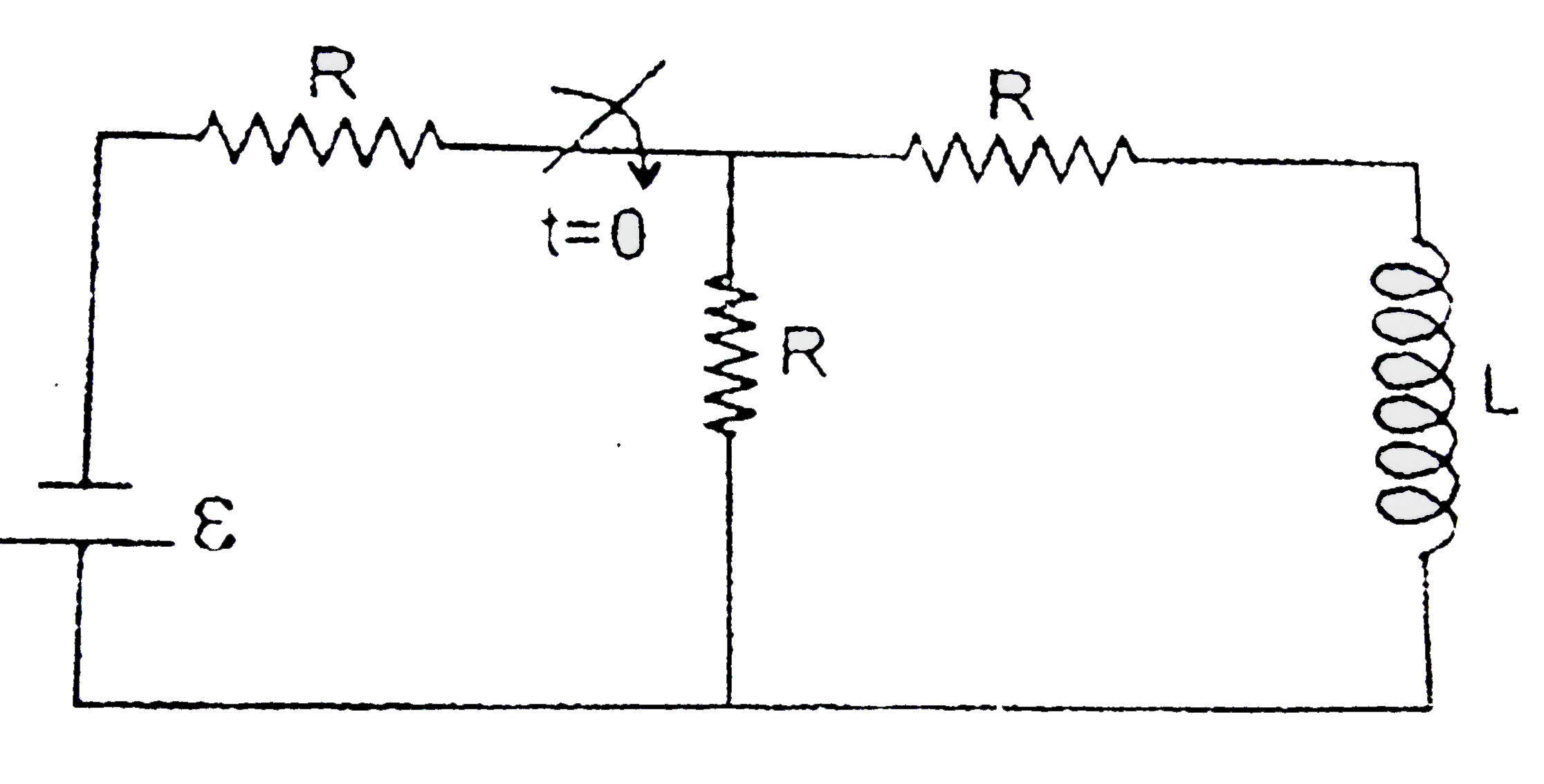 View Solution
View SolutionA resistor and inductor are connected in series through a battery.
The switch is closed at time t=0 . Then what is the magnitude of current flowing when rate of increases of magnetic energy in the inductor is maximumView Solution
