A dry cell of emf 1.5V and internal resistance 0.10Ω is connected across a resistor in series with a very low resistance ammeter. When the circuit is switched on , the ammeter reading settles to a steady value of 2.0A.
(i) What is the steady rate of chemical energy consumption of the cell ?
(ii) What is the steady rate of energy dissipation inside the cell ?
(ii) What is the steady rate of energy dissipation inside the resistor ?
(iv) What is the steady power out put of the source?
To solve the problem step by step, we will address each part of the question sequentially.
Given Data:
- EMF of the dry cell, E=1.5V
- Internal resistance of the dry cell, r=0.1Ω
- Steady current, I=2.0A
(i) Steady Rate of Chemical Energy Consumption of the Cell
The steady rate of chemical energy consumption of the cell can be calculated using the formula:
Pchemical=E×I
Substituting the values:
Pchemical=1.5V×2.0A=3.0W
(ii) Steady Rate of Energy Dissipation Inside the Cell
The energy dissipation inside the cell can be calculated using the formula:
Pinternal=I2×r
Substituting the values:
Pinternal=(2.0A)2×0.1Ω=4.0×0.1=0.4W
(iii) Steady Rate of Energy Dissipation Inside the Resistor
To find the energy dissipation inside the resistor, we can use the difference between the total power output of the cell and the power dissipated inside the cell:
Presistor=Pchemical−Pinternal
Substituting the values:
Presistor=3.0W−0.4W=2.6W
(iv) Steady Power Output of the Source
The steady power output of the source is equal to the power dissipated in the resistor:
Poutput=Presistor=2.6W
Summary of Results:
1. Steady rate of chemical energy consumption of the cell: 3.0 W
2. Steady rate of energy dissipation inside the cell: 0.4 W
3. Steady rate of energy dissipation inside the resistor: 2.6 W
4. Steady power output of the source: 2.6 W
- EMF of the dry cell, E=1.5V
- Internal resistance of the dry cell, r=0.1Ω
- Steady current, I=2.0A
The steady rate of chemical energy consumption of the cell can be calculated using the formula:
Pchemical=E×I
Substituting the values:
Pchemical=1.5V×2.0A=3.0W
The energy dissipation inside the cell can be calculated using the formula:
Pinternal=I2×r
Substituting the values:
Pinternal=(2.0A)2×0.1Ω=4.0×0.1=0.4W
To find the energy dissipation inside the resistor, we can use the difference between the total power output of the cell and the power dissipated inside the cell:
Presistor=Pchemical−Pinternal
Substituting the values:
Presistor=3.0W−0.4W=2.6W
The steady power output of the source is equal to the power dissipated in the resistor:
Poutput=Presistor=2.6W
1. Steady rate of chemical energy consumption of the cell: 3.0 W
2. Steady rate of energy dissipation inside the cell: 0.4 W
3. Steady rate of energy dissipation inside the resistor: 2.6 W
4. Steady power output of the source: 2.6 W
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Solved Examples
13 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.1
22 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
A cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
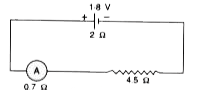
What would be the reading of the ammeter ?
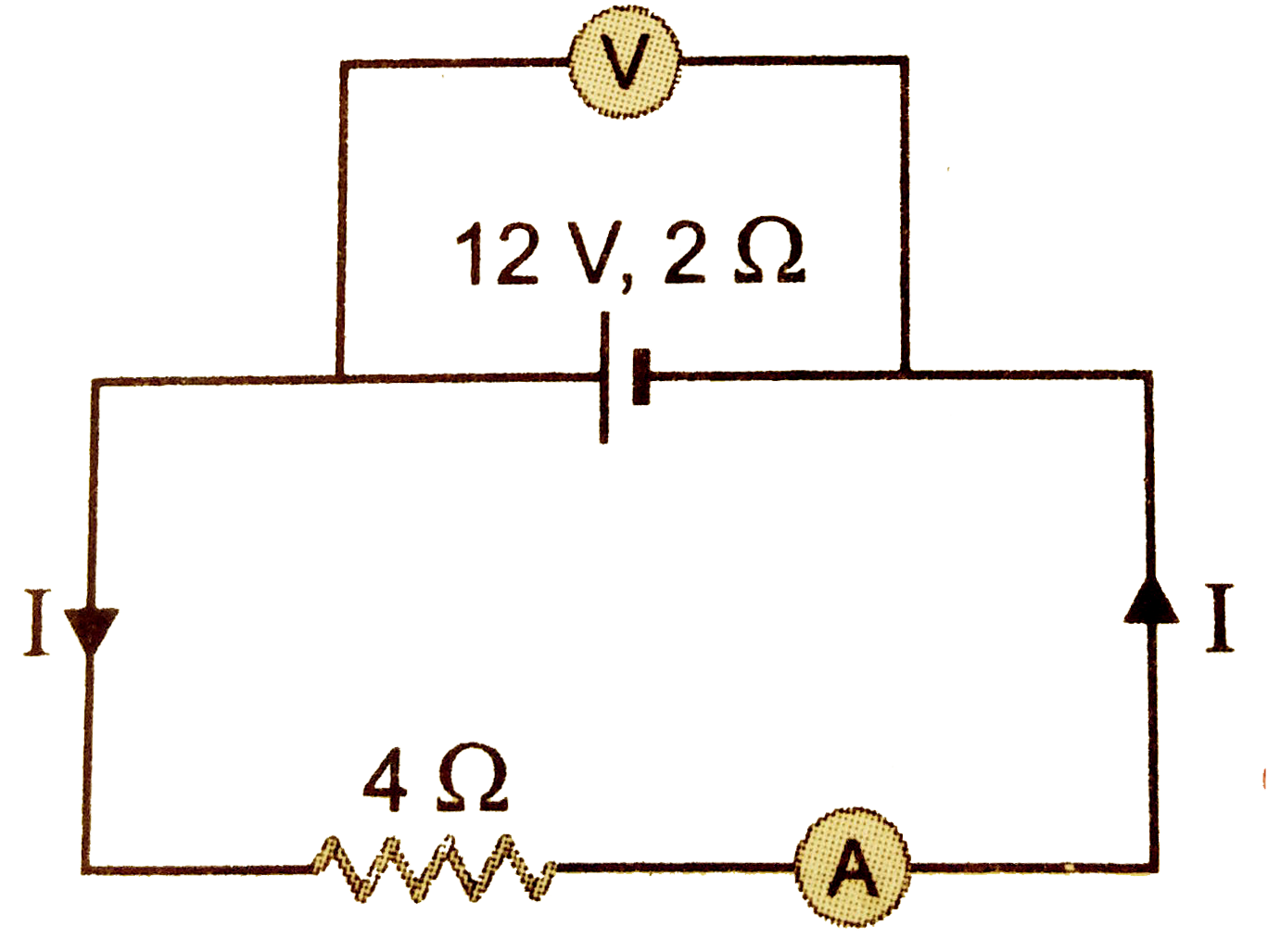
View SolutionA battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
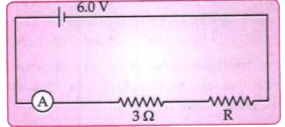
Calculate the value of the unknown resistor R.
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the p.d. across each resistor
View SolutionEight cells marked 1 to 8, each of emf 5V and internal resistance 0.2Ω are connected as shown. What is the reading of ideal voltmeter ?
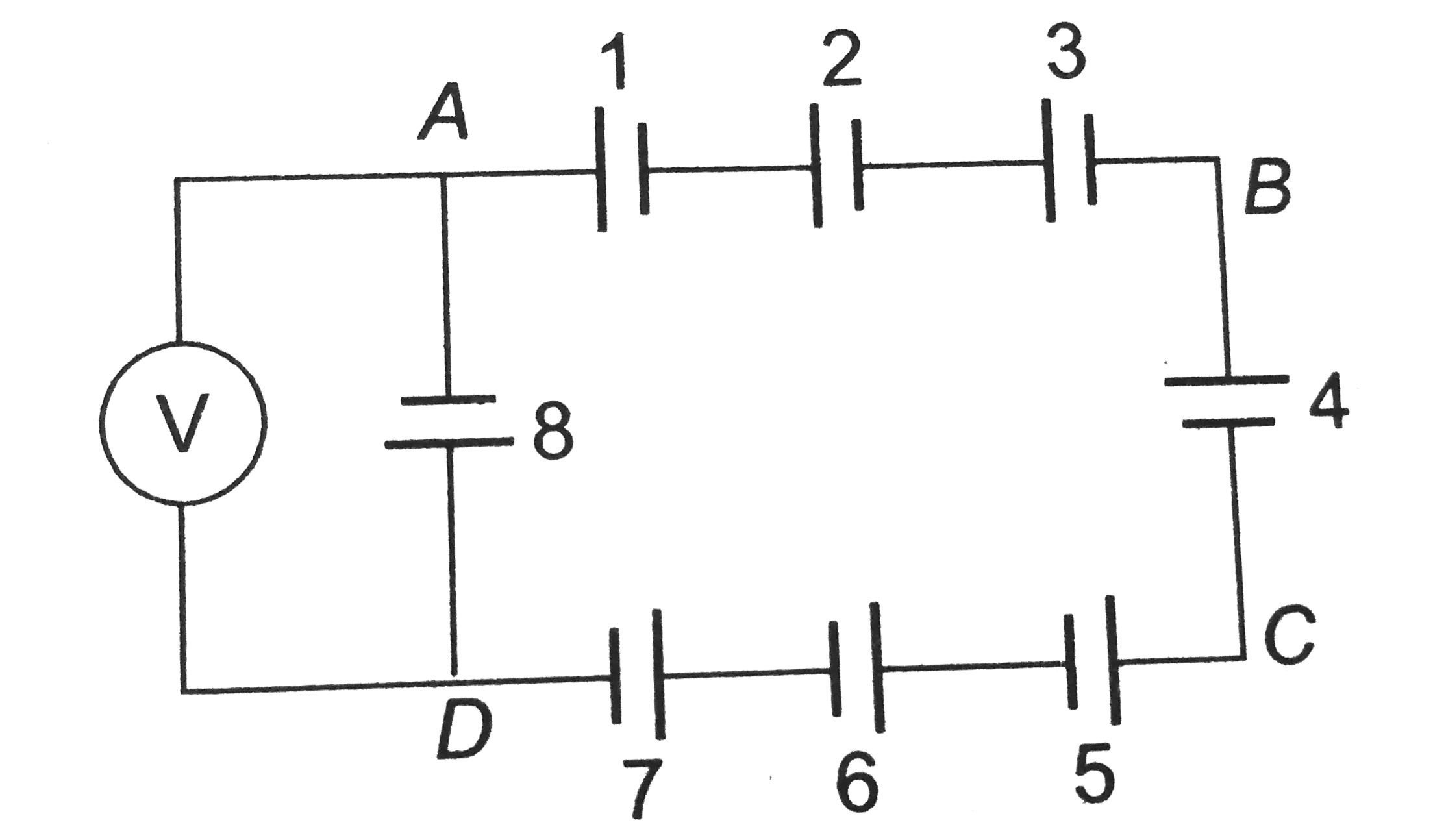
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the current in the circuit,
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig. What is the potential difference across the terminals of the cell ?
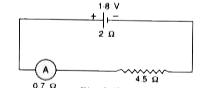
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
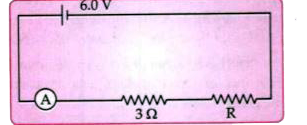
Calculate the power dissipated in the 3Ω resistor.
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the voltage drop when the current is flowing.
View Solution
