In an oscillating circuit shown in figure, the coil inductance is equal to L=2.5μF. The capacitor have capacitances C1=2.0μF and C2=3.0μF. The capacitors were charged to a voltage V=180V, and then the switch Swwas closed. Find :
(a) the natural oscillation frequency,
(b) the peak value of the current flowing through the coil.
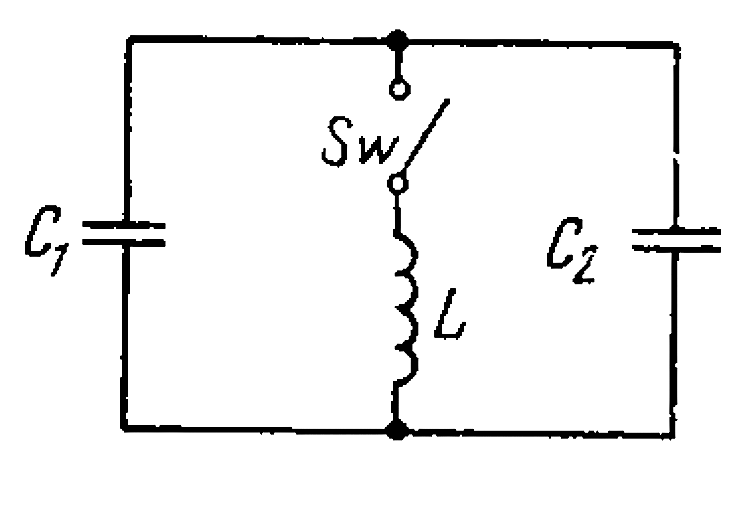
The equations of the L−C circuit are
Lddt(I1+I)=C1V−∫I1dtC1=C2V−∫I2dtC2
Differentiating again
L(I1+I2)=−1C2I1=−1C2I2
Then I1=C1C1−C2I,I2=C2C1+C2I,
I=I1+I2
so L(C1+C2)I+I=0
or I=I0sin(ω0t+α)
where ω20=1L(C1+C2)( Part a)
( Hence T=2πω0=0.7ms)
At t=0,I=0 so α=0
I=I0sinω0t
The peak value of the current if I0 and it is related to the voltage V by the first equation
LI=V−∫Idt/(C1+C2)
or +Lω0I0cosω0t=V−1C1+C2∫t0I0sinω0tdt
( The P.D. across the inductance is V at t=0)
=V+1C1+C2.I0ω0(cosω0t−1)
Hence I0=(C1+C2)ω0V=V√C1+C2L=8.05A.

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Knowledge Check
In the circuit shown in the figure, the total charge is 750μC and the voltage across capacitor C2 is 20 V. Then the charge on capacitor C2 is:
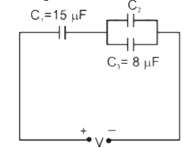 A650μCB450μCC590μCD160μC
A650μCB450μCC590μCD160μC
A capacitor of capacitance C=2.0±0.1μF is charged to a voltage V=20±0.2V. What will be the charge Q on the capacitor ? Use Q=CV.
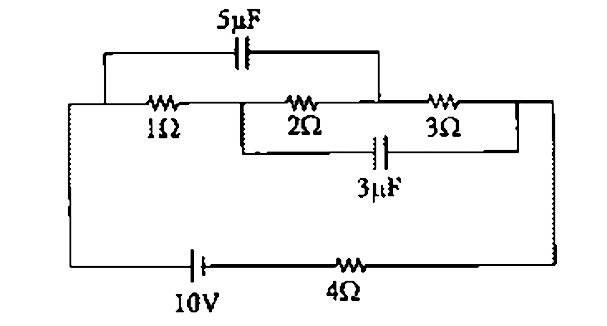
View SolutionIn the circuit shown in figure-3.395, find the charges on capacitors of capacitances 5μFand3μF, in steady state.
View SolutionAn oscillating circuit consists of a capacitor with capacitance C, a coil of inductance L with negligible resistance, and aswitch. With the switch disconnected , the capacitor was charged to a voltage Vm and then at the moment t=0 the switch was closed . Find :
(a) the current (I(t)) in the circuit as a function of time,
(b) the emf of self- inductance in the coil at the moments when the electric energy of the capacitor is equal to that of the current in the coil.
View SolutionFour capacitors of capacitance 10μF and a battery of 2V are arranged as shown. How much μC charge will flow through AB after the switch S is closed ?
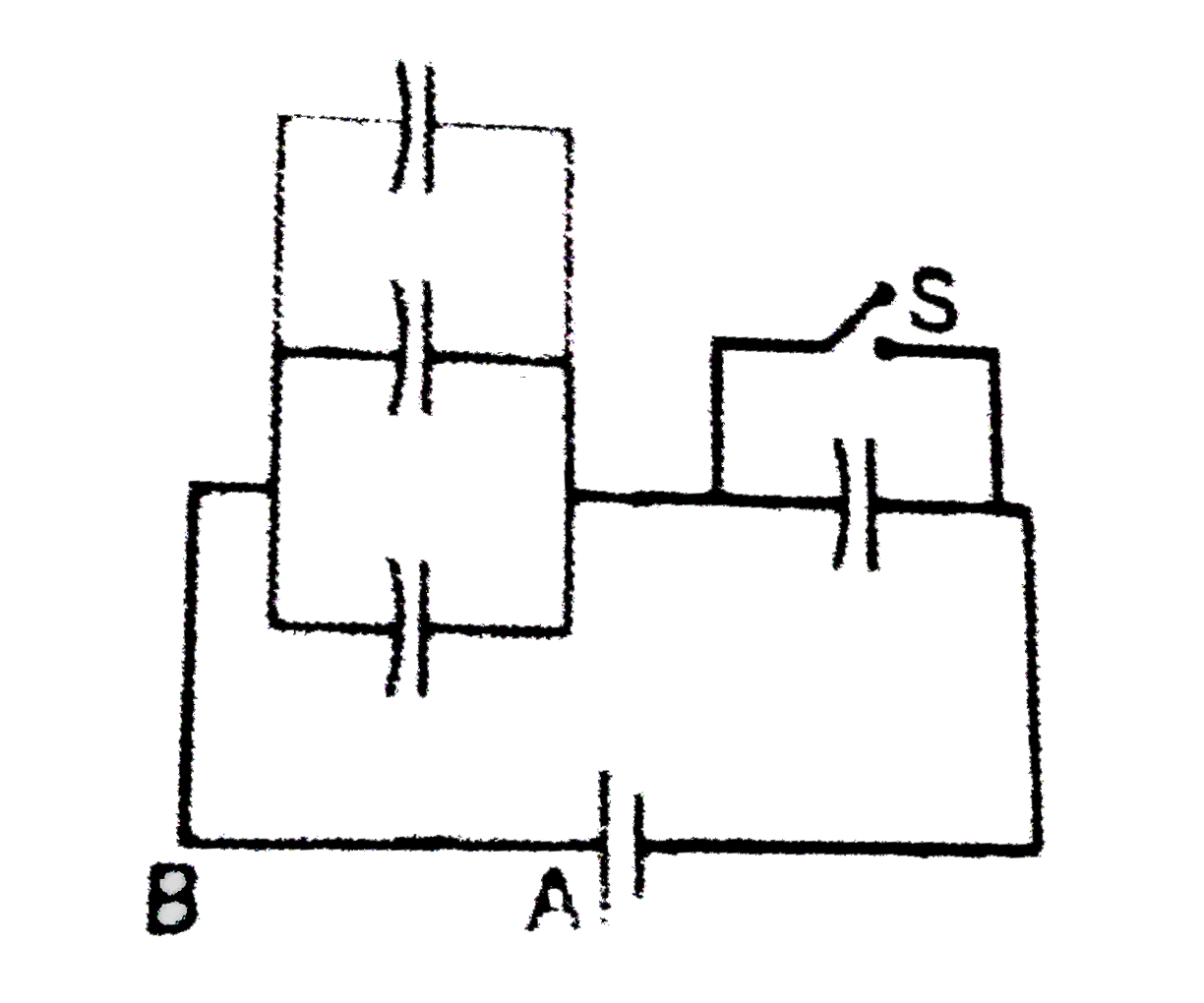
View SolutionFour capacitors of capacitance 10μF and a battery of 2V are arranged as shown. How much μC charge will flow through AB after the switch S is closed ?
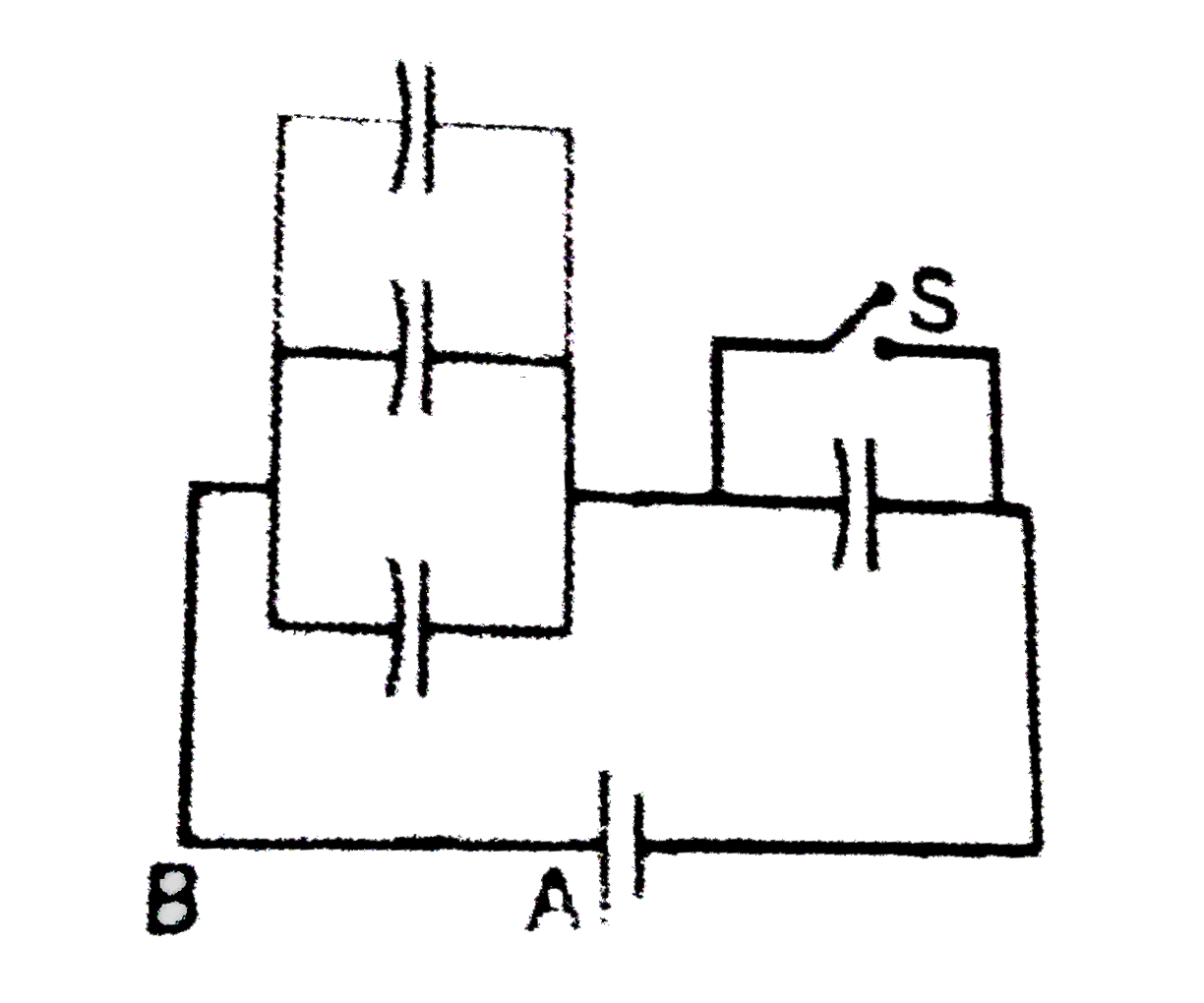
View SolutionIn the circuit shown in figure C1=1μF and C2=2μF. The capacitor C1 is charged to 100V and the capacitor C2 is charged to 20V. After charging then are connected as shown. When the switches S1,S2 and S3 are closed, the charged flowing through S1 is
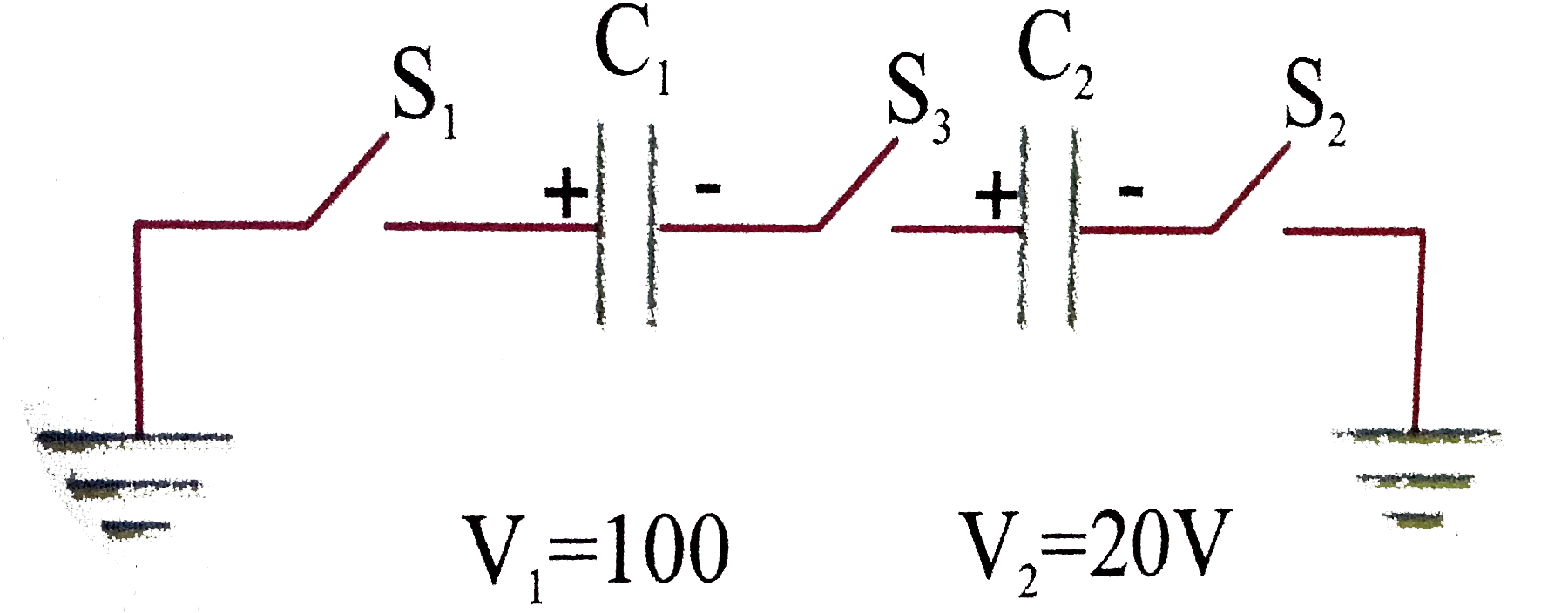 .
.
View SolutionIn the circuit shown in the figure, the total charge is 750μC and the voltage across capacitor C2 is 20 V. Then the charge on capacitor C2 is:

View Solution

