In co-axial concentric coils of radius r1 and r2 such that r1<<r2 Fig. find direction of induced current when K is (i) pressed (ii) released.
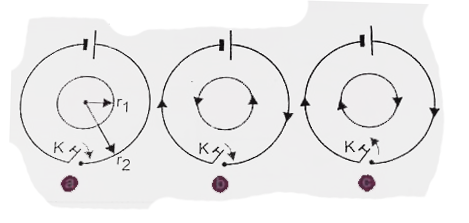
(i) When key K is pressed, current in outer coil increases from 0 to maximum. Current induced in inner coil opposes the growth of current in outer coil, by flowing in the opposite direction, i.e. in anticlock wise direciton, as shown in Fig. (ii) When key K is released, current in outer coil decreases from maximum to zero. Current induced in inner coil opposes the decay of current in outer coil, by flowing in the same direction, i.e. in clockwise direction as shown in Fig.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
A thin spherical conducting shell of radius r1 carries a charge Q. Concentric with it is another thin metallic spherical shell of radius r2(r2>r1). Calculate electric field at distance r when (i) r<r1 ,(ii) r1<r<r2 and (iii) r>r2.
What will be the field in above cases if outer shell (a) is given charge q and (b) is earthed ?View SolutionIn ΔABC, if r1<r2<r3, then find the order of lengths of the sides
View Solution
Knowledge Check
- Question 1 - Select One
Space between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
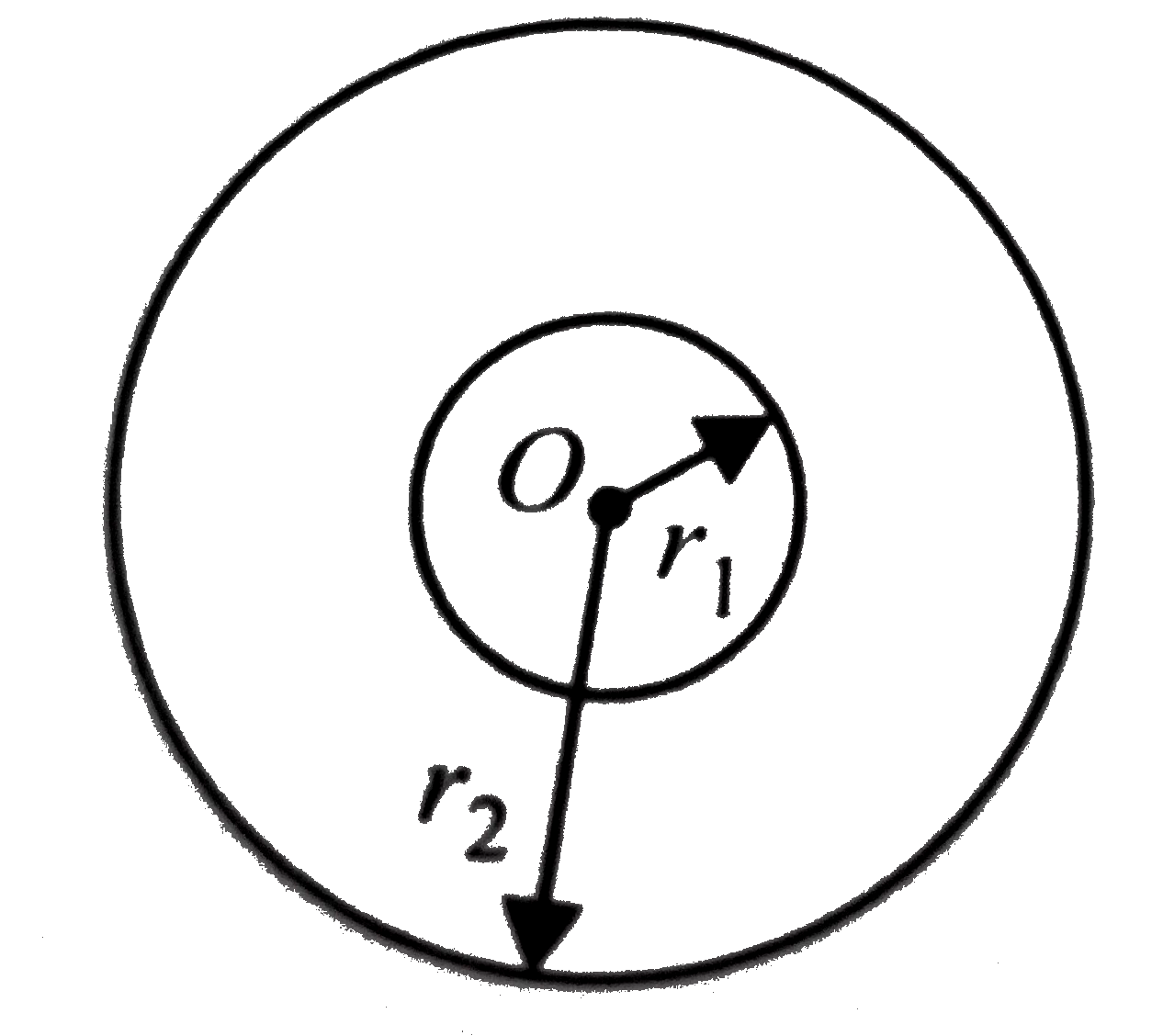 Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these. - Question 2 - Select One
The capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1 - Question 3 - Select One
Two plane circular coilds P and Q have radii r1 and r2, respectively, (r1<<r2) and are coaxial as shown in fig. The number of turns in P and Q are respectively N1 and N2. If current in coil Q is varied steadily at a rate x ampere/second then the induced emf in the coil P will be approximatery -
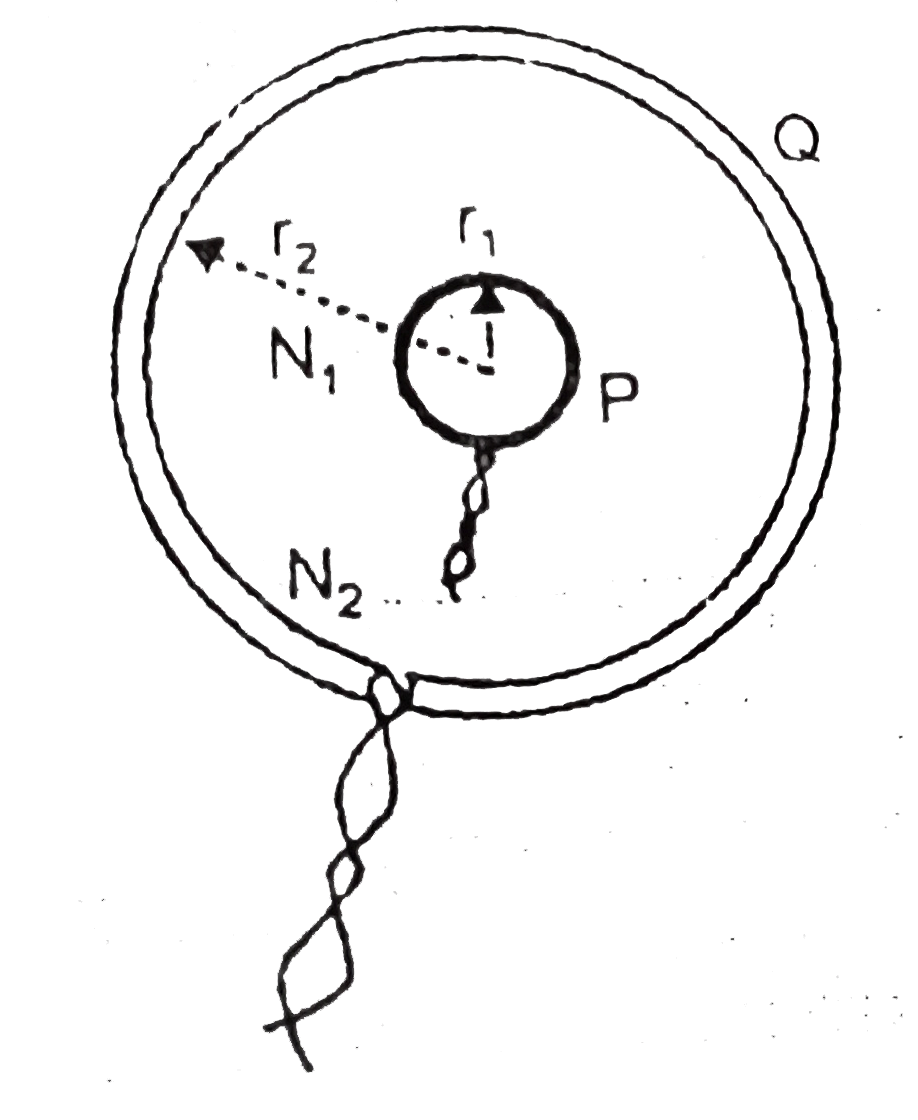 Aμ0N1N2πr21Bμ0N1N2πr21xCμ0N1N2πr21x/2r2Dzero
Aμ0N1N2πr21Bμ0N1N2πr21xCμ0N1N2πr21x/2r2Dzero
(a) Explain the meaning of the term mutual inductance. Consider two concentric circular coils, one radius r1 and the other of radius r2(r1<r2) placed coaxially with centres coinciding with each other. Obtain the expression for the mutual inductance of the arrangement.
(b) A rectangular coil of area A, having number of turns N is rotated at 'f' revoluation per second in a uniform magnetic field B, the field being perpendicular to the coil. Prove that maximum emf induced in the coil is 2πfNBA.View SolutionThe figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is
 View Solution
View SolutionProve that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionA and V are semi - spherical surfaces of radius r1andr2(r1<r2)withE1andE2 as the electric fields a the their surfaces. Charge q0 is placed as shown. What is the condition which may be satisfied ?
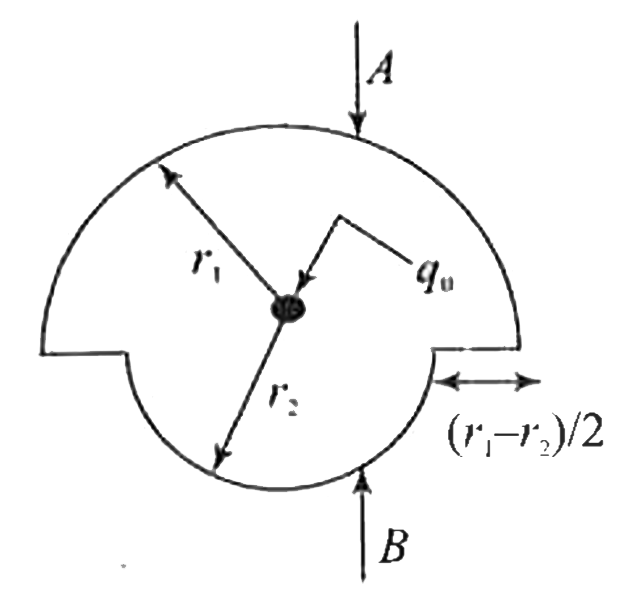 View Solution
View Solution

