Find out the position of particle as a function of time which is moving in a straight line with an acceleration a=5x, where x is position.
(i) At t=0 the particle is at x=0 (ii) Mass of the object is 5kg
Question can be solved by information I only.
Question can be solved by information II only
Question can be solved by information I and II in combined form only.
Question can not be solved by both the informations only.
The correct Answer is:D
To find the position of a particle as a function of time when it is moving in a straight line with an acceleration given by a=5x, we can follow these steps:
Step 1: Understand the relationship between acceleration, velocity, and position
The acceleration a can be expressed in terms of velocity v and position x as:
a=dvdt
Using the chain rule, we can rewrite this as:
a=vdvdx
Step 2: Set up the equation
Given that a=5x, we can substitute this into our equation:
vdvdx=5x
Step 3: Separate variables and integrate
We can separate the variables:
vdv=5xdx
Now, we integrate both sides:
∫vdv=∫5xdx
This gives us:
v22=5x22+C
where C is the integration constant.
Step 4: Solve for velocity
Multiplying through by 2, we have:
v2=5x2+2C
Taking the square root of both sides, we find:
v=√5x2+2C
Step 5: Relate velocity to time
Recall that velocity v is also defined as:
v=dxdt
Thus, we can write:
dxdt=√5x2+2C
Step 6: Separate variables again
We can separate the variables again:
dx√5x2+2C=dt
Step 7: Integrate to find position as a function of time
Now we need to integrate both sides. This integral can be complex, but we can denote it as:
∫dx√5x2+2C=∫dt
Let C2 be the constant of integration for the time side.
Step 8: Apply initial conditions
At t=0, x=0. We can use this to find the constant C and C2. However, we have two constants and only one initial condition, which means we cannot uniquely determine the function without additional information.
Conclusion
Thus, the position of the particle as a function of time cannot be uniquely determined with the given information.
---
The acceleration a can be expressed in terms of velocity v and position x as:
a=dvdt
Using the chain rule, we can rewrite this as:
a=vdvdx
Given that a=5x, we can substitute this into our equation:
vdvdx=5x
We can separate the variables:
vdv=5xdx
Now, we integrate both sides:
∫vdv=∫5xdx
This gives us:
v22=5x22+C
where C is the integration constant.
Multiplying through by 2, we have:
v2=5x2+2C
Taking the square root of both sides, we find:
v=√5x2+2C
Recall that velocity v is also defined as:
v=dxdt
Thus, we can write:
dxdt=√5x2+2C
We can separate the variables again:
dx√5x2+2C=dt
Now we need to integrate both sides. This integral can be complex, but we can denote it as:
∫dx√5x2+2C=∫dt
Let C2 be the constant of integration for the time side.
At t=0, x=0. We can use this to find the constant C and C2. However, we have two constants and only one initial condition, which means we cannot uniquely determine the function without additional information.
Thus, the position of the particle as a function of time cannot be uniquely determined with the given information.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-04 [A]
28 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-4[B]
14 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 4
6 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionFigure shows the position of a particle moving on the X-axis as a function of time.

View SolutionFigure shows the position of a particle moving on the x - axis as a function of time
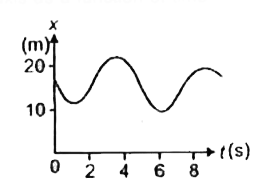
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
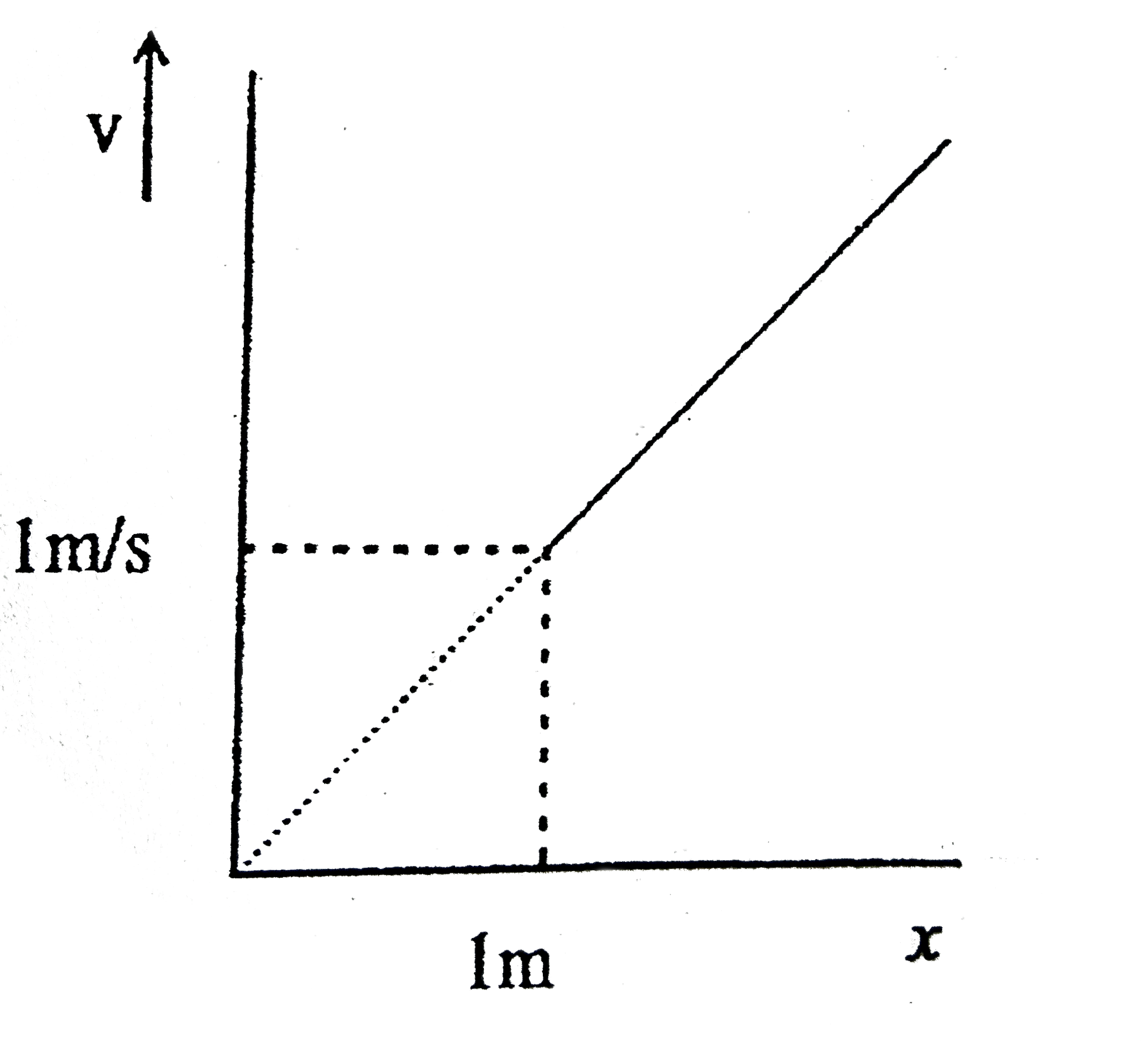
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View SolutionThe position of a particle moving on a straight line is proportional to the cube of the time elapsed. How does the acceleration of the particle depend on time elapsed?
View SolutionA particle starts to move in a straight line from a point with velocity 10 m s−1 and acceleration - 2.0 ms−2. Find the position and velocity of the particle at (i) t = 5 s, (ii) t' = 10 s.
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The acceleration of the particle is
View SolutionThe position of a particle moving on a stringht line under rthe action of a force is given as x=50t−5t2 Here, x is in metre and t is in second. If mass of the particle is 2 kg, the work done by the force acting on the particle in first 5 s is.
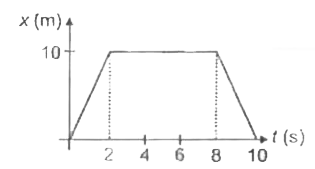
View SolutionThe position - time graph for a particle moving along a straight line is shown in figure. The total distance travelled by it in time t = 0 to t = 10 s is
View Solution