In Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the period of oscillation T?
The stick is not a simple pendulum because its mass is not concentrated in a bob at the end opposie the pivot point- so the stick is a physical pendulum.
Calculations: The period for a physical pendulum is given by Eq 15.45, for which we need the rotational inertia I of the stick about the pivot point. We can treat the stick as a uniform rod of length L and mass m. Then I=1/3mL2, and the distance h in Eq. 15.45 is 1/2L. Substituting these quantities into Eq. 15.45, we find
T=2π√Imgh=2π
⎷13mL2mg(12L)
=2π√2L3g
=2π√(2)(1.00m)(3)(9.8m/s2)=1.64s
Note: the result is independent of the pendulum.s mass m.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint8videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems39videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)4videos
PHOTONS AND MATTER WAVES
Similar Questions
In Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the distance L0 between the pivot point O of the stick and the center of oscillation of the stick?View SolutionA uniform stick of length l is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance d from the centre of mass. The time period of small oscillation has a minimum value when d/l is
View Solution
Knowledge Check
- Question 1 - Select One
A uniform stick of length l is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance d from the centre of mass. The time period of small oscillation has a minimum value when d/l is
A1√2B1√12C1√3D1√6 - Question 2 - Select One
A metre stick swinging about its one end oscillates with frequency f0. If the bottom half of the stick was cut off, then its new oscillation frequency will be :
Af0B√2f0C2f0D2√2f0 - Question 3 - Select One
A metre stick swinging about its one end oscillates with frequency f0. If the bottom half of the stick was cut off, then its new oscillation frequency will be :
Af0B√2f0C2f0D2√2f0
In Fig. 15.33, a stick of length L= 1.65 m oscillates as a physical pendulum. (a) What value of distance x between the stick's center of mass and its pivot point O gives the least period? (b) What is that least period?
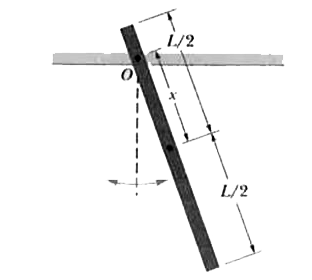 View Solution
View SolutionA mass suspended from a spring of spring constant k is made to oscillate with a time period T. Now, the spring is cut into three equal parts and the mass is suspended from one of the parts. What will be the new time period of oscillations?
View SolutionA metre stick swinging about its one end oscillates with frequency f0. If the bottom half of the stick was cut off, then its new oscillation frequency will be :
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA meter stick in form of a uniform rod is hinged at a distance x from the centre. It undergoes SHM with a time period of 2π3√75 sec. What is the value of x.
View Solution

