In Fig if f1,f2 and T are the friction forces on 2kg block 3kg block and tension in the string respectively the find their value initially before applying the forces tension in string was zero


fl1=μ1m1g=0.1×2×10=2N
fl2=μ2m2g=0.2×3×10=6N
T+fl2=8⇒T=2N
f1+1=T⇒f1=T−1=2−1=1N
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.3
27 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Knowledge Check
Force of friction and tension in a string are
AGravitational forcesBElectromagnetic forcesCNuclear forcesDWeal forcesIn the question number 91, if a force Fis applied to 20 kg block, then the tension in the string is
A100NB200NC300ND400N

Find out the acceleration of the blocks and tensions in the strings.
View SolutionIn the above example, if two blocks have masses 1kg and 2kg respectively then find their acceleration and tension in different string.
View SolutionThe block of mass m is at rest. Find the tension in the string A .

View SolutionIn the arragement of figure assume negligible friction between the blocks and table. If F the pulling force and m1 and m2 the masses are known, then the tension in the string is :
View Solution1.Consider the situation shown in figure (6-E2).Calculate (a) the acceleration of the 1⋅0kg blocks,(b) the tension in the string connecting the 1.0kg blocks and (c) the tension in the string attached to 0.50kg.
View SolutionTwo block of masses m1andm2 are lying on a frictionless horizontal table connected by a light string m2 is pulled by horizontal force F. Calculate the tension in the string .
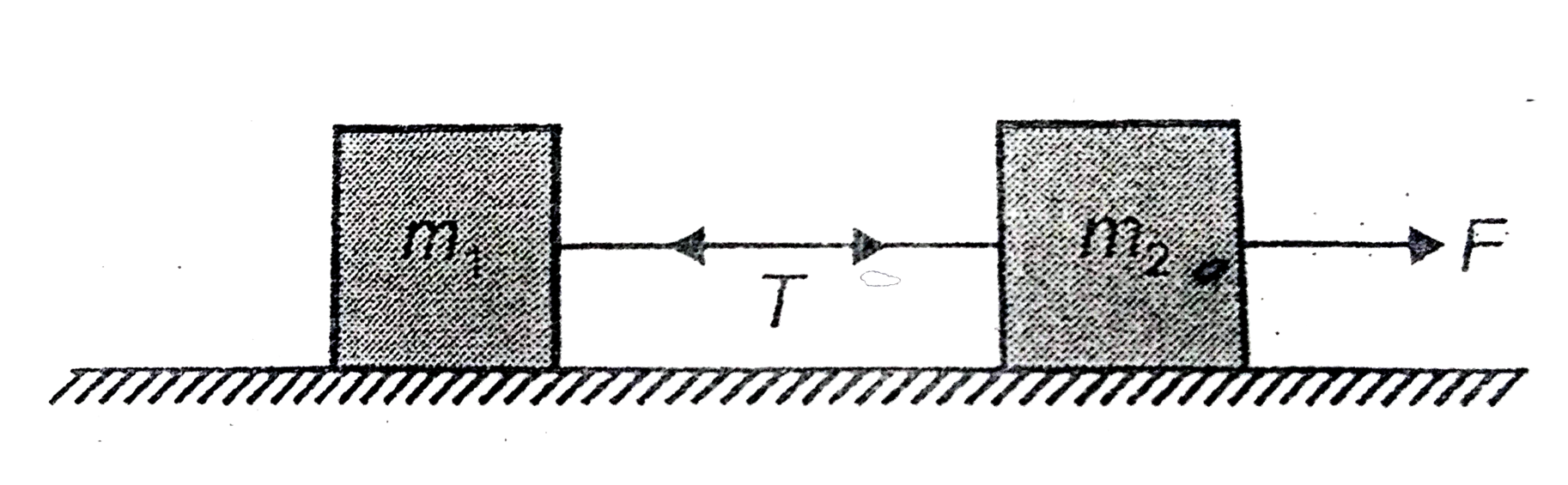
View Solution


