In Figure, a light ray is incident at angle on a series of five transparent layers with parallel boundaries. For layers 1 and 3. , and . (a) At what angle does the light emerge back into air at the riglit? (b) How much time does the light take to travel through layer 3?

(a) (same as incident angle), (b) s
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
66 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
23 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT
6 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
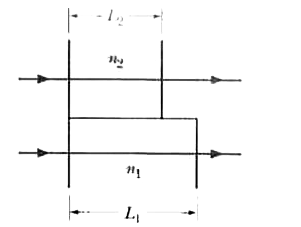
Two waves of light in air, of wavelength λ=600.0nm, are initially in phase. They then both travel through a layer of plastic as shown in Figure, with L1=4.00μm,L2=3.50μm,n1=1.42, and n2=1.60. (a) What multiple of λ gives their phase difference after they both have emerged from the layers? (b) If the waves later arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, interme- diate but closer to fully constructive, or intermediate but closer to fully destructive?
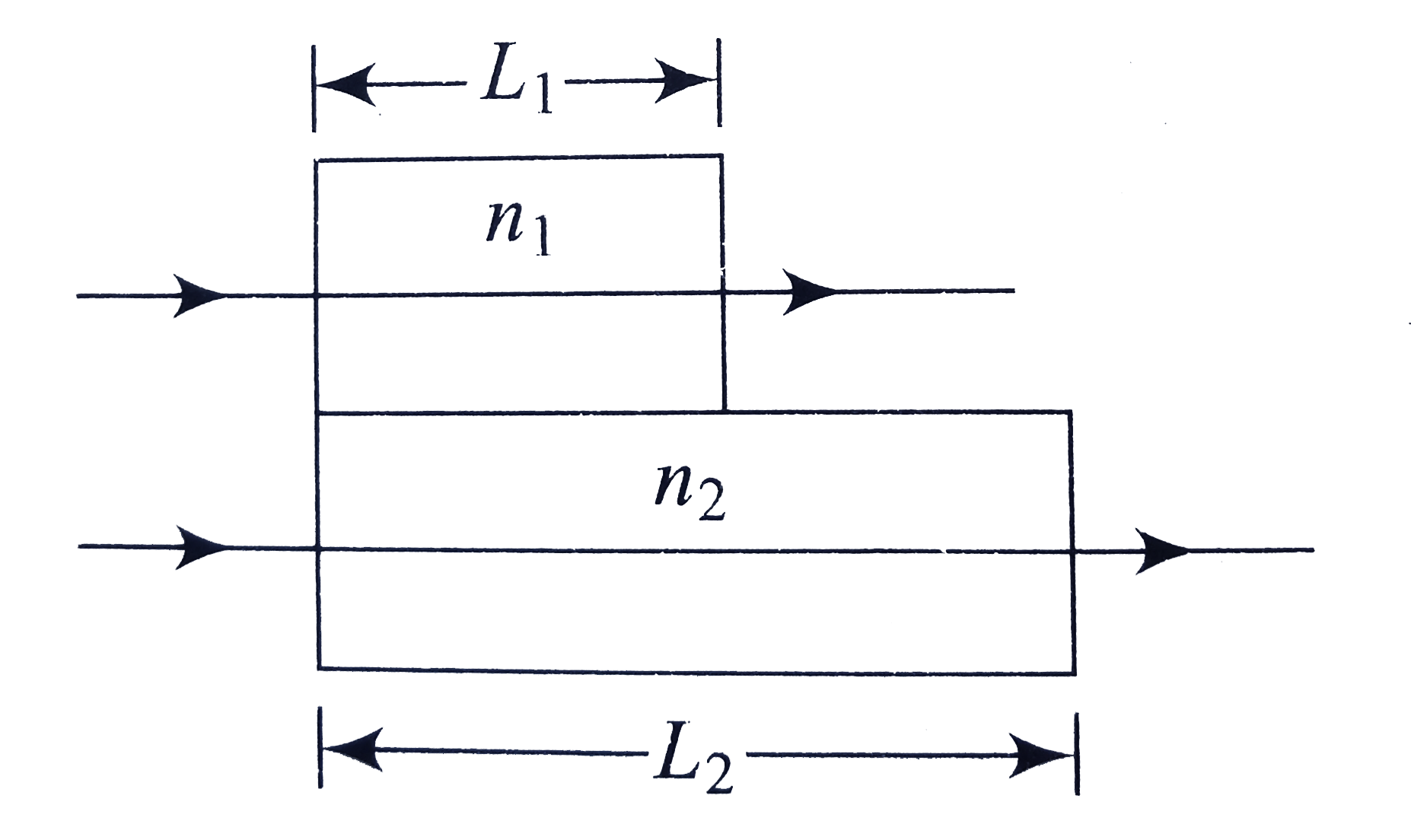
View SolutionTwo waves of light in air have the same wavelength and are intially in phase. They then travel through plastic layers with thickness of L1=3.5mm and L2=5.0mm and indices of refraction n1=1.7 and n2=1.25 as shown in figure. The rays later arrive at a common point. The longest wavelength of light for which constructive interference occurs at the point is
View Solution
Knowledge Check
A ray of light travelling in a medium of refractive index μ is incident at an angle θ on a composite transparent plate consisting of 50 plates of R.I1.01μ,1.02μ,1.03μ………,1.50μ . The ray emerges from the composite plate into a medium of refractive index 1.6μ at angle 'x' . Then :
Asin x = (1.011.5)50sinθBsin x = 58sinθCsin x = 85sinθDsin x = (1.51.01)50sinθTwo waves of light in air have the same wavelength and are intially in phase. They then travel through plastic layers with thickness of L1=3.5mm and L2=5.0mm and indices of refraction n1=1.7 and n2=1.25 as shown in figure. The rays later arrive at a common point. The longest wavelength of light for which constructive interference occurs at the point is
 A0.8μmB1.2μmC1.7μmD2.9μm
A0.8μmB1.2μmC1.7μmD2.9μmA ray of light passes through four transparent media with refractive indicesμ1,μ2,μ3 and μ4 as shown in the figure. The surfaces of all media are parallel. If the emergent ray CD is parallel to the incident ray AB, we must have
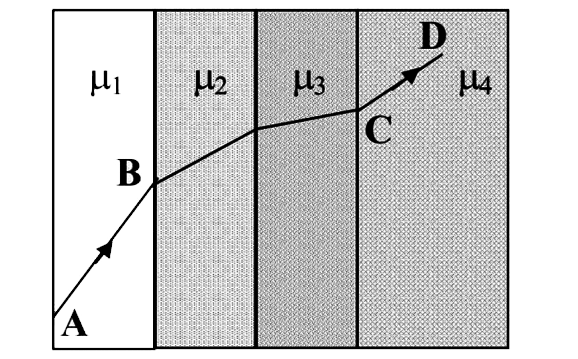 Aμ1=μ2Bμ2=μ3Cμ3=μ4Dμ4=μ1
Aμ1=μ2Bμ2=μ3Cμ3=μ4Dμ4=μ1
A ray of light travelling in glass (μg=3/2) is incident on a horizontal glass-air surface at the critical angle θC. If a thin layer of water (μw=4/3) is now poured on the glass-air surface. At what angle will the ray of light emerges into water at glass-water surface?
View SolutionA ray of light travelling in glass (μg=3/2) is incident on a horizontal glass-air surface at the critical angle θC. If a thin layer of water (μw=4/3) is now poured on the glass-air surface. At what angle will the ray of light emerges into water at glass-water surface?
View SolutionA ray of light passes through four transpar ent media with refractive indicesμ1,μ2,μ3 and μ4 as shown in figure. The surfaces of all media are parallel. If the emergent ray is parallel to the incident ray, we must hav
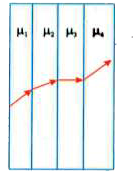
View SolutionA ray of light passes through four transpar ent media with refractive indicesμ1,μ2,μ3 and μ4 as shown in figure. The surfaces of all media are parallel. If the emergent ray is parallel to the incident ray, we must hav

View SolutionAt what angle of incidence will the light reflected from liquid (μ=1.732) be completely polarised. Does this angle depend on the wavelength of light ?
View Solution
