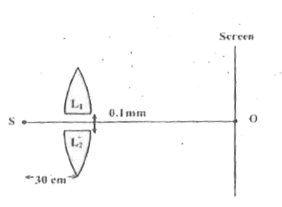
In figure S is a monochromatic point source emitting light of wavelength λ=500nm. A thin lens of circular shape and focal length 0.10m is cut into two identical halves L1 and L2 by a plane passing through a doameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5mm. The distance along the axis from A to L1 and L2 is 0.15m, while that from L1 and L2 to O is 1.30m. The screen at O is normal to SO.
(a) If the 3rd intensity maximum occurs at point P on screen, find distance OP.
(b) If the gap between L1 and L2 is reduced from its original value of 0.5mm, will the distance OP increases, devreases or remain the same?

The correct Answer is:B
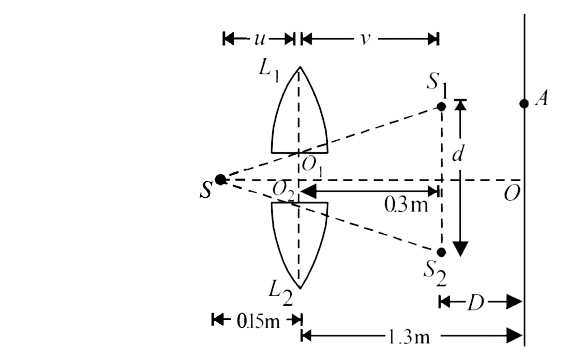
(i) In this case, the two identical halves of convex lens will create two separate images S1 and S2 of the source S. These images (S9(1)andS2) will behave as two coherent sources and the further dealing will be in accordance to Young's double slit experiment.
For lens L1
The object is S
u=−0.15m, v=?, f=+0.1m
1v−1u=1f⇒1v=1f+1u=10.1+1−0.15 ⇒ v=0.3m
△SO1O2 and △SS1S2 are similar. Also the placement of O1 and O2 are symmetrical to S
∵S1S2O1O2=u+vu
⇒S1S2=(u+v)(O1O2)u=(0.15+0.3)(0.15)×0.5×10−3
S1S2=d=1.5×10−3m ∵D=1.3−0.3=1m
The fringe width
β=λDd=500×10−9×11.5×10−3=13×10−3
∵ Therefore, OA=3β=3×13×10−3m=10−3
(ii) If the gap between L1 and L2 i.e., O1O2 is reduced. Then d will be reduced. Then the fringe width will increase and hence OA will increase.
Topper's Solved these Questions
Similar Questions
S is a monochromatic point source emitting light of wavelength l = 500 nm. A thin lens of circular shape and of focal length 0.10 m is cut into two identical halves L1 and L2 by a plane passing through a diameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5 mm. The distance along the axis from S to L1 and L2 is 0.15 m, while that from L1 and L2 to O is 1.30 m. The screen at O is normal to SO. If the third intensity maximum occurs at point A on the screen, find the distance OA.
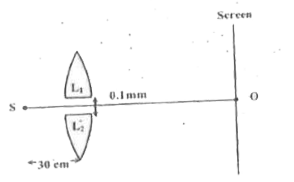
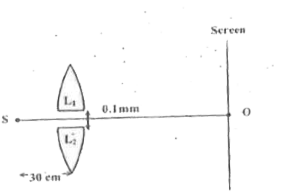
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q0.25 mm
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If a symmetrical bi-concave thin lens is cut into two identical halves, and they are placed in different ways as shown, then
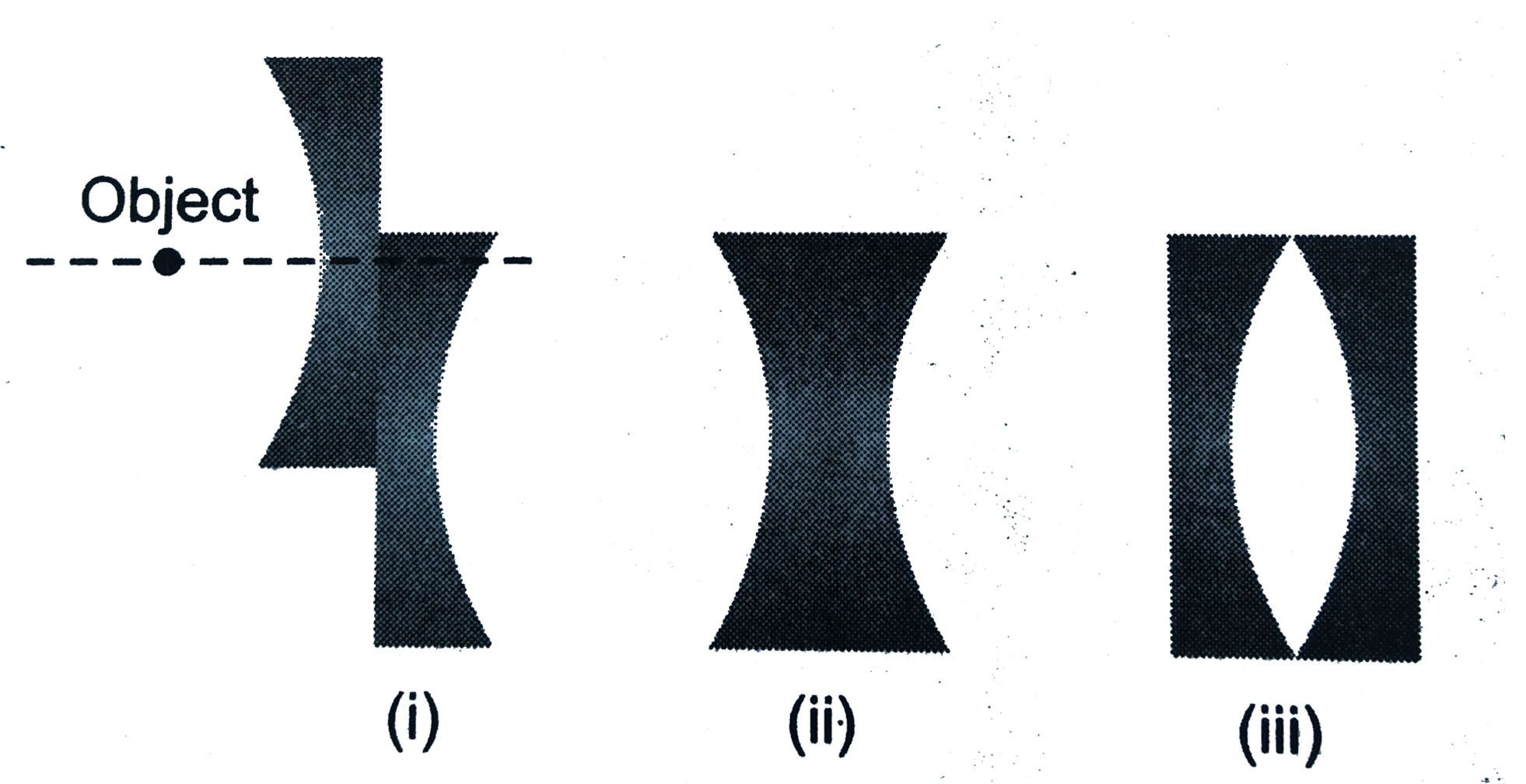 Athree images will be formed in case (ii)Bthree images will be formed in case (i)Cthe ratio of focal lengths in (ii) and (iii) is 1Dthe ratio of focal lengths in (ii) and (iii) is 2
Athree images will be formed in case (ii)Bthree images will be formed in case (i)Cthe ratio of focal lengths in (ii) and (iii) is 1Dthe ratio of focal lengths in (ii) and (iii) is 2 - Question 2 - Select One
If a equiconvex lens of focal length f is cut into two halves by a plane perpendicular to the principal axis, then
AThe focal length of each half becomesf2BThe focal length of each half becomes 2fCThe focal length of each half remains fDThe focal length of each half becomes f4 - Question 3 - Select One
Two independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Phase difference between the light waves 0.1 mm from along the screen, where intensity is half the maximum value, is
 A) tt/2Bk/3Ctt/4Dir/6
A) tt/2Bk/3Ctt/4Dir/6
Two independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Distance of a point from O, at which the sixth order minimum is formed, will be
 View Solution
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
QDistance between the images Si and S2 will be
 View Solution
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Fringe width is nearly
 View Solution
View SolutionIf distance of a point (x1,y1) from each of two lines L1 and L2, through the orign , is δ, then joint equation of L1 and L2 is
View SolutionA thin rod of mass M and length L is bent into a circular ring. The expression for moment of inertia of ring about an axis passing through its diameter is
View Solution

