In Figure, two isotropic point sources S1 and S2 emit light in phase at wavelength λ and at the same amplitude. The sources are separated by distance 2d=6.00λ. They lie on an axis that is parallel to an x axis, which runs along a viewing screen at distance D=20.0λ. The origin lies on the perpendicular bisector between the sources. The figure shows two rays reaching point P on the screen, at position xP. (a) At what value of xP do the rays have the minimum possible phase difference? (b) What multiple of λ gives that minimum phase difference? (c) At what value of xP do the rays have the maximum possible phase difference? What multiple of λ gives (d) that maximum phase difference and (c) the phase difference when xP=6.00λ? (f) When xP=6.00λ, is the resulting intensity at point P maximum, minimum, intermediate but closer to maximum, or intermediate but closer to minimum?
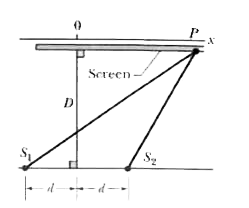
(a) 0, (b) 0, (C) ∞, (d) 12p, (e) 3.6p, (f) “intermediate” but closer to a minimum than to a maximum
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
66 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
23 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT
6 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
The intensity ratio of the two interfering beams of light is m. What is the value of Imax−Imin/Imax+Imin?
View SolutionIf white light is used in a Young's double-slit experiment, the
View SolutionThe figure shows a monochromatic ray of light traveling across parallel interfaces, from an original material a, through layers of materials b and c, and then back into material a. Rank the materials according to the speed of light in them, greatest first.

View SolutionThe radius of hydrogen atom in its ground state is 5.3×10−11m. After collision with an electron, it is found to have a radius of 21.2×10−11m. What is the principal quantum number of the final state of the atom?
View SolutionA steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
View SolutionTwo coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda . The separation between the sources is 2lambda . Consider a line passing through S_(1) and perpendicular to line S_(1) S_(2) . Find the position of farthest and nearest minima. .
View SolutionTwo monochromatic coherent point sources S_(1) and S_(2) are separated by a distance L. Each sources emits light of wavelength lambda , where L gt gt lambda . The line S_(1) S_(2) when extended meets a screen perpendicular to it at point A. Then
View SolutionTwo coherent sources emit light of wavelength lambda . Separation between them, d = 4 lambda . If a detector moves along the y-axis, what is the maximum number of minima observed? If the detector moves along 'x-axis beginning from S_(2) , the maximum number of minima observed is
View SolutionTwo coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
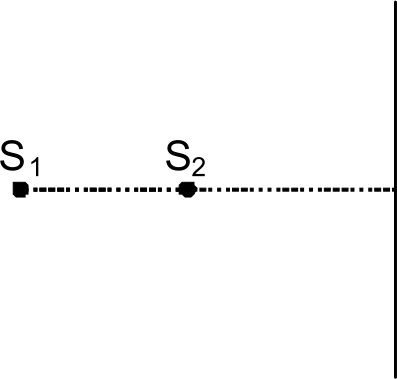
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
View SolutionTwo coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda .The separation between the sources is 2 lambda .The smallest distance from S_(2) on a line passing through S_(2) and perpendicular to S_(1)S_(2) where a minimum intensity occurs is :
View Solution
In Figure, two radio- frequency point sources S1 and S2 separated by distance d = 1.8 m, are radiating in phase with λ=0.50m. A detector moves in a large circular path around the two sources in a plane contain- ing them. How many (a) maxima and (b) minima does it detect?
View SolutionFour monochromatic and coherent sources of light, emitting waves in phase of wavelength lambda , are placed at the points x = 0, d = 2d and 3d on the x-axis. Then
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance >. Each source emits light of wavelength λ where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Which of the following is correct ?
View SolutionThe figure shows two points source which emit light of wavelength lambda in phase with each other and are at a distance d = 5.5 lambda apart along a line which is perpendicular to a large screen at a distance L from the centre of the source. Assume that d is much less than L. Which of the following statement is (are) correct ?
View SolutionFour monochronic and coherent sources of light , emitting waves in phase of wavelength λ , are placed at the points x = 0 d,2d and 3d on the x - axis .Then
View Solution
