In tae-kwon-do, a hand is slammed down onto a target at a speed of 13 m/s and comes to a stop during the 5.5 ms collision. Assume that during the impact the hand is independent of the arm and has a mass of 0.70 kg. What are the magnitudes of the (a) impulse and (b) average force on the hand from the target?
The correct Answer is:(a)9.1 N.s ; (b) N
To solve the problem, we need to calculate the impulse and the average force exerted on the hand during the collision with the target. Let's break this down step by step.
Step 1: Calculate the initial momentum of the hand.
The initial momentum (p_initial) can be calculated using the formula:
pinitial=m⋅v
where:
- m=0.70kg (mass of the hand)
- v=13m/s (initial velocity of the hand)
Calculating this gives:
pinitial=0.70kg⋅13m/s=9.1kg m/s
Step 2: Calculate the final momentum of the hand.
Since the hand comes to a stop after hitting the target, the final velocity (v_final) is 0 m/s. Thus, the final momentum (p_final) is:
pfinal=m⋅vfinal=0.70kg⋅0m/s=0kg m/s
Step 3: Calculate the change in momentum (impulse).
Impulse (J) is defined as the change in momentum:
J=pfinal−pinitial
Substituting the values we found:
J=0−9.1kg m/s=−9.1kg m/s
Since impulse is a magnitude, we take the absolute value:
|J|=9.1N s
Step 4: Calculate the average force exerted on the hand.
The average force (F) can be calculated using the formula:
F=JΔt
where Δt is the time duration of the collision. Given Δt=5.5ms=5.5×10−3s:
F=9.1N s5.5×10−3s
Calculating this gives:
F=9.15.5×10−3≈1654.55N
Rounding this gives:
F≈1.7×103N
Final Answers:
(a) Impulse = 9.1 N s
(b) Average Force = 1.7 × 10³ N
---
The initial momentum (p_initial) can be calculated using the formula:
pinitial=m⋅v
where:
- m=0.70kg (mass of the hand)
- v=13m/s (initial velocity of the hand)
pinitial=0.70kg⋅13m/s=9.1kg m/s
Since the hand comes to a stop after hitting the target, the final velocity (v_final) is 0 m/s. Thus, the final momentum (p_final) is:
pfinal=m⋅vfinal=0.70kg⋅0m/s=0kg m/s
Impulse (J) is defined as the change in momentum:
J=pfinal−pinitial
Substituting the values we found:
J=0−9.1kg m/s=−9.1kg m/s
Since impulse is a magnitude, we take the absolute value:
|J|=9.1N s
The average force (F) can be calculated using the formula:
F=JΔt
where Δt is the time duration of the collision. Given Δt=5.5ms=5.5×10−3s:
F=9.1N s5.5×10−3s
F=9.15.5×10−3≈1654.55N
Rounding this gives:
F≈1.7×103N
(a) Impulse = 9.1 N s
(b) Average Force = 1.7 × 10³ N
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
Jumping up before the elevator hits. After the cable snaps and the safety system fails, an elevator cab free-falls from a height of 36 m. During the collision at the bottom of the elevator shaft, a 90 kg passenger is stopped in 5.0 ms. (Assume that neither the passenger nor the cab rebounds.) What are the magnitudes of the (a) impulse and (b) average force on the passenger during the collision? If the passenger were to jump upward with a speed of 7.0 m/s relative to the cab floor just before the cab hits the bottom of the shaft, what are the magnitudes of the (c) impulse and (d) average force (assuming the same stopping time)?
View SolutionIn a common but dangerous prank, a chair is pulled away as a person is moving downward to sit on it, causing the victim to land hard on the floor. Suppose the victim falls by 0.50 m, the mass that moves downward is 75 kg, and the collision on the floor lasts 0.088 s. What are the magnitudes of the (a) impulse and (b) average force acting on the victim from the floor during the collision?
View Solution
Knowledge Check
- Question 1 - Select One
The head of a hammer (m = 1.5 kg) moving at 4.5 m/s strikes a nail and bounces back with the same speed after an elastic collision lasting 0.075 s. What is the magnitude of the average force the hammer exerts on the nail?
A6.8 NB90 NC60 ND180 N - Question 2 - Select One
A landing airplane makes contact with the runway with a speed of 78.0 m/s and moves towards the south. After 18.5 seconds, the airplane comes to rest. What is the average acceleration of the airplane during the landing ?
A2.11m/s2, northB4.22 m/s2 , northC2.11m/s2 , southD4.22m/s2, south
In Fig. 5-45, a crate of mass m = 115 kg is pushed at constant speed up a frictionless ramp (θ=30.0∘) by a horizontal force →F. What are the magnitudes of (a) →F and (b) the force on the crate from the ramp ?
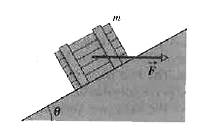 View Solution
View SolutionFigure shows a 0.300 kg baseball just before and just after it collides with a bat. Just before, the ball has velocity →v1 of magnitude 12.0 m/s and angle θ1=35.0∘ Just after, it is traveling directly upward with velocity →v2 of magnitude 10.0 m/s The duration of the collision is 2.00 ms. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the impulse on the ball from the bat? What are the (c) magnitude and (d) direction of the average force on the ball from the bat?
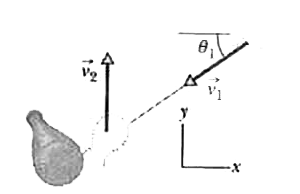 View Solution
View SolutionA 5.0g bullet moving at 100m/s strikes a log. Assume that the bullet undergoes uniform deceleration and stops in 6.0cm. Find (a) the time taken for the bullet to stop, (b) the impulse on the log and (c) the average force experienced by the log.
View SolutionIn February 1955, a paratrooper fell 370 m from an air plane without being able to open his chute but happened to land in snow. suffering only minor injuries. Assume that his speed at impact was 56 m/s (terminal speed), that his mass (including gear) was 85 kg, and that the magnitude of the force on him from the snow was at the survivable limit of 1.2×105 N. What are (a) the minimum depth of snow that would have stopped him safely and (b) the magnitude of the impulse on him from the snow?
View SolutionIn about 1915, Henry Sincosky of Philadelphia suspended himself from a rafter by gripping the rafter with the thumb of each hand on one side and the fingers on the opposite side (Fig. 6-35). Sincosky's mass was 79 kg. If the coefficient of static friction between hand and rafter was 0.70, what was the least magnitude of the normal force on the rafter from each thumb or opposite fingers? (After suspending himself, Sincosky chinned himself on the rafter and then moved hand-over-hand along the rafter. If you do not think Sincosky's grip was remarkable, try to repeat his stunt.)
 View Solution
View SolutionFigure 5-55 shows a man sitting in a bosun's chair that dangles from a mass-less rope, which runs over a massless, frictionless pulley and back down to the man's hand. The combined mass of man and chair is 103.0 kg. With what force magnitude must the man pull on the rope if he is to rise (a) with a constant velocity and (b) with an upward acceleration of 1.30 m/s2 ?
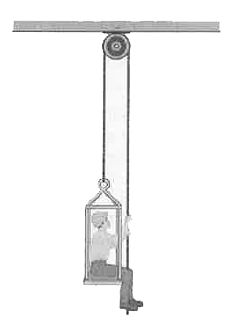 View Solution
View Solution

