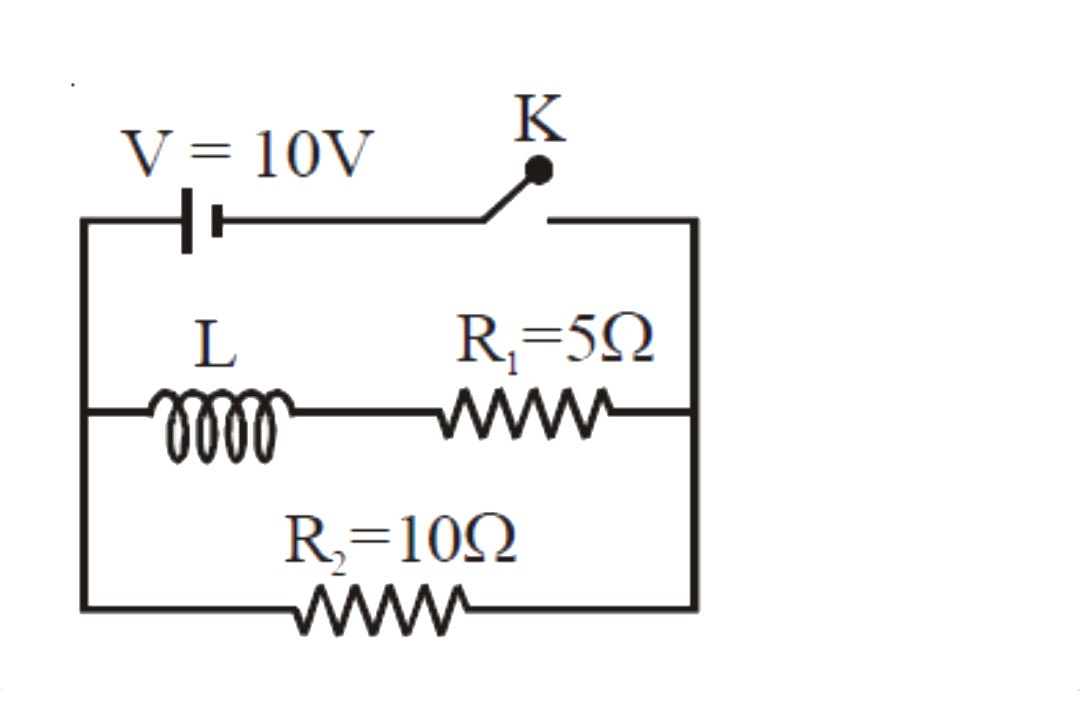
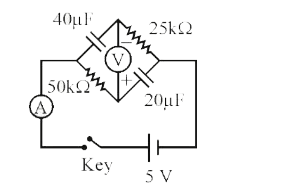
In th circuit the key (K) is closed at t=0. Find the current in ampere through the key (K) at the instant t=102ln2 sec.

Video Solution
Text Solution
The correct Answer is:2
i1 is current in the first loop
i1=4020(1−et5×10−4)=32 amp
i2 is current in the second loop
i2=4040e−t10−3=12 amp
So, total current through key (K)
i=i1+i2
=32+12=2 amp
|
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
Knowledge Check
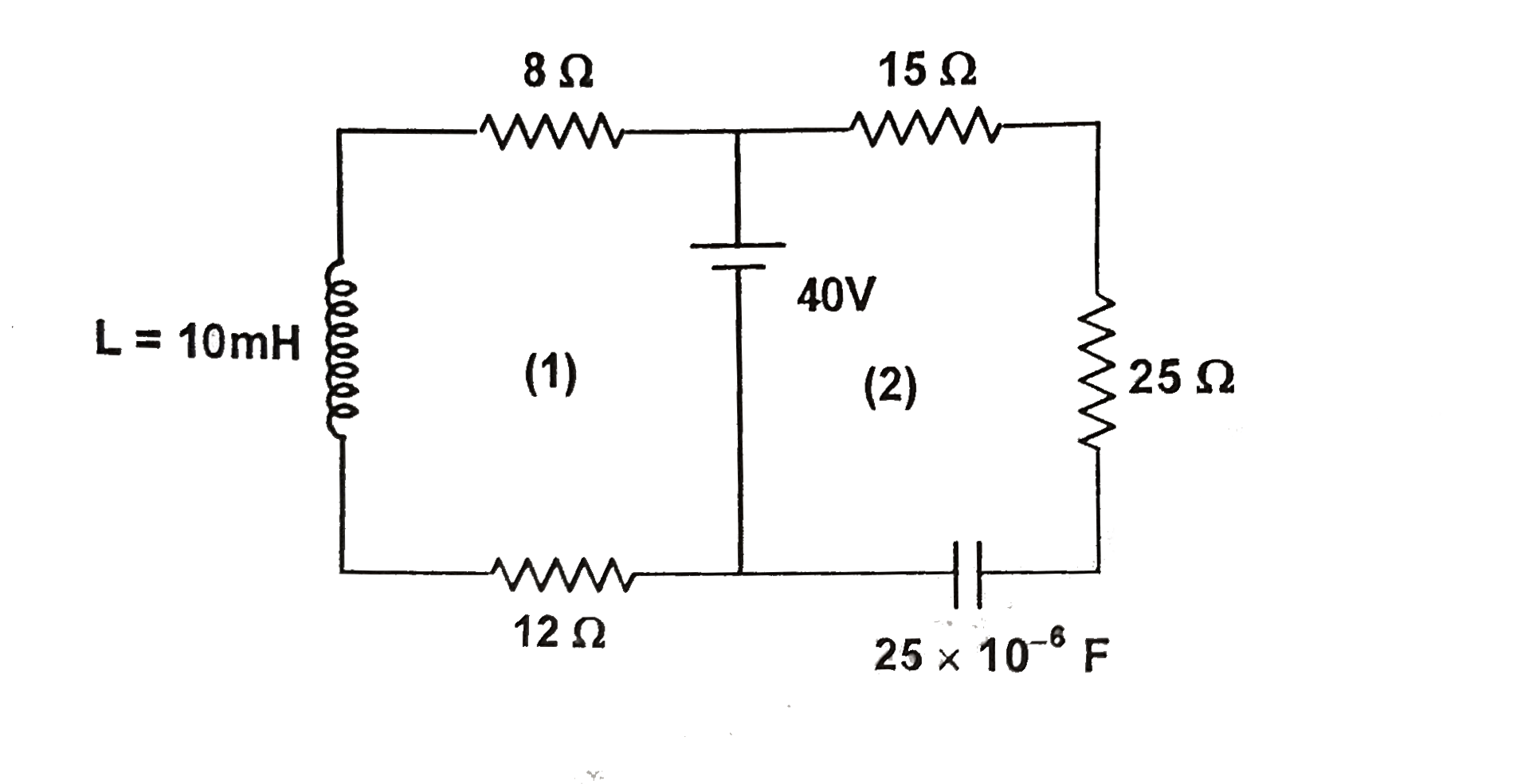
In the circuit shown the key (K) is closed at t=0, the current through the key at the instant t=10−3ln,2 is
 A2AB8AC4ADzero
A2AB8AC4ADzeroIn the circuit shows in Fig. kay K is closed at t=0, the current through the key at the instant t=10−3In2s is
 A2AB3.5AC2.5AD0
A2AB3.5AC2.5AD0In the circuit shown key is closed at t=0 with capacitor initially uncharged.
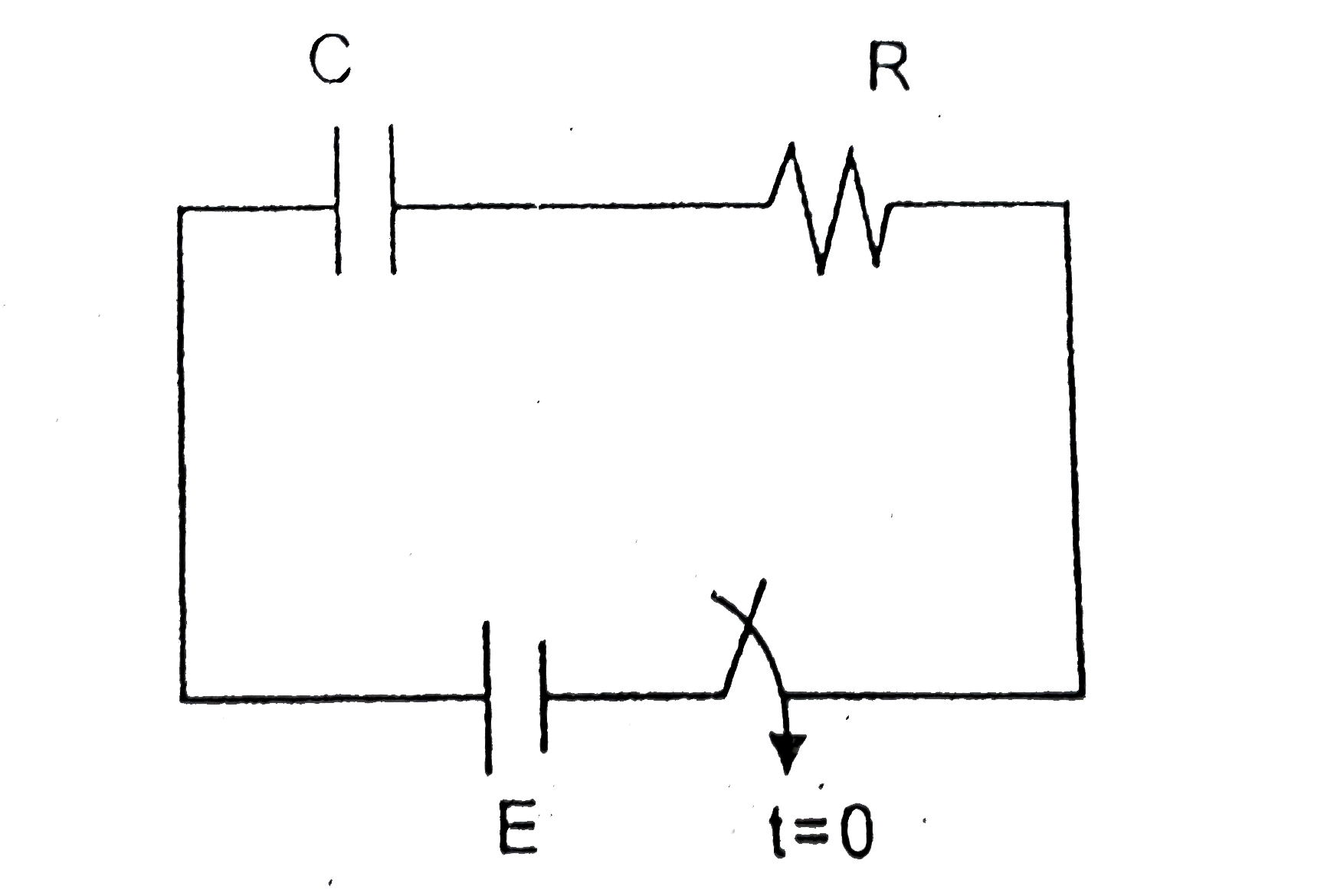 ARate of increase of capacitors energy, just after the switch is closed is E2RBMaximum power supplied by the cell is E2RCAt t=RCIn2, capacitor is charged up to half of the energy stored by it in steady stateDAt t=RCIn2, potential difference across capacitor is same that across resistor.
ARate of increase of capacitors energy, just after the switch is closed is E2RBMaximum power supplied by the cell is E2RCAt t=RCIn2, capacitor is charged up to half of the energy stored by it in steady stateDAt t=RCIn2, potential difference across capacitor is same that across resistor.
In the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionThe key 'K' is switched on at t=0. Then the currents through battery at t=0 and t=∞ are
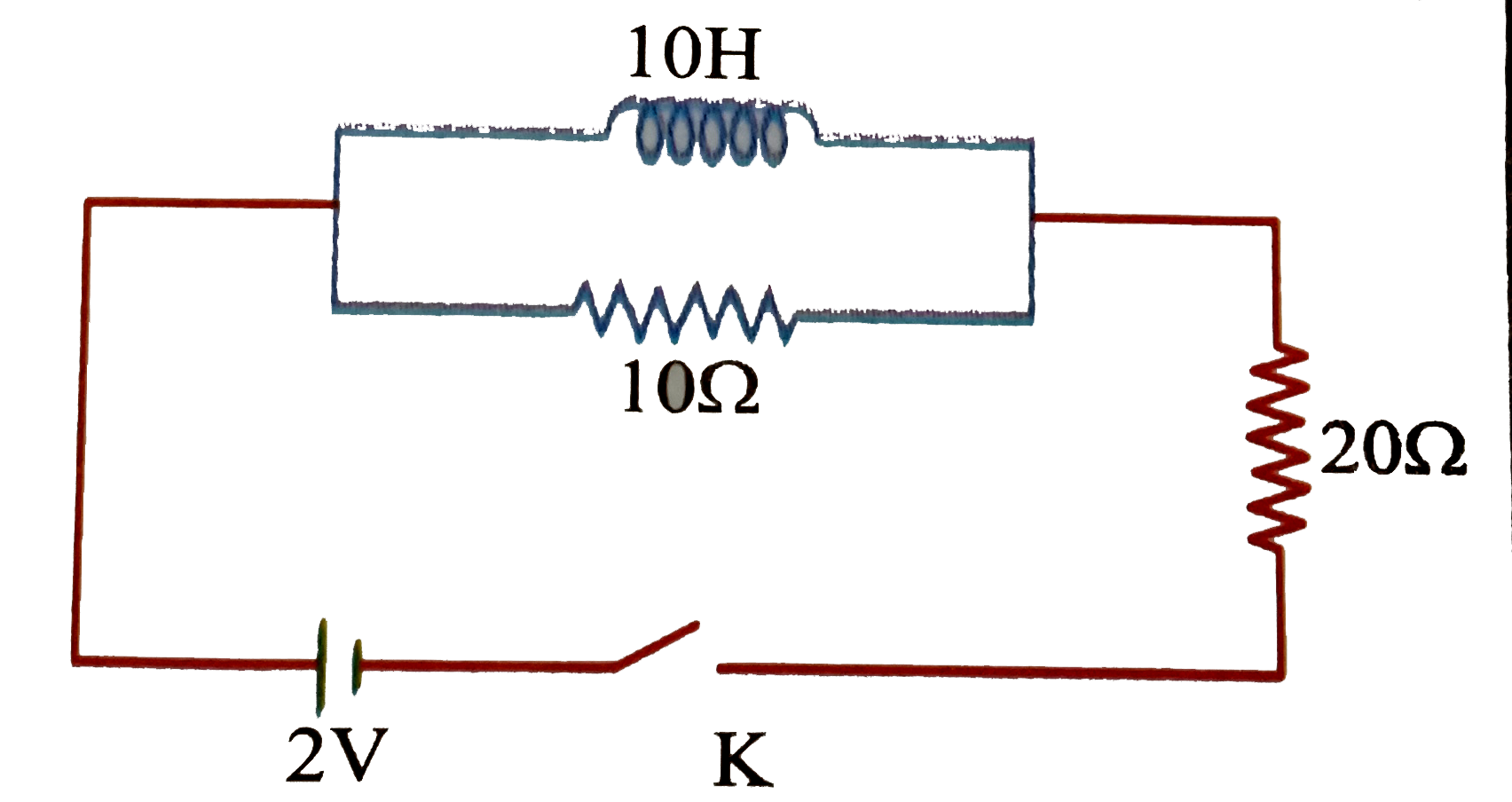
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionThe switch S of the circuit is closed at t = 0. Find the current (in Amp.) through the capacitor when the switch S is closed at t = 0

View SolutionIn the circuit shown below, the key is pressed at time t = 0. The correct statement is
View Solution