
In the arrangement shown if Fig. Pulleys are small and lught and spring are ideal and K1=25(π2)Nm, K2=2K1,K3= and K4=4K1 are the force constant of the spring. Calculate the period of small vertical oscillation of block of mass m=3kg.
In static equilibrium of block, tension in the string is exactly equal to its weight. Let a vertically downward force F be applied on the block to pull it downwards. Equilibrium is again restored when tension in the string is increased by the same amount F. Hence, total tension in the string becomes equal to (mg+F) Strings are further elongated due to extra tension F in strings, tension in each spring increases by 2F. Hence increase in elongation of springs is 2FK12FK22FK3 and 2FK4, respectively. According to geometry of the arrangement, downward displacement of the block from its equilibrium position is
y=2(2FK1+2FK2+2FK3+2FK4) ..(i)
If the block is released now, it starts to accelerate upeards due to extra tension F in the string. It means restoring force on the block is equal to F. From Eq. (i)
F=y4m(1K1+1K2+1K3+1K4)
Since acceleration of block is restoring and is directly proportional to displacement y, the block performs SHM.
Its period T=2π√displacementacceleration.
T=2π√4m(1K1+1K2+1K3+1K4)
T=4π√m(1K1+1K2+1K3+1K4)
After subsituting the values we get T=2s.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct Answer Type
29 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
In the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.

View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.

View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.

View SolutionTwo springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are k1andk2 respectively. The period of vertical oscillations of the system will be
View Solution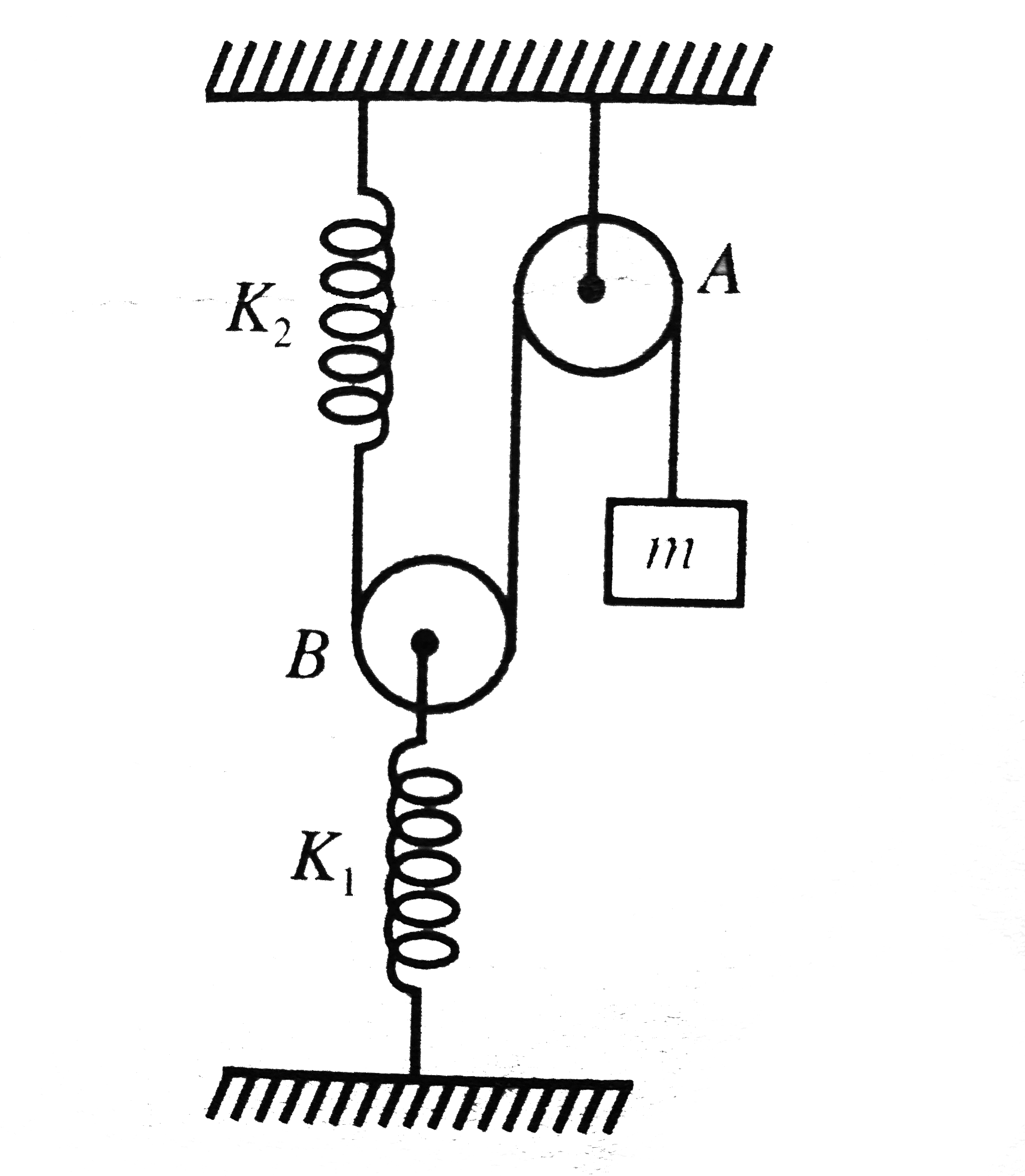
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionTwo light spring of force constants k1 and k2 and a block of mass m are in one line AB on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance CD between the spring is 60cm. If the block moves along AB with a velocity 120cm/s in between the springs, calculate the period of oscillation of the block. (take k1=1.8N/m, k2=3.2N/m, m=200g)

View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

View SolutionThe is an arrangement of pulleys as shown in figure. All the pulley are massless and frcitionless and the strings used are inextensible. Each of these springs have a spring constant k. We define the stiffness of the assembly k1 as the force required to be applied at point A for its unit displacement.
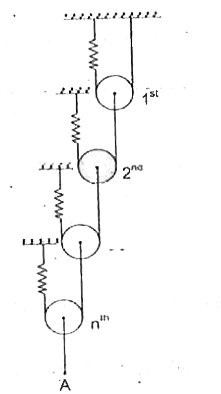
Find k1 for n=2
View SolutionThe is an arrangement of pulleys as shown in figure. All the pulley are massless and frcitionless and the strings used are inextensible. Each of these springs have a spring constant k. We define the stiffness of the assembly k1 as the force required to be applied at point A for its unit displacement.
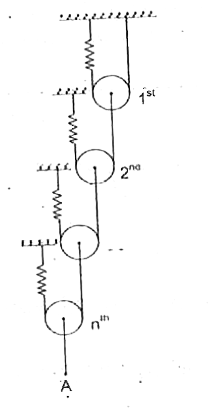
What will he the most probable value of k1 for n =3
View Solution
