In the arrangement shown in Fig. the ball and the block have the same mass m=1kg each, θ=60∘ and length l=2.50m. Coefficient of friction between the block and the floor is 0.5. When the ball is released from the position shown in Fig. it collides with the block and the block stops after moving a distance 2.50m.

The velocity of block just after collision is
10m/s
5m/s
2.5m/s
3m/s
The correct Answer is:B
When ball is released, it moves along a vertical circle with centre at A. Kinetic energy of ball just before collision is equal to loss of its potential energy from point of release to the point of collision. Therefore, velocity v1 of ball, just before collision, is given by
12mv21mg(l−lcosθ)⇒v1=5m/s
After collision, the block starts to move towards right. But it is retarded by force of friction and ultimately it comes to rest. According to law of conservation of energy,
Kinetic energy of the block just after collision = Work done by it against friction.
Therefore, its velocity v, just after collision is given by
12mv22=μmgs
where m=0.54 and s=2.50m∴v2=5m/s
Coefficient of restitution e=v2−v1u2−u1
where u2=0,u1=5ms and v1=(5−5e) …………i
Applying law of conservation momentum.
mu1+mu2=mv1+mv2
5m+(m×0)=mv1+5m or v1=0
substituting in eqn i we get e=1
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
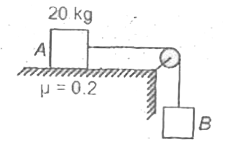
In the figure shown, the coefficient of static friction between the block A of mass 20 kg and horizontal table is 0.2. What should be the minimum mass of hanging block just beyond which blocks start moving?
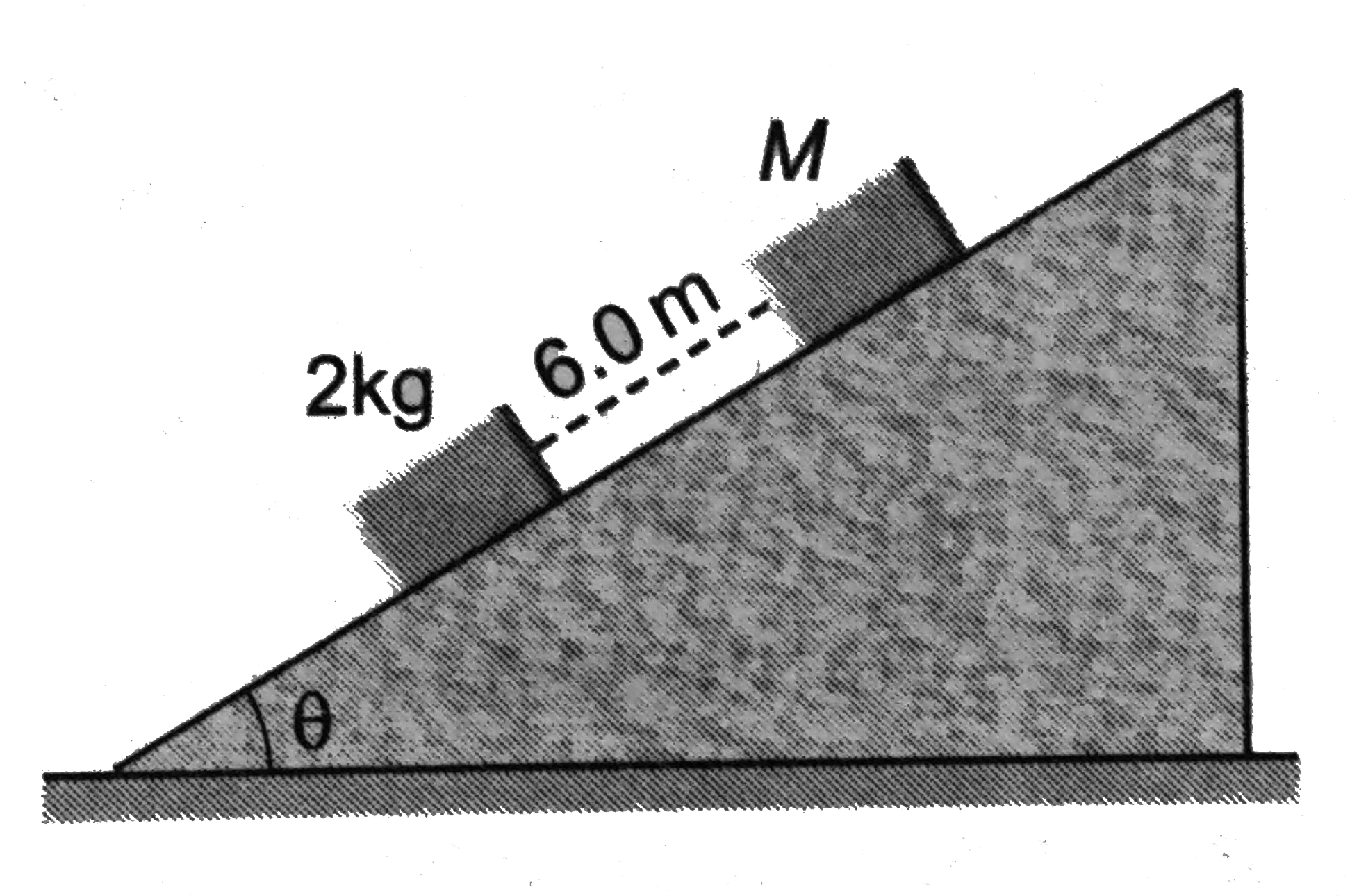
View SolutionTwo blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
View Solution
Knowledge Check
In the arrangement shown in Fig. the ball and the block have the same mass m=1kg each, θ=60∘ and length l=2.50m. Coefficient of friction between the block and the floor is 0.5. When the ball is released from the position shown in Fig. it collides with the block and the block stops after moving a distance 2.50m.
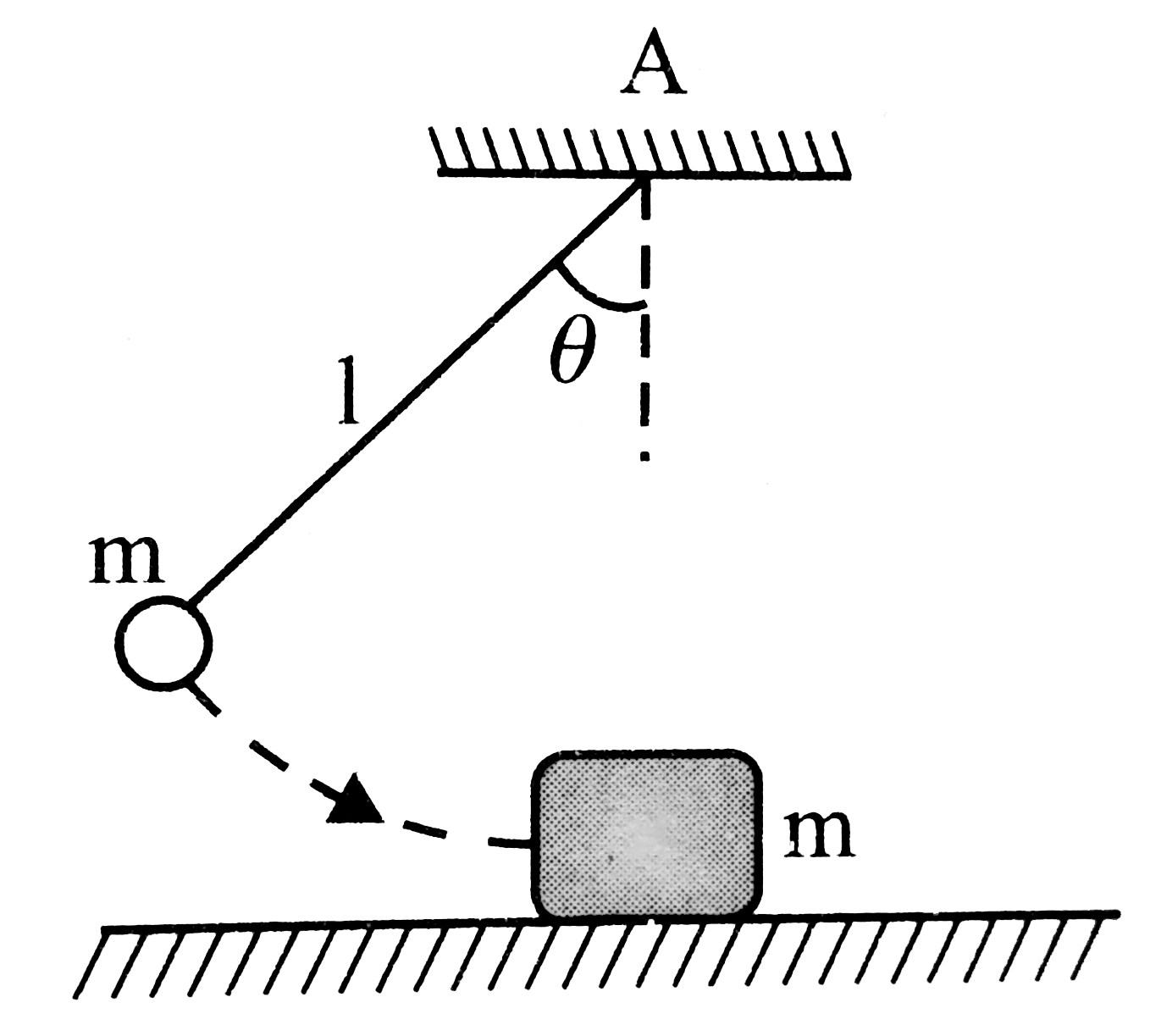
The coefficient of restitution for collision between the ball and the block isA0.5B0.75C1.0D0.3The ball is released when the string is horizontal. The collision between the ball and the block is head - on elastic. The velocities of the ball and the block immediately after collision
 A23√2gL,13√2gLB−23√2gL,13√2gLC23√2gL,−13√2gLD−23√2gL,−13√2gL
A23√2gL,13√2gLB−23√2gL,13√2gLC23√2gL,−13√2gLD−23√2gL,−13√2gLIn Fig. 7.149 , coefficient of friction between the block and the floor is μ . Force F that will move the block on the floor with a uniform speed is :
 A(μsinθ+cosθ)mgB(μsinθ−cosθ) mgCμmgcosθ−μsinθDμmgsinθ−μcosθ
A(μsinθ+cosθ)mgB(μsinθ−cosθ) mgCμmgcosθ−μsinθDμmgsinθ−μcosθ
In Fig. 6-37, a block of mass m = 5.0 kg is at rest on a ramp. The coefficient of static friction between the block and ramp is not known. Find the magnitude of the net force exerted by the ramp on the block.

View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionThe block of mass m is in contact with a moving cart as shown in the figure.The coefficient of friction between the block and the cart is . The acceleration a of the cart that will prevent the block from falling is

View SolutionA block of mass 50 kg is projected horizontal on a rough horizontal floor. The coefficient of friction between the block and the floor is 0.1. The block strikes a light spring of stiffness k=100N/m with a velocity 2m/s, the maximum compression of the spring is

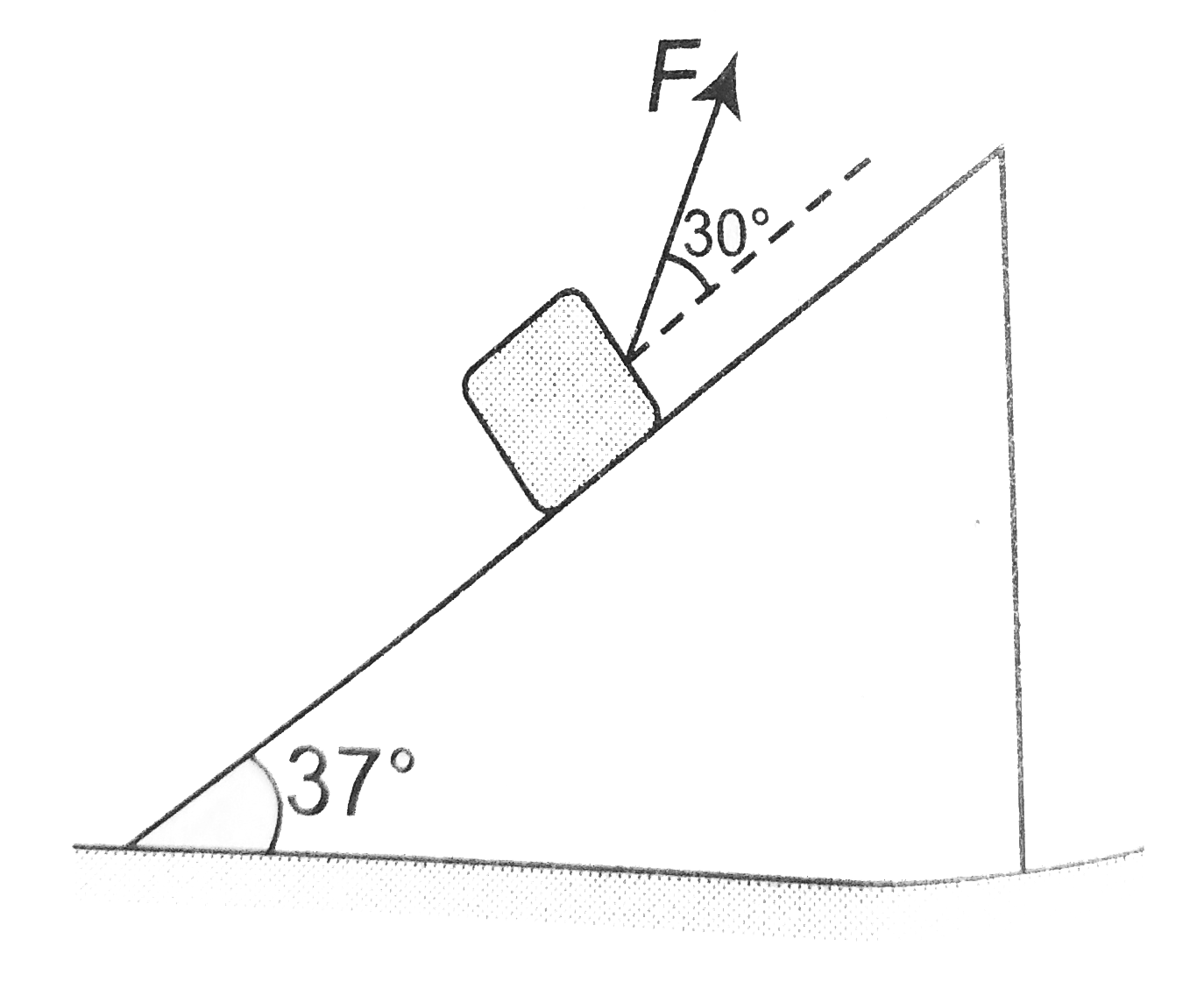
View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
View Solution
