In the arrangement shown in Fig. the ball and the block have the same mass m=1kg each, θ=60∘ and length l=2.50m. Coefficient of friction between the block and the floor is 0.5. When the ball is released from the position shown in Fig. it collides with the block and the block stops after moving a distance 2.50m.
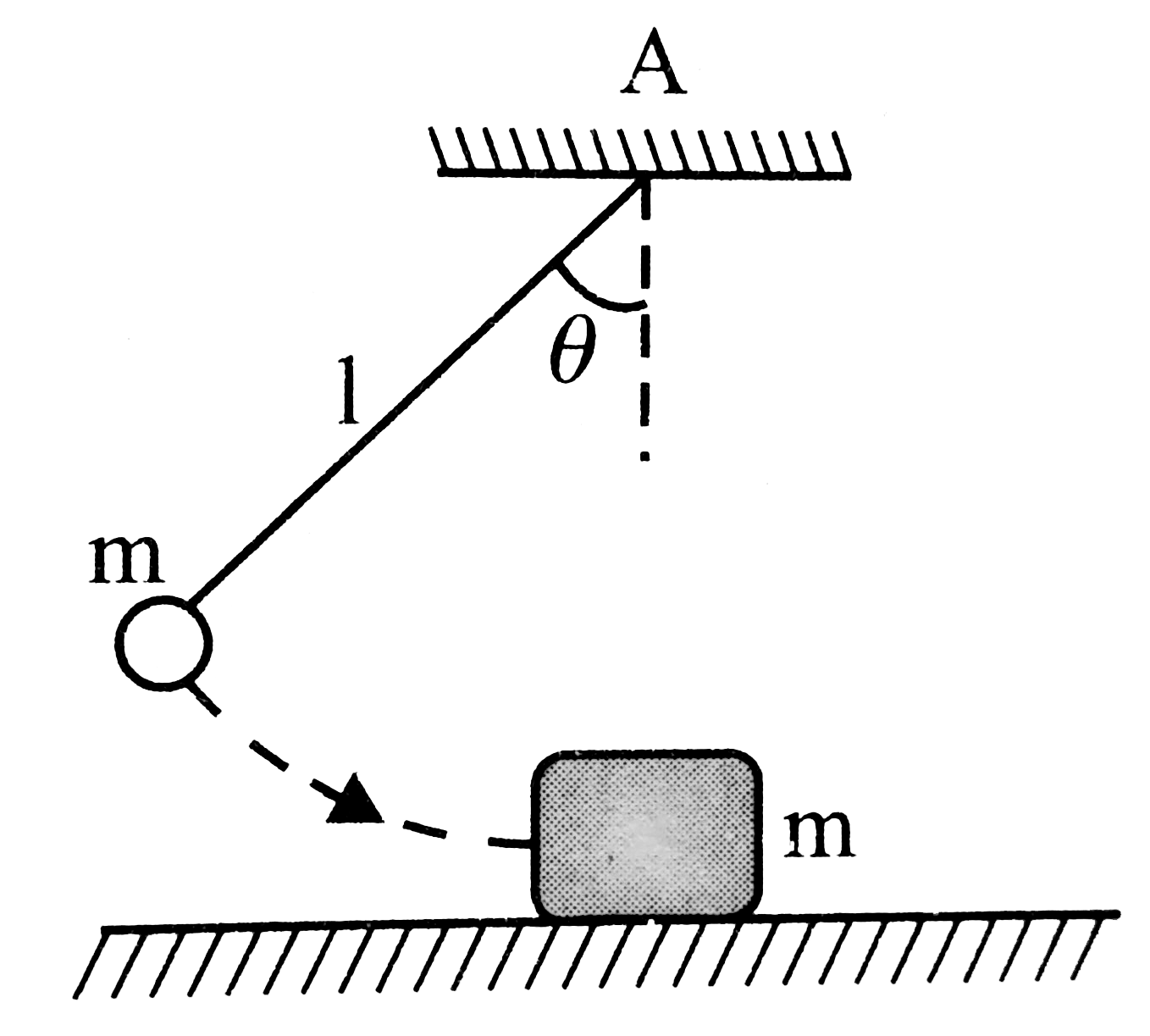
The coefficient of restitution for collision between the ball and the block is
0.5
0.75
1.0
0.3
The correct Answer is:C
When ball is released, it moves along a vertical circle with centre at A. Kinetic energy of ball just before collision is equal to loss of its potential energy from point of release to the point of collision. Therefore, velocity v1 of ball, just before collision, is given by
12mv21mg(l−lcosθ)⇒v1=5m/s
After collision, the block starts to move towards right. But it is retarded by force of friction and ultimately it comes to rest. According to law of conservation of energy,
Kinetic energy of the block just after collision = Work done by it against friction.
Therefore, its velocity v, just after collision is given by
12mv22=μmgs
where m=0.54 and s=2.50m∴v2=5m/s
Coefficient of restitution e=v2−v1u2−u1
where u2=0,u1=5ms and v1=(5−5e) …………i
Applying law of conservation momentum.
mu1+mu2=mv1+mv2
5m+(m×0)=mv1+5m or v1=0
substituting in eqn i we get e=1
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
In the arrangement shown in Fig. the ball and the block have the same mass m=1kg each, θ=60∘ and length l=2.50m. Coefficient of friction between the block and the floor is 0.5. When the ball is released from the position shown in Fig. it collides with the block and the block stops after moving a distance 2.50m.
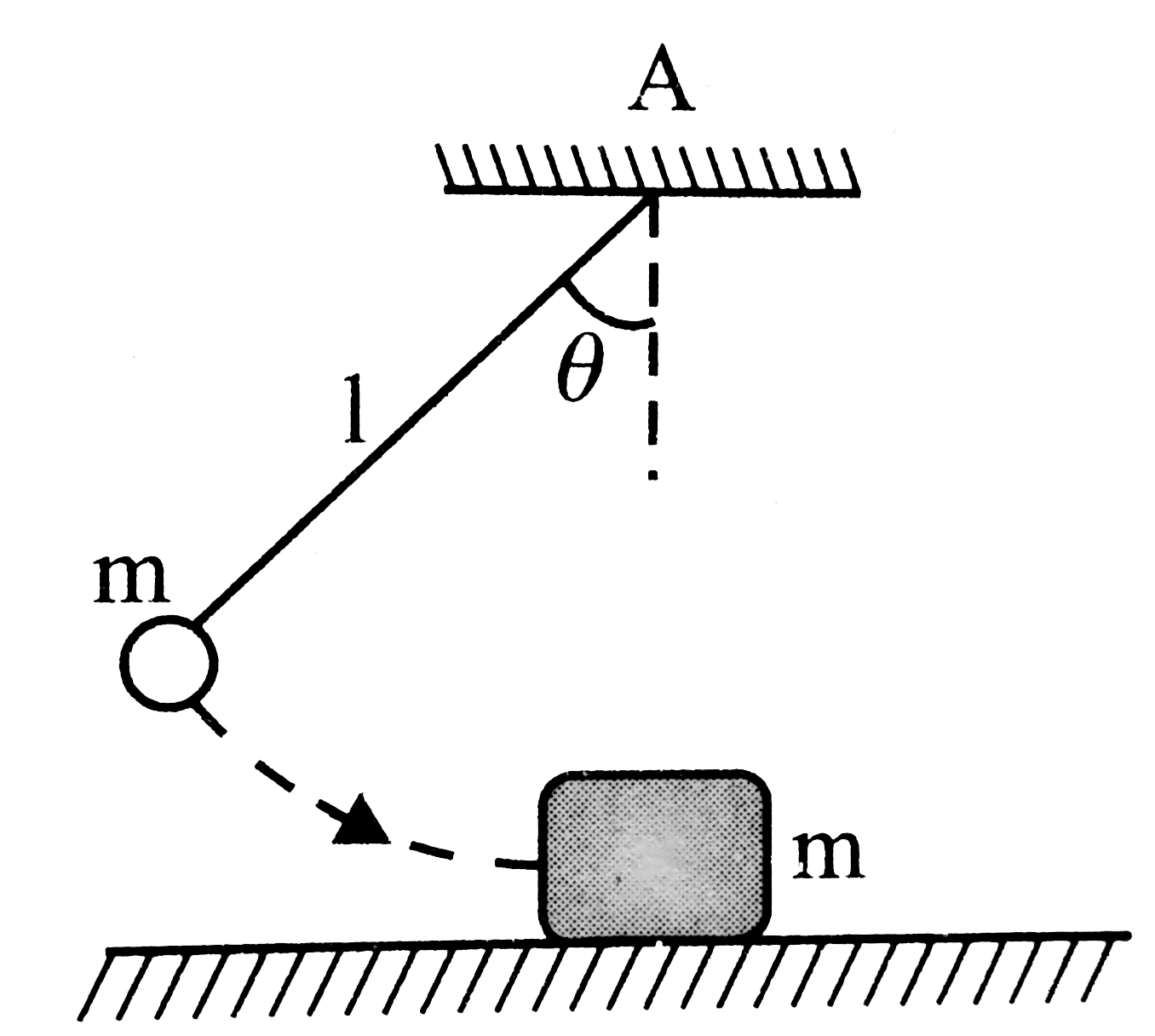
The velocity of block just after collision is
View SolutionA ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
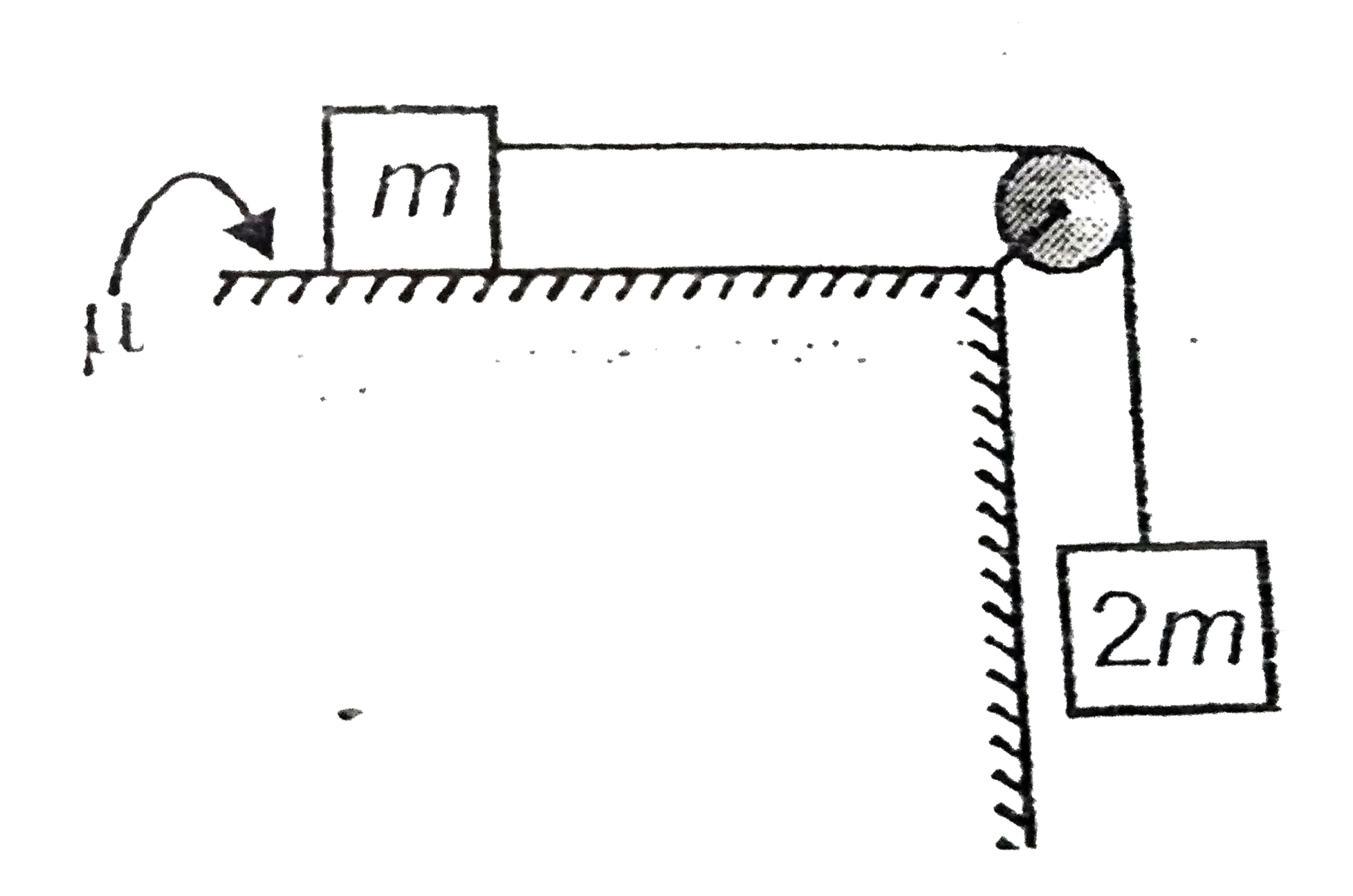
View SolutionConsider the system shown in the figure. Coefficient of friction between the block and table is μ=0.5. The system is released from rest. Find the work done by friction, when the speed of block is 10 m/s (m=1kg)
View SolutionA block of mass'm' is resting on the floor of a lift. The coefficient of friction between the block and the floor is μ. When the lift is falling freely, the limiting frictional force between block and surface is
View SolutionIn the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.

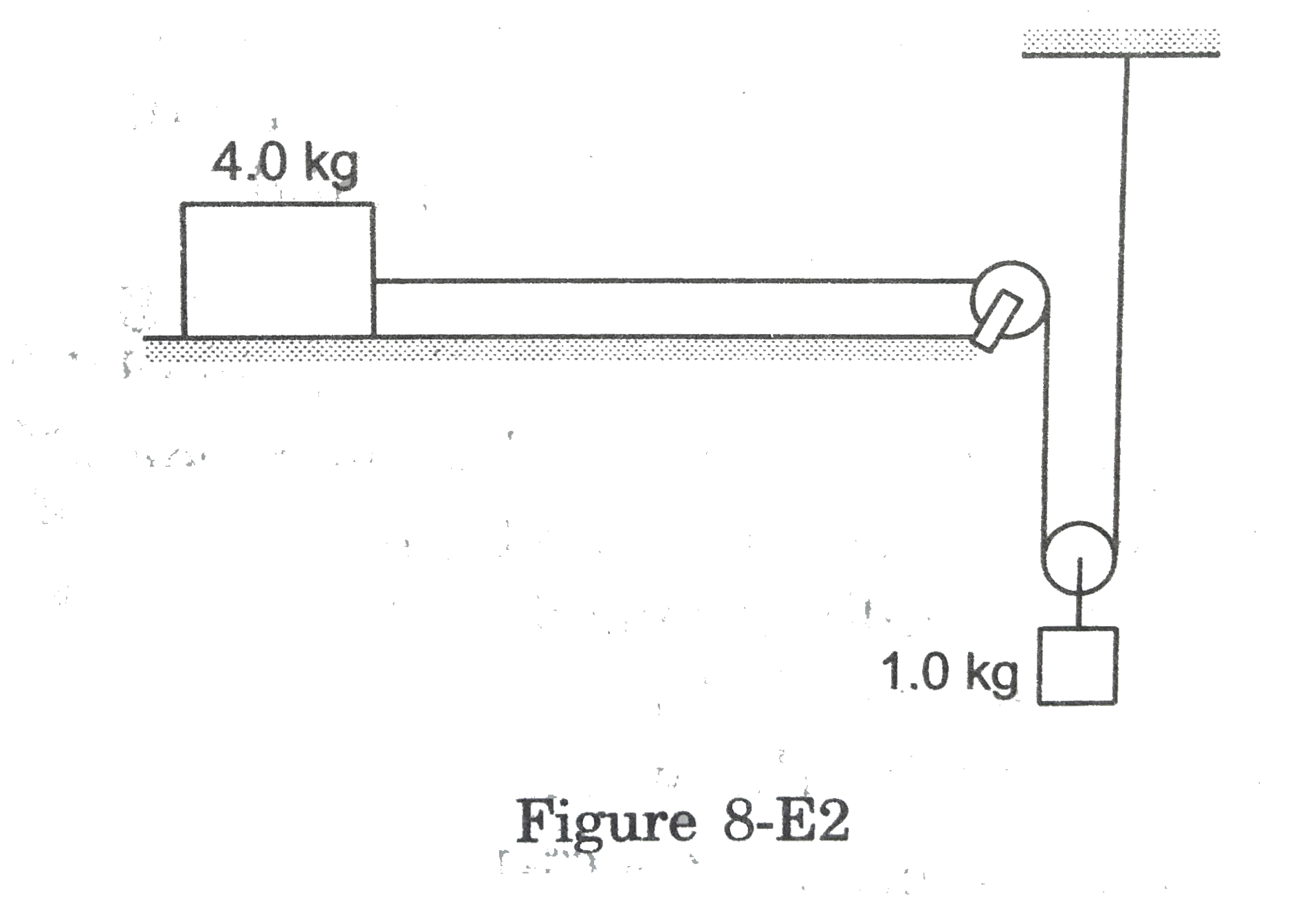
View SolutionConsider the situatioin shown in figure. The system is released from rest and the block of mass 1.0 kg is found to have a speed 0.3 m/s ater it has descended thrugh a distance of 1 m. find the coefficient of kinetic friction between the block and the table.
View SolutionA block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View Solution
