In the arrangement shown in figure the cylinder of mass M is at rest on an incline. The string between the cylinder and the pulley (P) is horizontal. Find the minimum coefficient of friction between the incline and the cylinder which can keep the system in equilibrium. Also find the mass of the block. Assume no friction between the pulley (P) and the string.
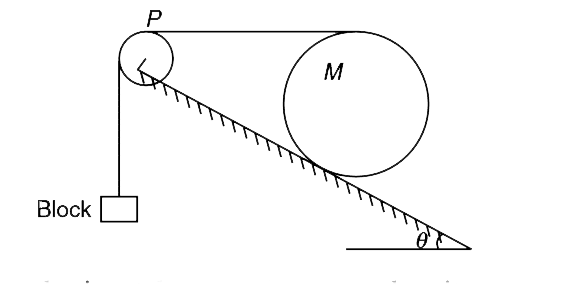
The correct Answer is:μmin=sinθ1+cosθ;mblock=Msinθ1+cosθ
Step by step video, text & image solution for In the arrangement shown in figure the cylinder of mass M is at rest on an incline. The string between the cylinder and the pulley (P) is horizontal. Find the minimum coefficient of friction between the incline and the cylinder which can keep the system in equilibrium. Also find the mass of the block. Assume no friction between the pulley (P) and the string. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
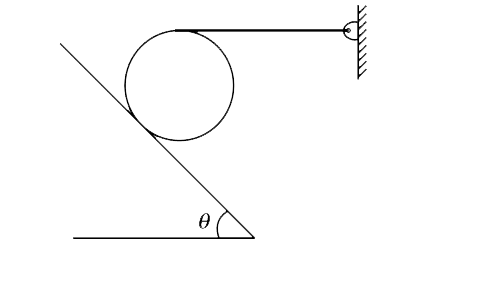
A horizontal stick of mass m has its right end attached to a pivot on a wall, while its left end rests on the top of a cylinder of mass m which in turn rests on an incline plane inclined at an angle θ. The stick remains horizontal. The coefficient of friction between the cylinder and both the plane and the stick is μ. Find the minimum value of μ as function of θ for which the system stays in equilibrium.
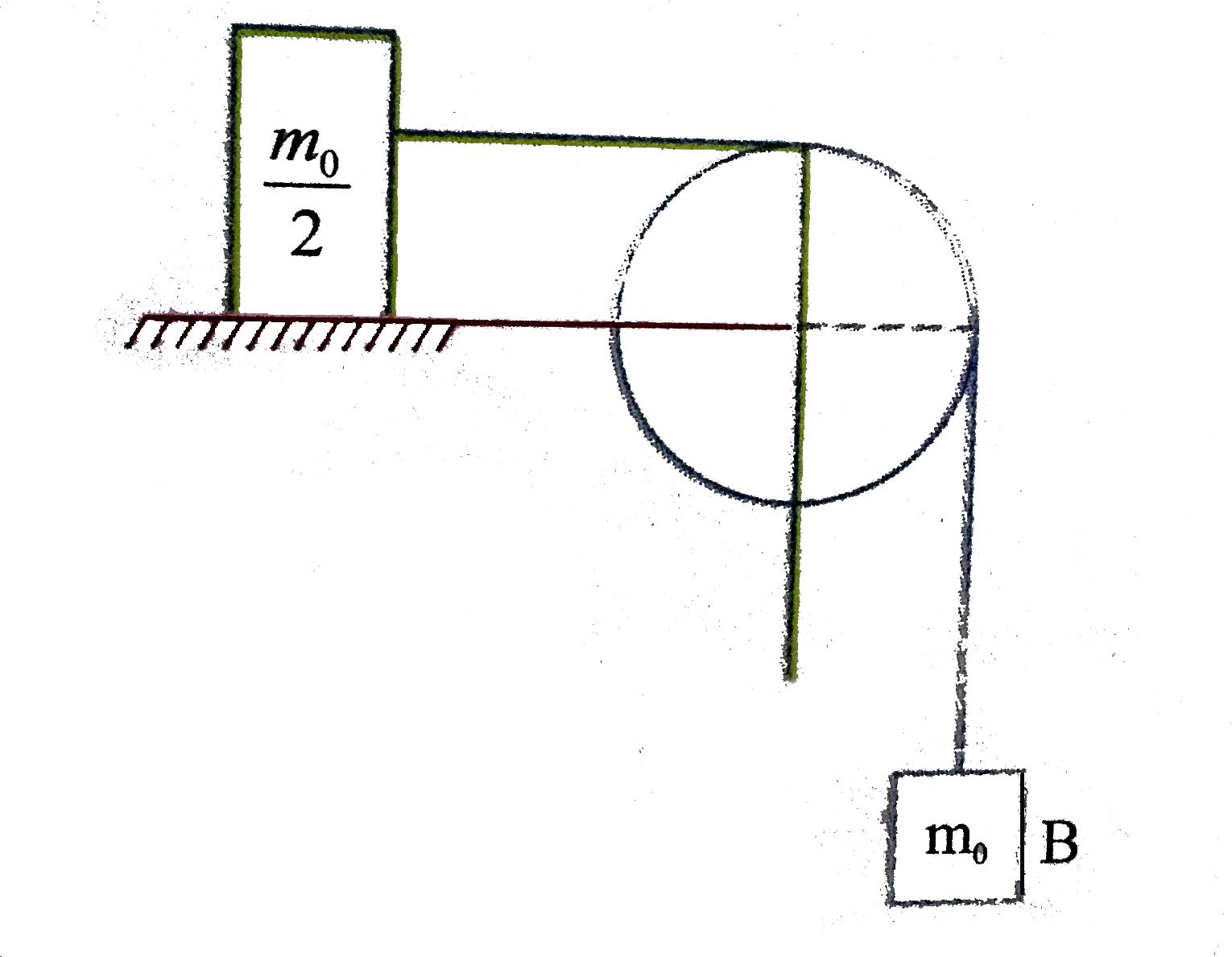
View SolutionIn the arrangement shown in figure what should be the mass of block A, so that the system remains at rest ? Neglect friction and mass of string.

View Solution
Knowledge Check
A block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
AmgBμmgcosθCmgsinθDμmgtanθA solid cylinder is rolling down on an inclined plane of angle θ. The minimum value of the coefficient of friction between the plane and the cylinder to allow pure rolling
A13tanθB23tanθC25tanθD45tanθCoefficient of friction between pulley and light string is μ1. Calculate minimum coefficient of friction between block A and ground such that system can be in equibrium.
 Aμ=2Bμ=2e−μπ2Cμ=eμ1π2Dμ=32
Aμ=2Bμ=2e−μπ2Cμ=eμ1π2Dμ=32
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA solid cylinder of mass m rolls without slipping down an inclined plane making an angle θ with the horizontal. The frictional force between the cylinder and the incline is
View SolutionIn the figure shown a ring of mass M and a block of mass m are in equilibrium. The string is light and pulley P does not offer any friction and coefficient of friction between pole and M is μ. The frictional force offered by the pole to M is

View SolutionIn the pulley arrangement shown in Fig the pulley p2 is movable .Assuming the coefficient of friction between m and surface to be μ the minimum value of M for which m is at rest is

View Solution
