In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
(n+12)λ
nλ
(n−12)λ
λ2
The correct Answer is:B
Constructive interference occurs when the path difference (S1P−S2P) is an integral multiple of λ.
or S1P−S2P=nλ
where n=0,1,2,3,…
Topper's Solved these Questions
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - HIGHER ORDER THINKING SKILLS
8 Videos
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - NCERT EXEMPLAR PROBLEMS
5 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
In Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength 6000Å, coming from the coherent sources S1 and S2. At certain point P on the screen third dark fringe is formed. Then the path difference S1P−S2P in microns is
View SolutionTwo coherent sources S1 and S2 produce interference fringes. If a thin mica plate is introduced in the path of light from S1 then the central maximum
View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View SolutionWhen light from two sources (say slits S1 and S2) interfere, they form alternate dark and bright fringes. Bright fringe is formed at all point where the path difference is an odd multiple of half wavelength. At the condition of equal amplitudes, A1=A2=a, the maximum intensity will be 4a2 and the visibility improves, The resultant intensity can also be indicated with phase factor as I=2a2cos2(ϕ/2).Using this passage, answer the following questions.
If the slits S1 and S2 are arranged as shown in Fig. the ratio of intensity of fringe at P and R is

View SolutionIn the arrangement shown, a screen is placed normal to the line joining the two point coherent sources S1 and S2. The interference pattern consist of concentric circles. λ is the wavelength of light (D>>d).

The phase difference of the interfering light at point P is
View SolutionTwo waves of equal amplitude a from two coherent sources (S1&S2) interfere at a point R such that S2R−S1R=1.5λThe intensity at point R Would be
View SolutionThe wavelength of sound waves arriving at P from two coherent sources S1 and S2 is 4 m as shown. While intensity of each wave is I0 the resultant intensity at point P is 2I0 find minimum value of x
_PHY_E06_238_Q01.png)
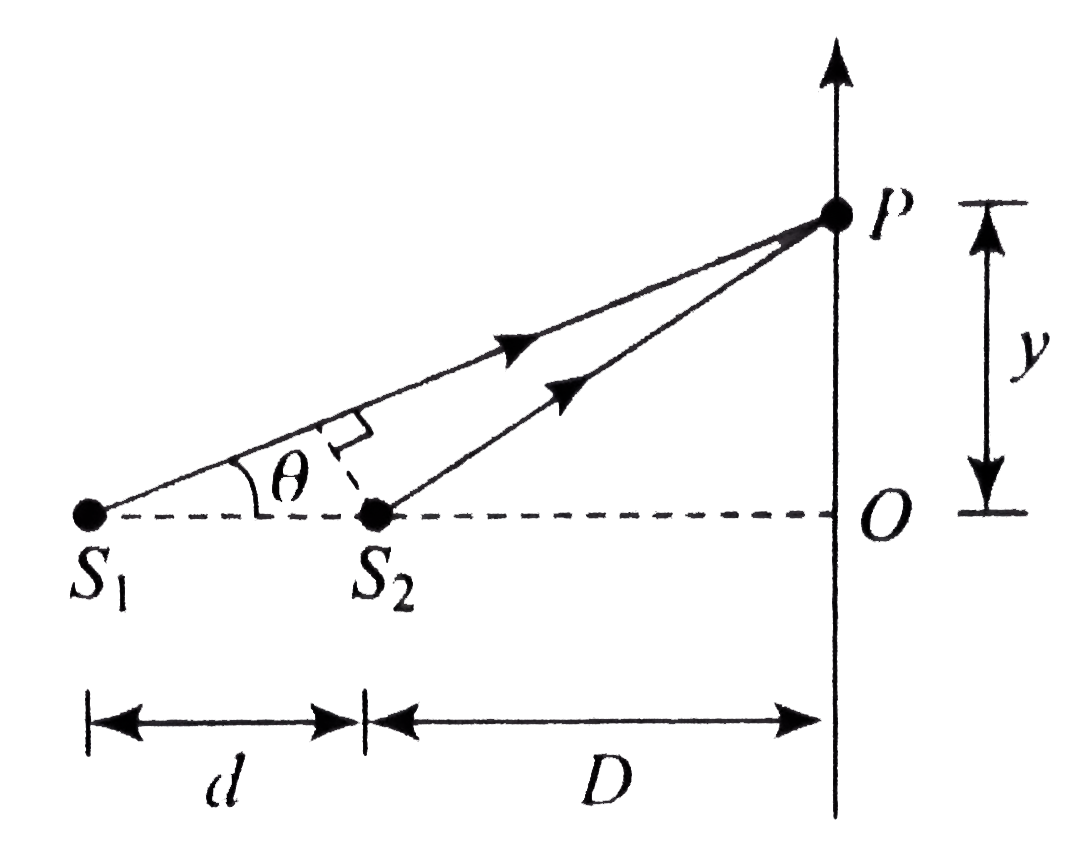
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View SolutionIn figure, a screen is placed normaol to the line joining the two point coherent sources S1 and S2. The interference pattern consists of concentric circles.
Also, find the value of radius for this ring.
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View Solution
