In the figure, pendulum bob on left side is pulled a side to a height h from its initial position. After it is released it collides with the right pendulum bob at rest, which is of the same mass. After the collision the two bobs stick together and raise to a height :-
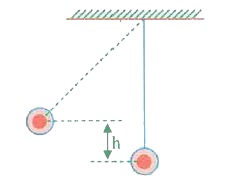
h2
h4
3h3
3h4
The correct Answer is:B
Step by step video & image solution for In the figure, pendulum bob on left side is pulled a side to a height h from its initial position. After it is released it collides with the right pendulum bob at rest, which is of the same mass. After the collision the two bobs stick together and raise to a height :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Linked Comprehension)6videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Problems46videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
The bob of pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. Find the speed v with which the bob passes through the equilibrium position.
View SolutionThe bob A of a pendulum released from a height h hits head-on another bob B of the same mass of an identical pendulum initially at rest. What is the result of this collision? Assume the collisio to be elastic (see figure).
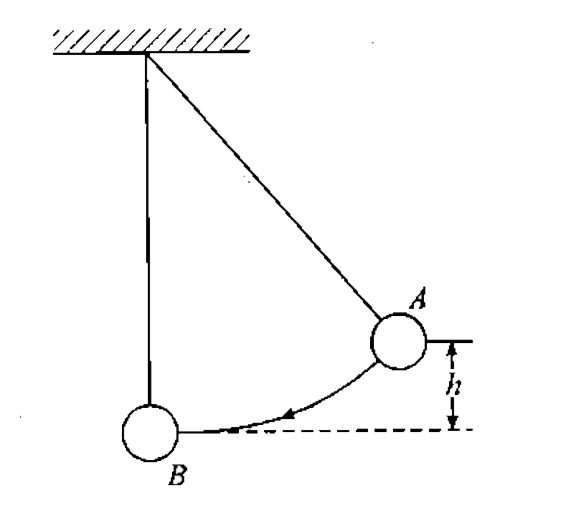 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
A√2g1−sinθB√2g1+cosθC√2g1−cosθD√2g1+sinθ - Question 2 - Select One
The bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
A√2g1−sinθB√2g1+cosθC√2g1−cosθD√2g1+sinθ - Question 3 - Select One
Two pendulum bobs of mass m and 2m collide elastically at the lowest point in their motion. If both the balls are releasd from height H above the lowest point,
Velocity of the bob of mass m just after collision isA√2gH3B53√2gHC√2gHDNone of these
The bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals
View SolutionIn an arrangement shown , bob A on the left is pulled aside . It is then released and allowed to collide with other bob B which is at rest . A perfectly inelastic collision occurs and the system rises to a height h/4 . The ratio of the masses of the bobs is
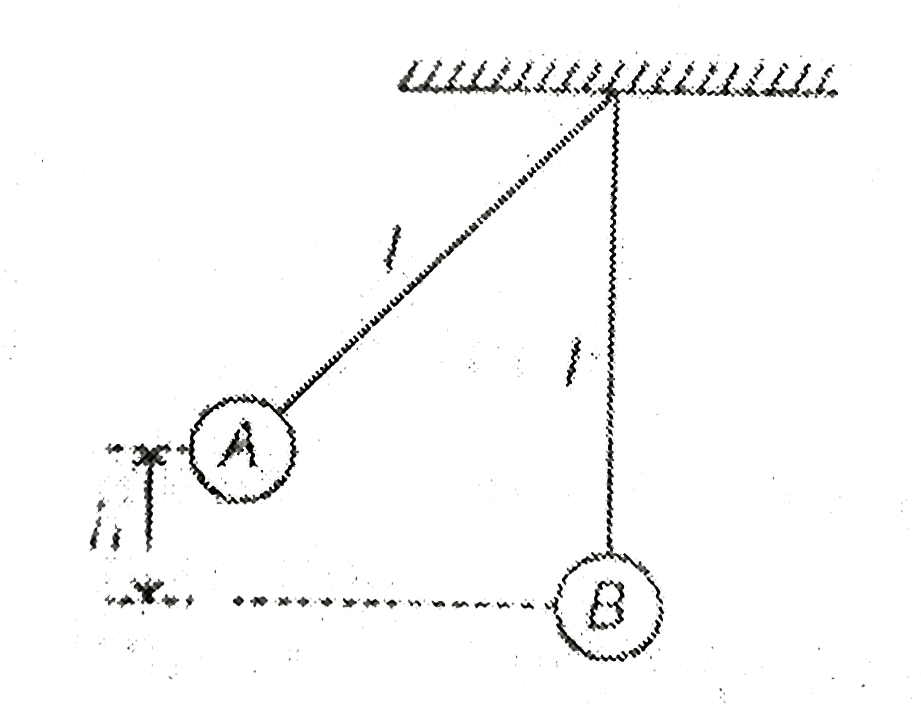 View Solution
View SolutionTwo pendulum bobs of masses m and 2m collide head on elastically at the lowest point in their motion. If both the balls are released from a height H above the lowest point, to what heights do they rise for the first time after collision?
View SolutionThe bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals
View SolutionA simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View Solution

