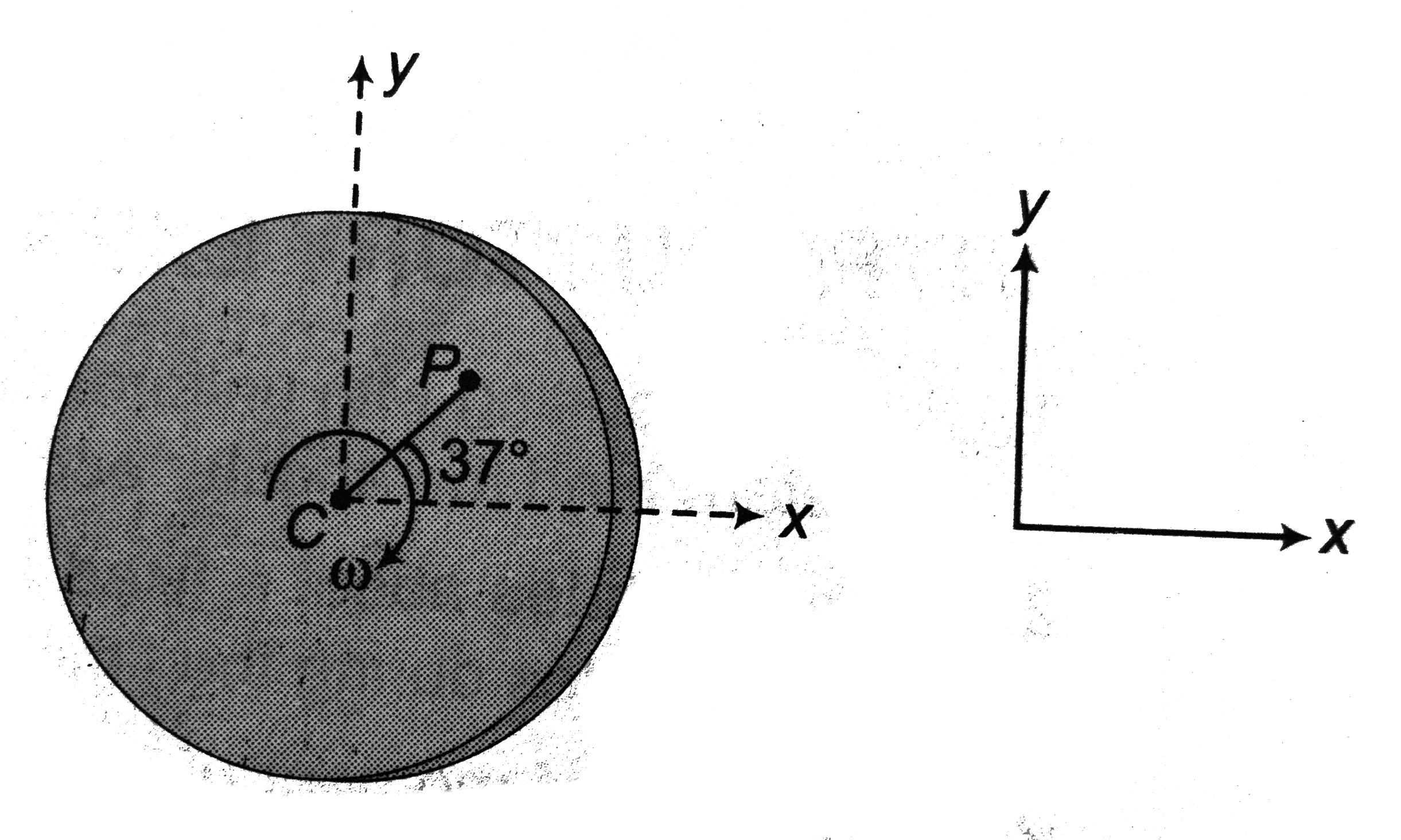
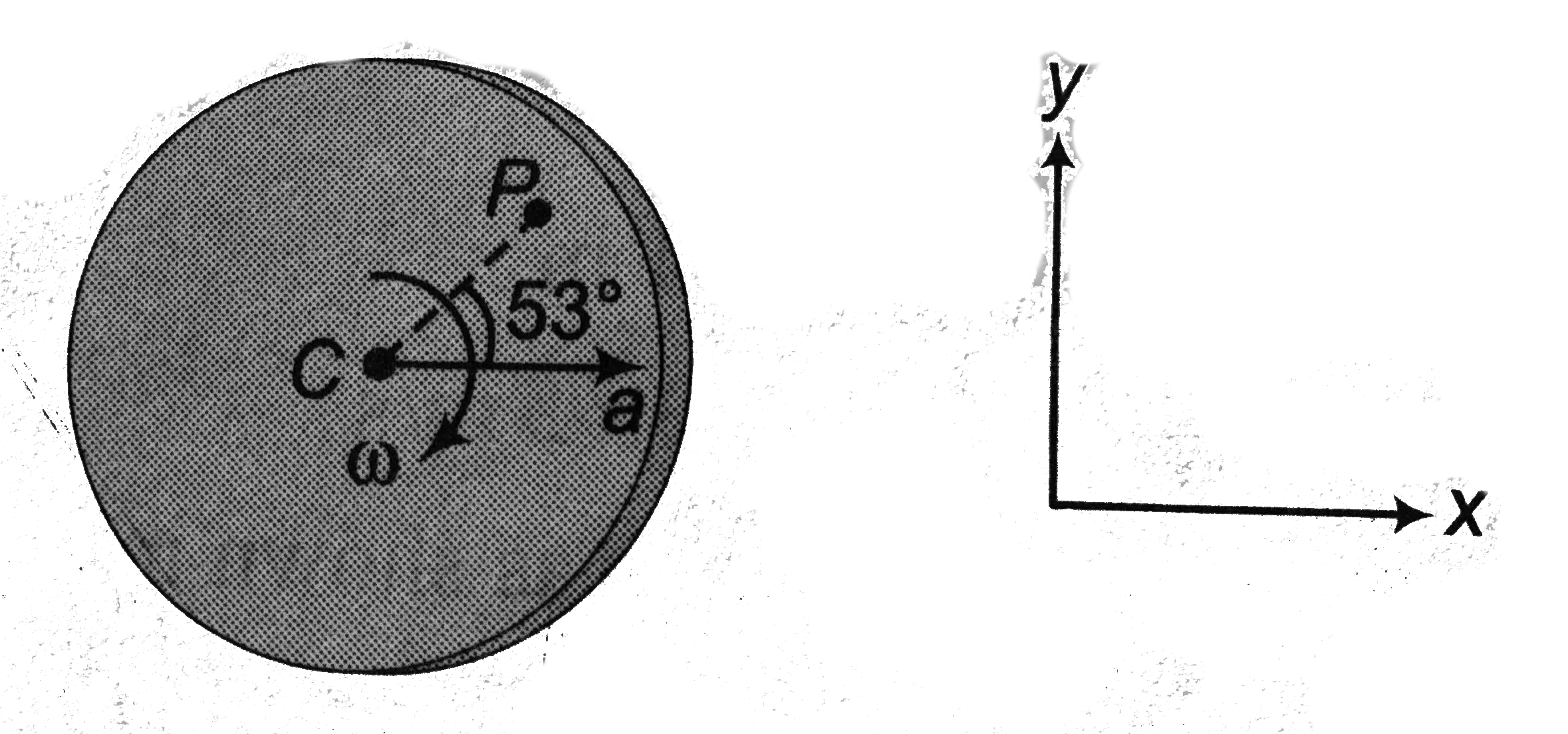In the figure shown υ=2m/s ω=5rad/s and CP=1m
In terms of ˆi and ˆj find linear velocity of particle P.
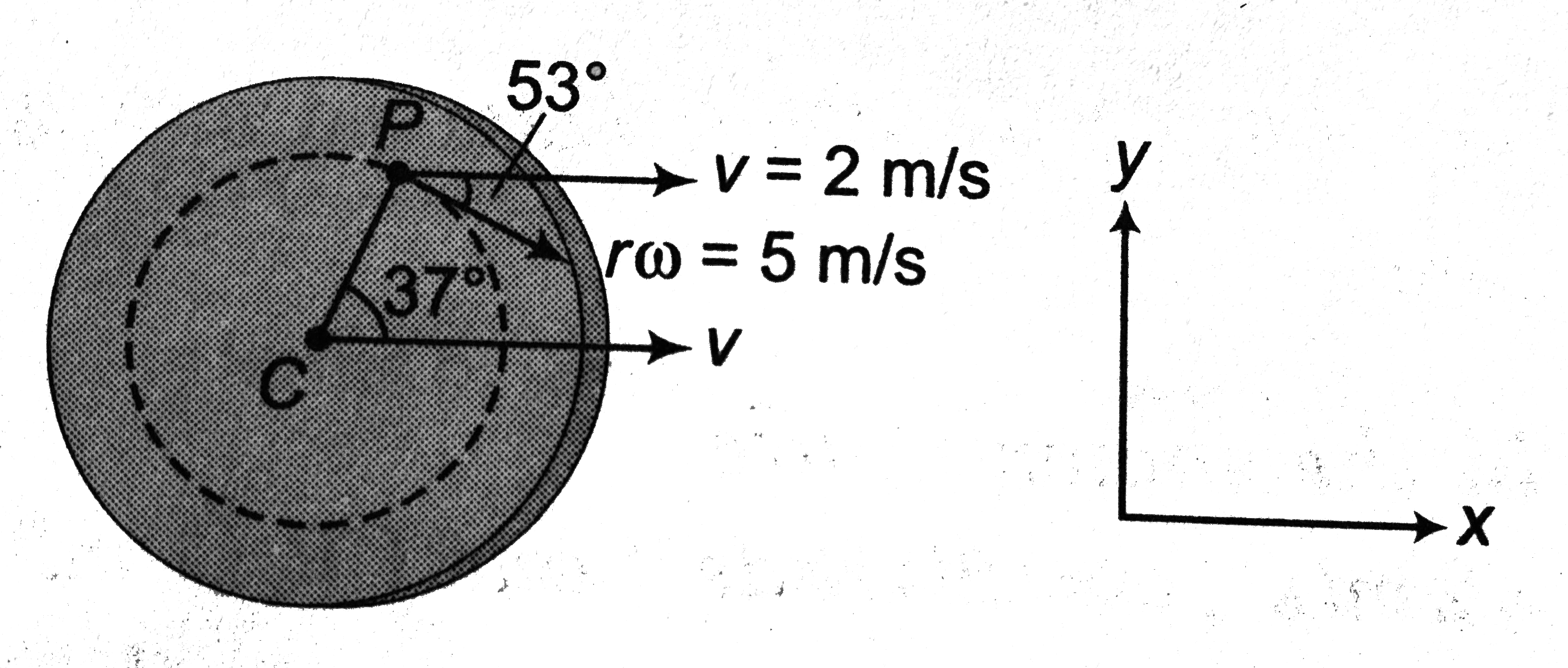
For particle P,
r=CP=1m
⇒rω=(1)(5)=5m/s
Net velocity of P is the vector sum of v and rω as shown in figure.
∴VP=2ˆi+(5cos53∘ˆi−5sin53ˆj)
=2ˆi+3ˆi−4ˆj=(5ˆi−4ˆj)m/s
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples
25 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Knowledge Check
In the figure the variations of componets of acceleration of particles of mass 1kg is shown w.r.t. time. The initial velocity of the particle is →u=(−3ˆi+4ˆj)m/s. the total work done by the resultant force on the particles in time intervals from t=0 to t=4 seconds is :
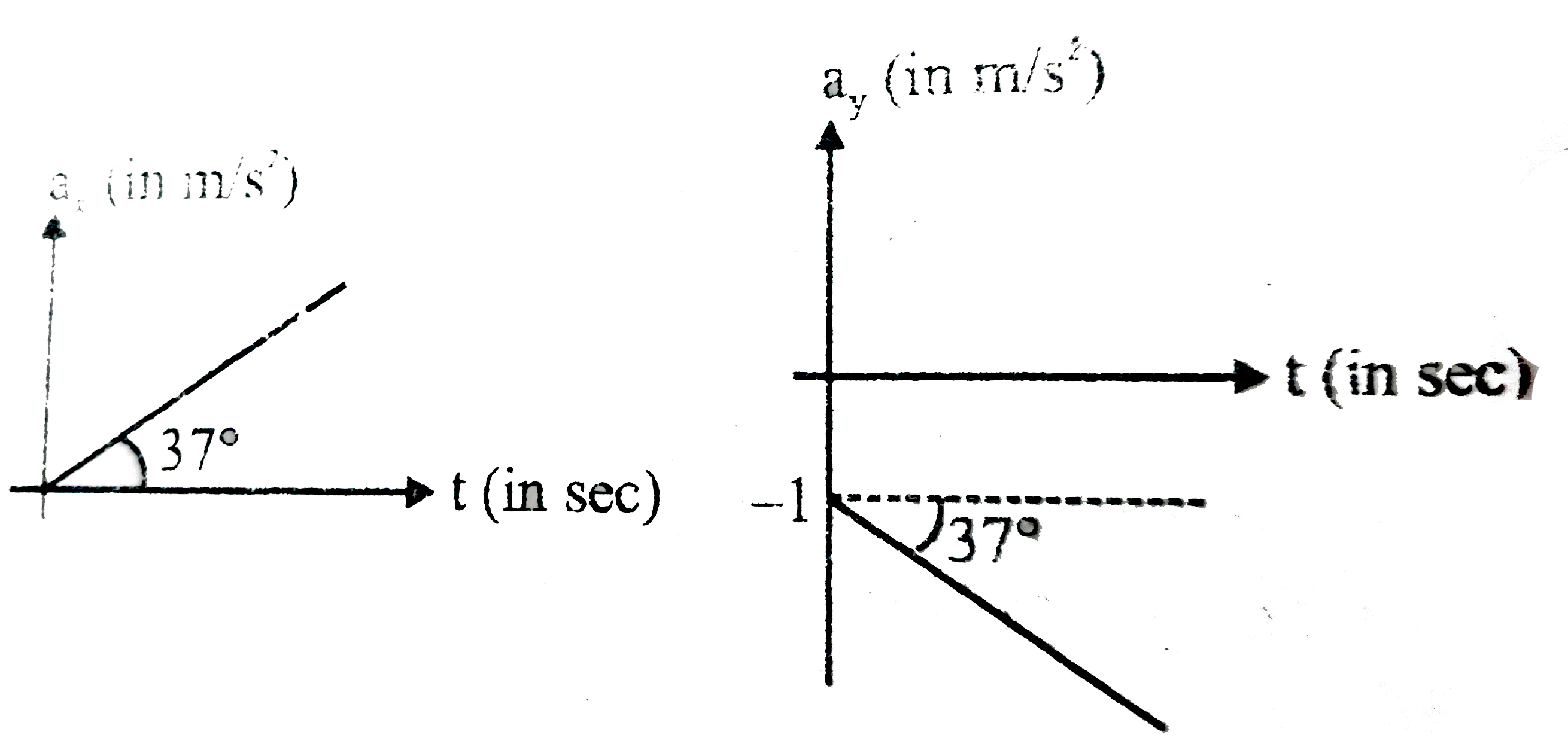 A22.5JB10 JC0DNone of these
A22.5JB10 JC0DNone of theseA particle is moving with uniform speed 0.5m/s along a circle of radius 1m then the angular velocity of particle is (in rads−1)
A2B1.5C1D0.5
A circular disc is rotating with an angular speed (in radian per sec)
ω=2t2
given, CP=2m
In terms of ˆi,ˆj and ˆk at t=1s
find,
(a). ω
(b). α
(c). linear velocity of the particle lying at P (d). linear acceleration of the particle lying P
View SolutionIf angular velocity of a particle having position vector →r=(2ˆi−2ˆj+2ˆk)m about the origin is →w=(2ˆi−2ˆj−ˆk)rads then magnitude of linear velocity of the particle will be
View SolutionIf angular velocity of a point object is →ω=(ˆi+ˆ2j−ˆk) rad/s and its position vector →r=(ˆi+ˆj−5ˆk)m then linear velocity of the object will be
View SolutionThe acceleration of a particle is given by the relation as a=−kv5/2 , where is a constant. The particle starts at x=0 with a velocity of 16 m/s, and when x = 6, the velocity is observed to be 4 m/s. Find the velocity of particle when x=5m and the time at which the velocity ofthe particle is 9 m/s.
View SolutionA particle is moving in x-y plane. Its initial velocity and acceleration are u=(4ˆi+8ˆj)m/sanda=(2ˆi−4ˆj)m/s2. Find
(a) the time when the particle will cross the x-axis.
(b) x-coordinate of particle at this instant.
(c) velocity of the particle at this instant.
Initial coordinates of particle are (4m,10m).
View SolutionA particle describing circular motion as shown in figure. The velocity of particle in m s is-
View Solution