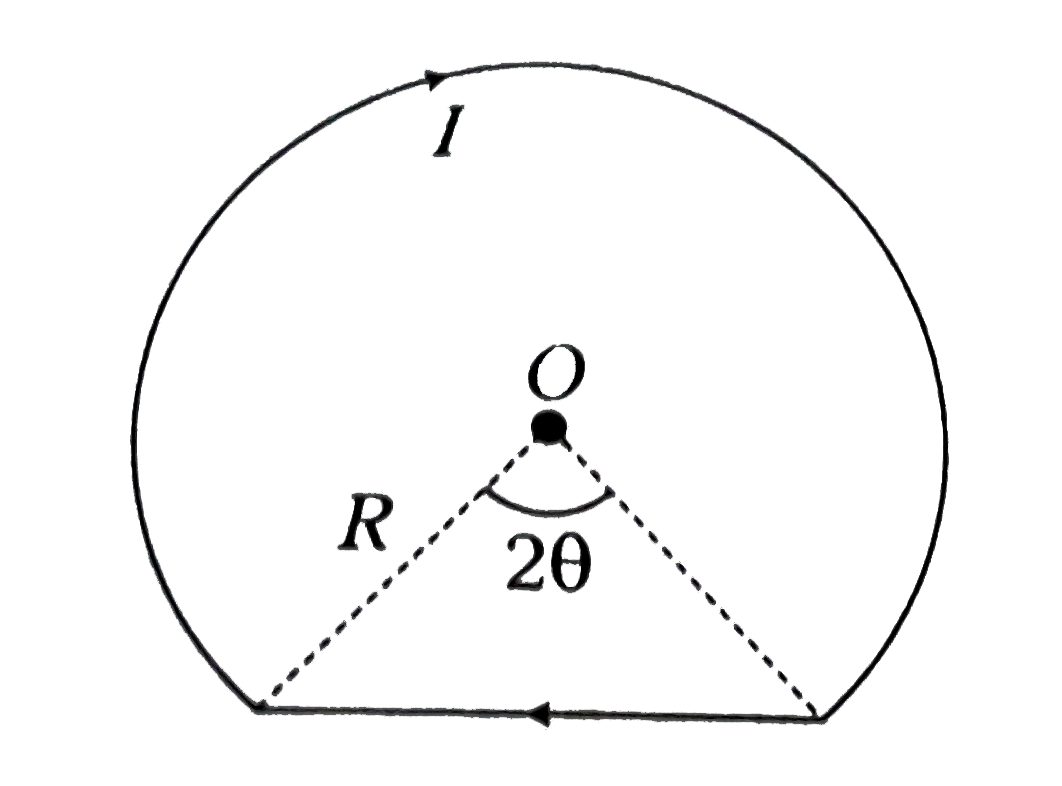
In the following figure a current loop is shown which is made from two circular arcs of radii a and b(a<b), connected by radial wires. Calculate the magnetic field at the centre O.

μ0iθ4πab(b−a), inwards
μ0iθ4πab(b−a), outwards
μ0iθ3πab(b−a), inwards
Zero
The correct Answer is:B
Wires that are connected radially produce no magnetic field at the centre as these are passing through the centre when extended backwards. Only circular arcs are producing magnetic field at the centre. The inner coil produces an outward magnetic field but the outer coil produces an inward magnetic field, hence the resultant will be the difference of the two. The outward field of the inner coil will be more than that, due to the outer arc, and hence the net magnetic field will be directed outward.
B=θ2π[μ0i2a−μ0i2b]=μ0iθ4πab(b−a)
Thus, option (b) is correct.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)79videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)28videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Numerical Problems )18videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
A cube made from wires of equal length is connected to a battery as shown in the figure. The magnetic field at the centre of the cube is
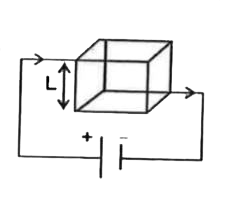 A12μ0l√2πLB6μ0I√2μLC6μ0lπLDzero
A12μ0l√2πLB6μ0I√2μLC6μ0lπLDzero - Question 2 - Select One
A cube made of wire of equal length is connected to a battery as shown in figure.The magnetic field at the centre of the cube is
 A12√2μ0IπLB6μ0I√2πLC6μ0IπLDzero
A12√2μ0IπLB6μ0I√2πLC6μ0IπLDzero - Question 3 - Select One
A cube made of wires of equal length is connected to a battery as shown in the figure. The magnetic field at the centre of the cube is
 A12μ0I√2πLB6μ0I√2πLC6μ0I√2πLDzero
A12μ0I√2πLB6μ0I√2πLC6μ0I√2πLDzero
A wire loop formed by joining two semicircular wires of radii R1 and R2 carries a current I as shown in figure. Find the magnetic field induction at the centre O.
 View Solution
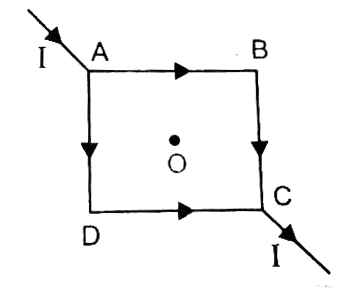
View SolutionFigure shows a square loop made from a uniform wire. If a battery is connected between the pionts A and C. What will be the magnetic field at the centre O of the square?
 View Solution
View SolutionA straight wire carrying a current of 12 A is bent into a semi-circular are of radius of2.0 cm as shown in the adjoining figure (a). Consider the magnetic field B at the centre of the arc. Would your answer be different if the wire were bent into a semi-circular arc of the same radius but in the opposite way a shown in figure (b)?
 View Solution
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA current I flows through a closed loop as shown in figure .The magnetic field at the centre O is
 View Solution
View Solution


