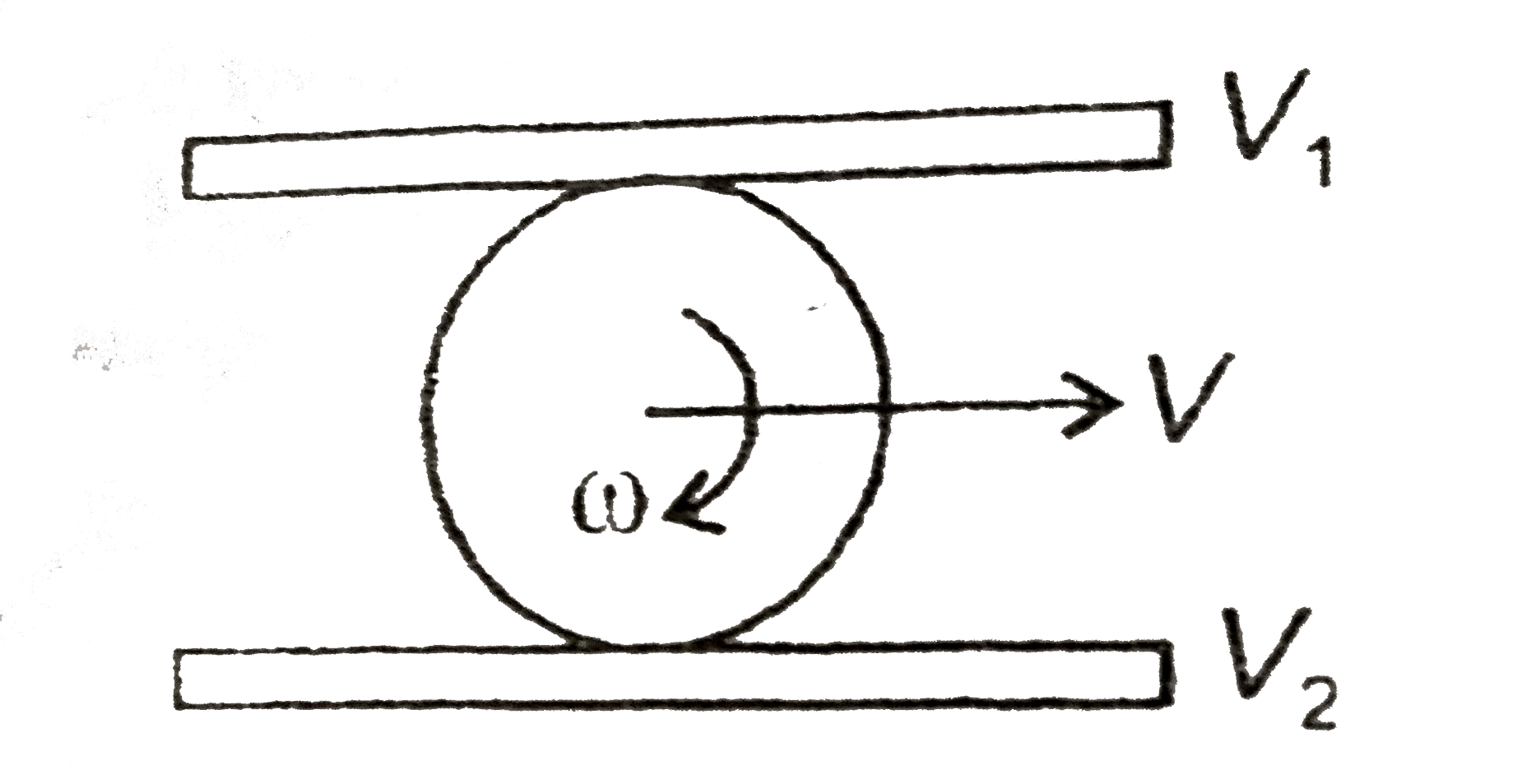
In the given figure, the spheres rolls without slipping on the plank which is moving with constant velocity v0. The radius and angualr velocity of the sphere is r and ω, respectively. The velocity of center fo mass of the sphere is

v0+rω
V0−rω
rω
v0
a) For pure rolling motion of sphere, relative motioin of point of contact of sphere and plank should be zero. For this, the point of contact has a velocity equal to the velocity of plank.
∴ v0=vCM−rω
∴ vCM=v0+rω
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - BITSAT GUIDECHAPTER - ROTATIONAL MOTIONEXERCISE - BITSAT Archives
9 Videos
- NEWTONS LAWS OF MOTION AND FRICTIONBOOK - BITSAT GUIDECHAPTER - NEWTONS LAWS OF MOTION AND FRICTIONEXERCISE - BITSAT Archives
23 Videos
- SCALARS AND VECTORSBOOK - BITSAT GUIDECHAPTER - SCALARS AND VECTORSEXERCISE - All Questions
34 Videos
Similar Questions
A sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
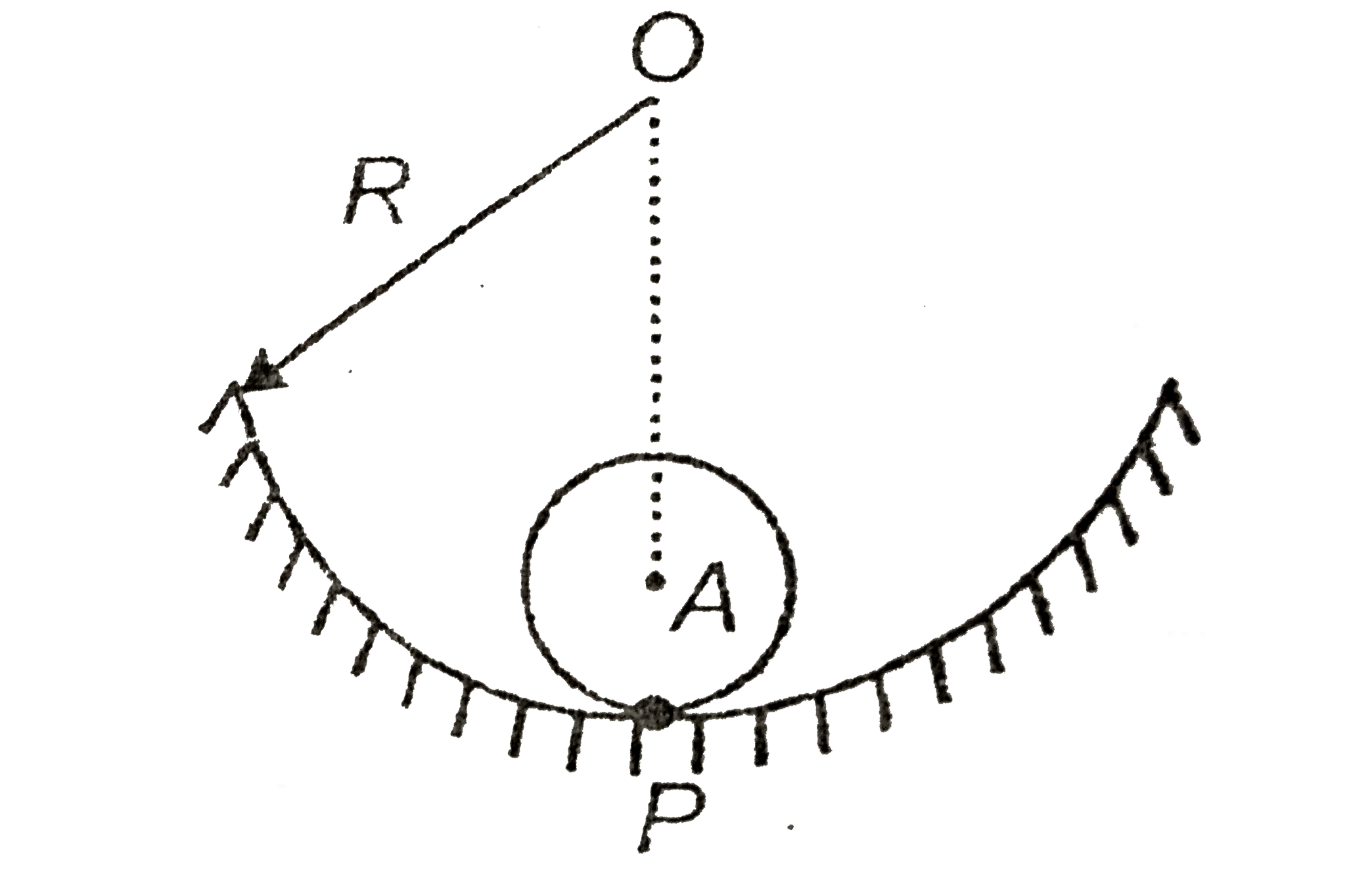
View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
View Solution
Knowledge Check
A sphere of mass m moving with a constant velocity u hits another stationary sphere of the same mass and of coefficient of restitution (e). The ratio of velocities of the two spheres, after collision, will be
Ae(e+1)B(1−e1+e)C1eD(e+1e)A sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
A45Mv0R(−ˆk)B95Mv0R(−ˆk)C85Mv0R(−ˆk)D75Mv0R(−ˆk)A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
A0.014 JB0.028 JC14 JD28 J
A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionA solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
View Solution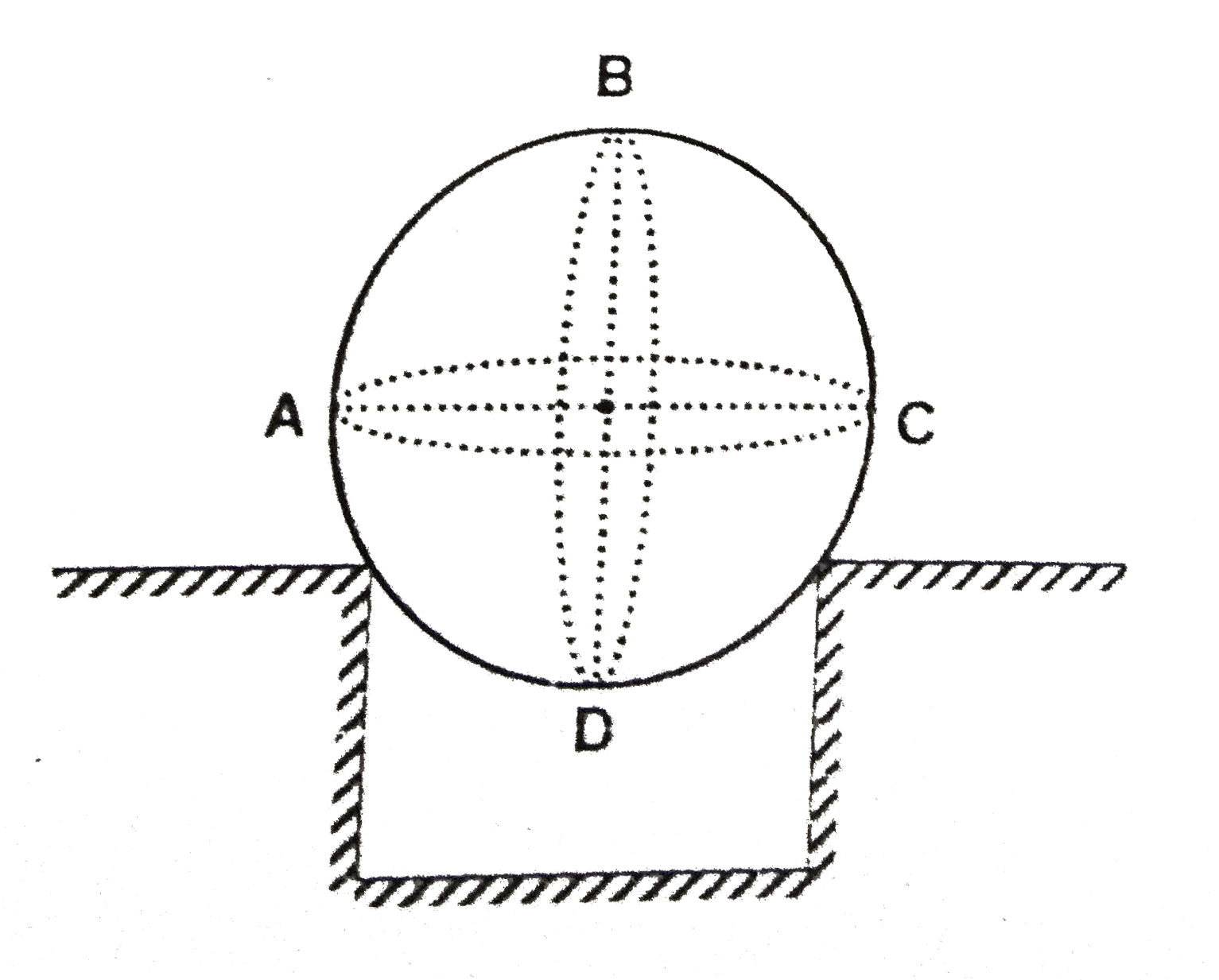
A sphere of mass m and radius r rolls without slipping over a tunnel of width d=8r5 as shown in the figure. (in the figure the sphere rolls perpendicular to the plane of the page) the velocity of centre of mass of sphere is v directed into the plane of the page. the maximum speed of a point on the sphere is
View SolutionA solid sphere with a velocity (of centre of mass) v and angular velocity ω is gently placed on a rough horizontal surface. The frictional force on the sphere :
View SolutionA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
View Solution
