In the one-dimensional motion of a particle, the relation between position x and time t is given by x2+2x=t (here x>0). Choose the correct statement
the retardatioin of the particle is 14(x+1)3
the uniform velocity of the particle is 1(x+1)3
Both are correct
Both are wrong
The correct Answer is:A
To solve the problem, we need to analyze the given equation relating position x and time t:
x2+2x=t
Step 1: Differentiate the equation with respect to time t
We start by differentiating both sides of the equation with respect to t:
ddt(x2+2x)=ddt(t)
Using the chain rule on the left side:
2xdxdt+2dxdt=1
Step 2: Factor out dxdt
Now, we can factor out dxdt:
dxdt(2x+2)=1
Step 3: Solve for velocity v
Now, we can express the velocity v=dxdt:
v=12x+2
Step 4: Find acceleration a
To find acceleration, we need to differentiate the velocity with respect to time. We can use the chain rule again:
a=dvdt=dvdx⋅dxdt
First, we need to find dvdx:
v=(2x+2)−1
Using the power rule and chain rule:
dvdx=−1⋅(2x+2)−2⋅2=−2(2x+2)2
Now substituting dxdt=v:
a=dvdx⋅v=−2(2x+2)2⋅1(2x+2)=−2(2x+2)3
Step 5: Express retardation
Since retardation is the negative acceleration, we take the negative of a:
Retardation=2(2x+2)3
Conclusion
The correct statement regarding the motion of the particle is that the retardation is given by:
Retardation=14(x+1)3
Thus, the first statement is correct.
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
The position of a particle moving in the xy plane at any time t is given by x=(3t2−6t) metres, y=(t2−2t) metres. Select the correct statement about the moving particle from the following
View SolutionThe position of a particle moving in the xy plane at any time t is given by x=(3t2−6t) metres, y=(t2−2t) metres. Select the correct statement about the moving particle from the following
View Solution
Knowledge Check
For the one dimensional motion, described by x=t−sint
Ax(t)>0 for all t gt 0Bν(t)>0 for all t>0Ca(t)>0 for all t>0Dall of these
A particle moves in a straight line and its position x at time t is given by x2=2+t. Its acceleration is given by :-
View SolutionThe displacement x of a particle moving along x-axis at time t is given by x2=2t2+6t. The velocity at any time t is
View SolutionThe displacement of a particle moving in a straight line depends on time as x=αt3+βt2+γt+δ. The ratio of initial acceleration to its initial velocity depends
View SolutionRelation between displacement x and time t is x=2−5t+6t2, the initial acceleration will be :-
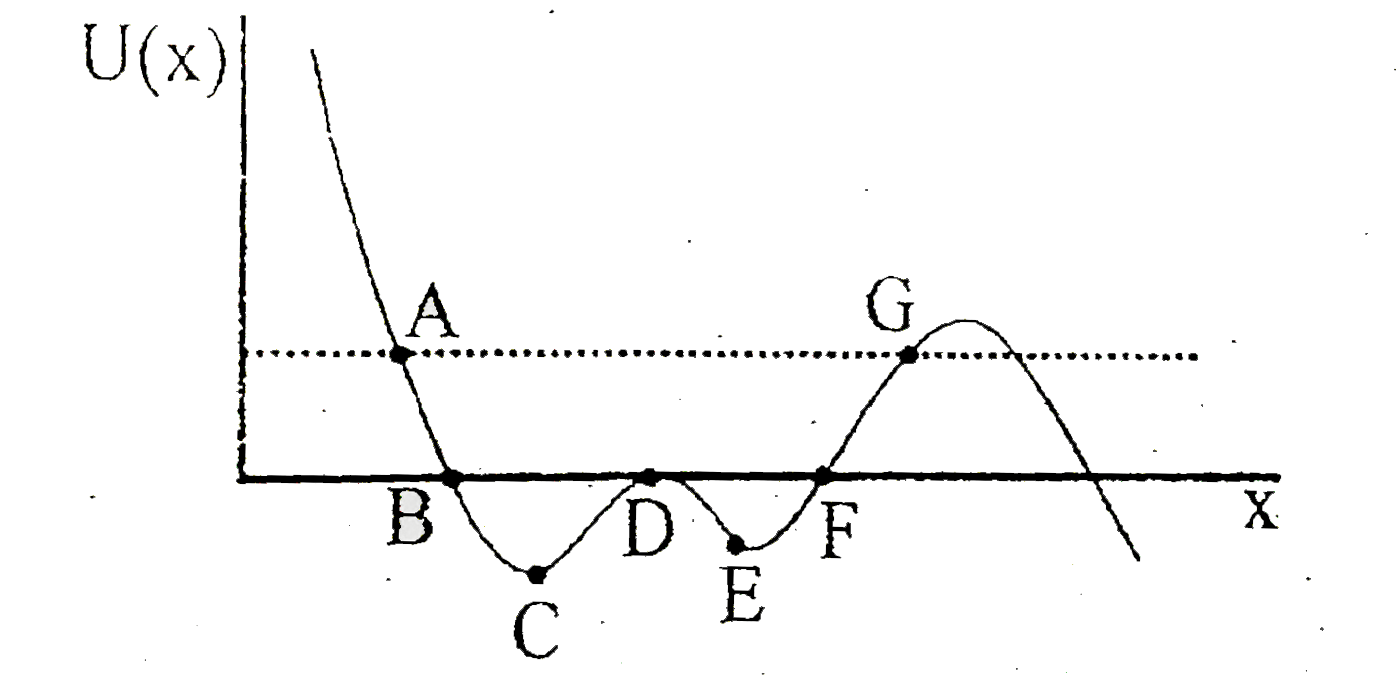
View SolutionThe figure below shows a graph of potential energy U(s) verses position x for a particle executing on edimensional motion along the x axis. The total mechanical energy of the system is indicated by the dashed line. At t=0 the particle is somewhere between points A and G. For later times choose the correct statement:-
View SolutionThe position x of a particle with respect to time t along the x-axis is given by x=9t2−t3 where x is in meter and t in second. What will be the position of this particle when it achieves maximum speed along the positive x direction
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View Solution
