In the pulley system shown the movable pulleys A,B and C have mass m each, D and E are fixed pulleys. The strings are vertical light and inextensible Then
 .
.
Constraint relations,
Let y1,y2andy3 are the positions of pulleys A, B and C respectively at any instant with respect to a dotted line shown in The total length of string
2y1+y2+(y2−y1)+y3+(y3−y2)+l0=l
or y1+y2+2y3+l0=l ...(i)
Where l0 is the length of part of string over the pulleys, which is constant
Differentiating equation (i) w.r.t. time, we get
dy1dt+dy2dt+2dy3dt=0

or v1+v2+2v3=0 ...(ii)
also a1+a2+2a3=0
Let a1=a upward
and a2=a upward
then a=(a1+a22)=a downward
Since string is same throughout and uniform the tension in it will be same every where, thus
From pulley A,
2T−(T+1g)=1a, ...(i)
Form pulley B,
2T−(T+1g)=1a ...(ii)
From pulley C,
1g−2T=1a ...(iii)
Solving above equations , we get
a1=−g3,a2=−g3,a3=g3
and T=2g3=6.53N
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Objective Questions
134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
Knowledge Check
In the pulley system shown in fifure the movable pullet=ys A,B and C are of mass 1 kg each D and E are fixed pulleys are light and inexensible.
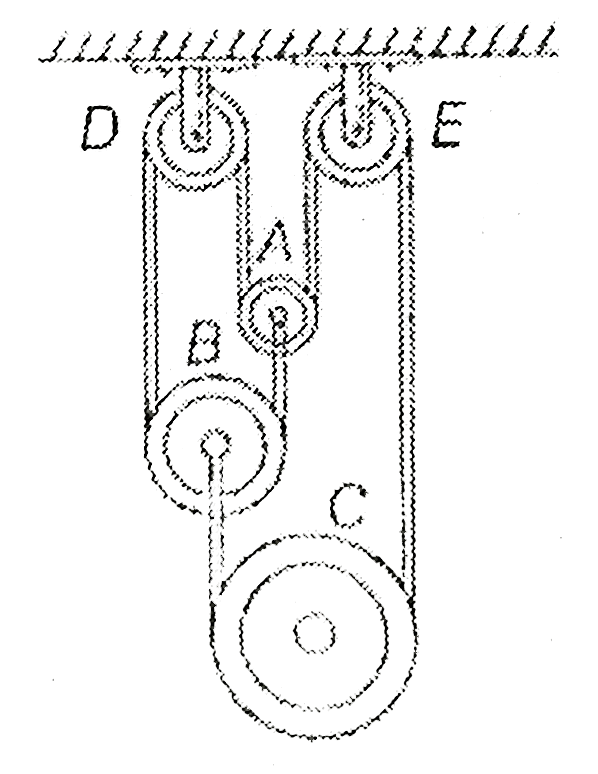
Choose the correct alternative (s).ATension in the string is 6.5 NBAcceleration of pulley A is g/3 downwardCAcceleration of pulley B is g.\6 upwardDAcceleration of pulley C is g/3 upwardAssume that all the pulleys are massless and frictionless and strings to be inextensible.
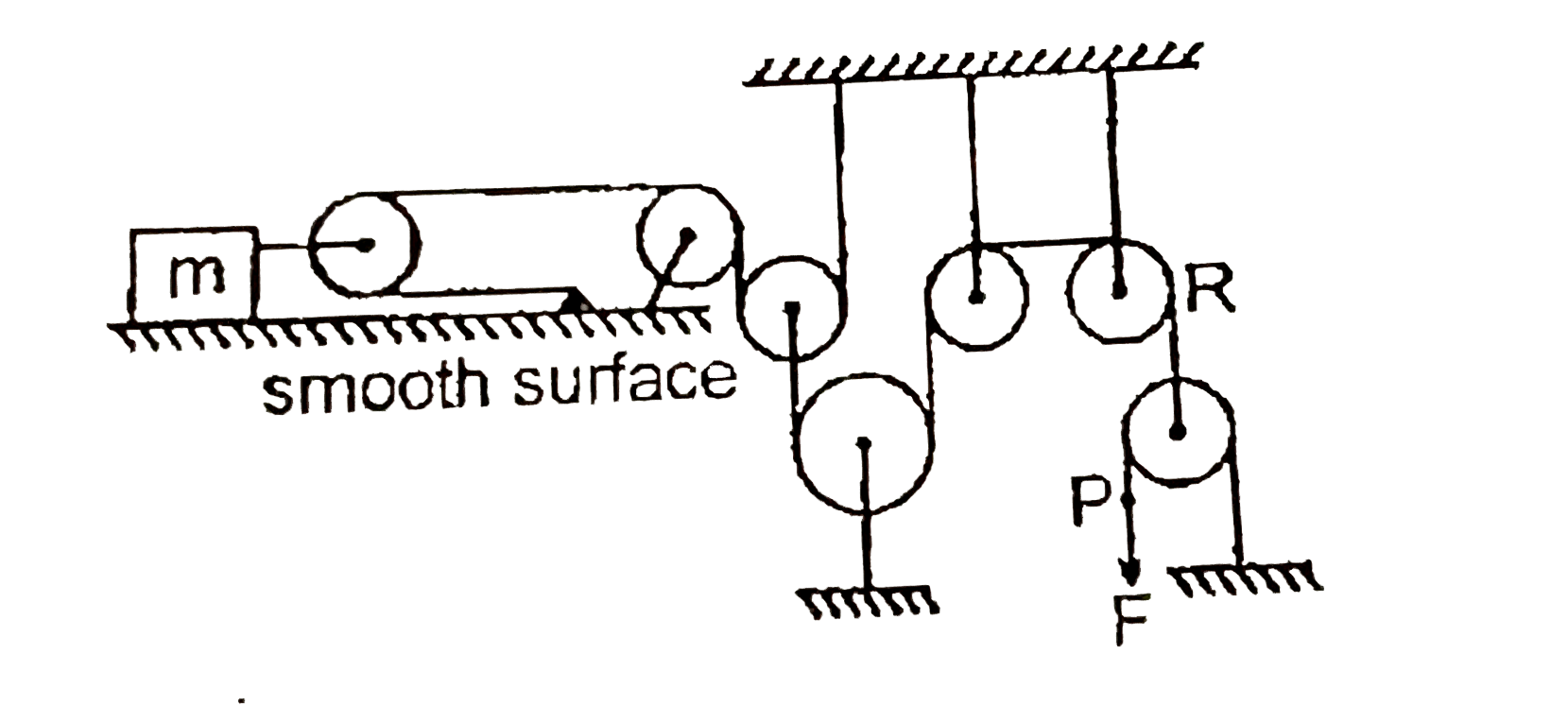 AAcceleration of P is 4 F/mBAcceleration of m is F/mCAcceleration of P is 2F/mDAcceleration of m is F/2m
AAcceleration of P is 4 F/mBAcceleration of m is F/mCAcceleration of P is 2F/mDAcceleration of m is F/2mIn the system shown in fig the pulley is frictionless and the string massless if m1=m2 thrust on the pulley will be:
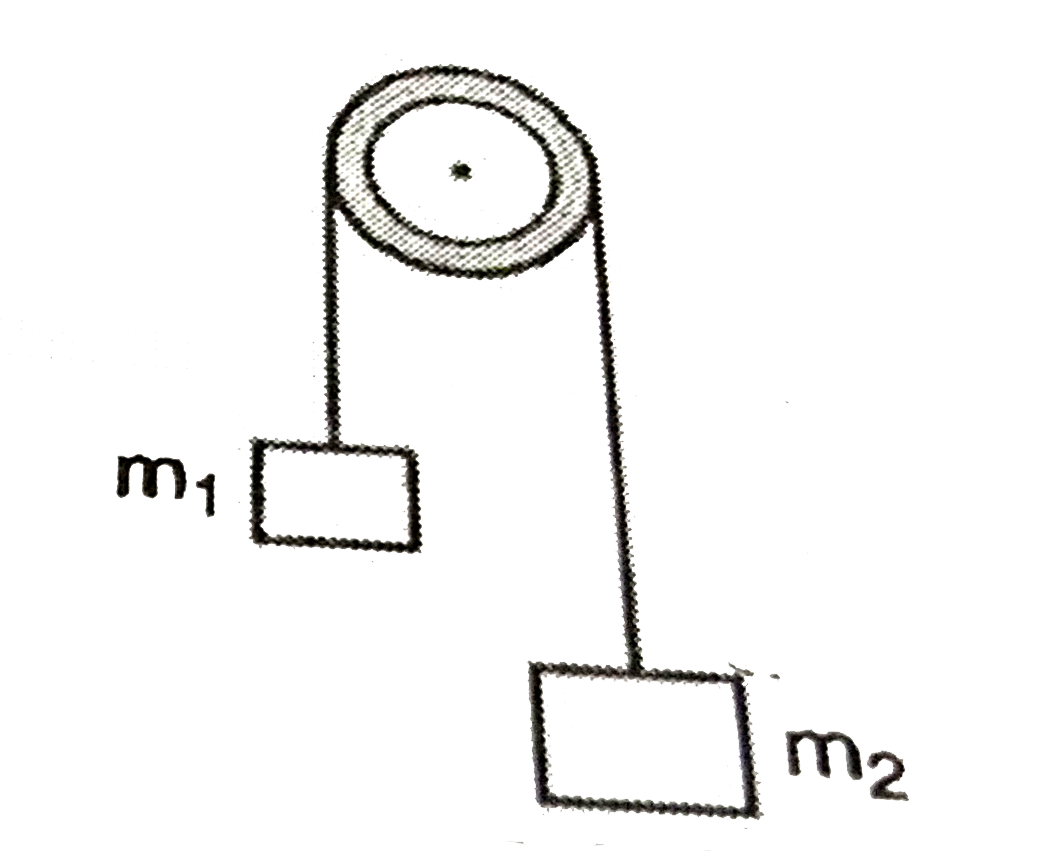 Aless than(m1+m2)gBgreater than(m1+m2)gCequal to (m1+m2)gDnone of the above
Aless than(m1+m2)gBgreater than(m1+m2)gCequal to (m1+m2)gDnone of the above
Find the acceleration of two masses as shown in figure . The pulley are light and frictionless and string are light and frictionless and string are light and inextensible.

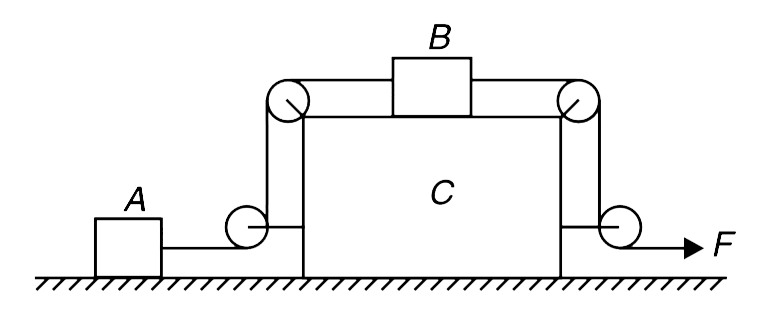
View SolutionIn the system shown in the figure, all surfaces are smooth. Block A and B have mass m each and mass of block C is 2 m. All pulleys are massless and fixed to block C. Strings are light and the force F applied at the free end of the string is horizontal. Find the acceleration of all three blocks.
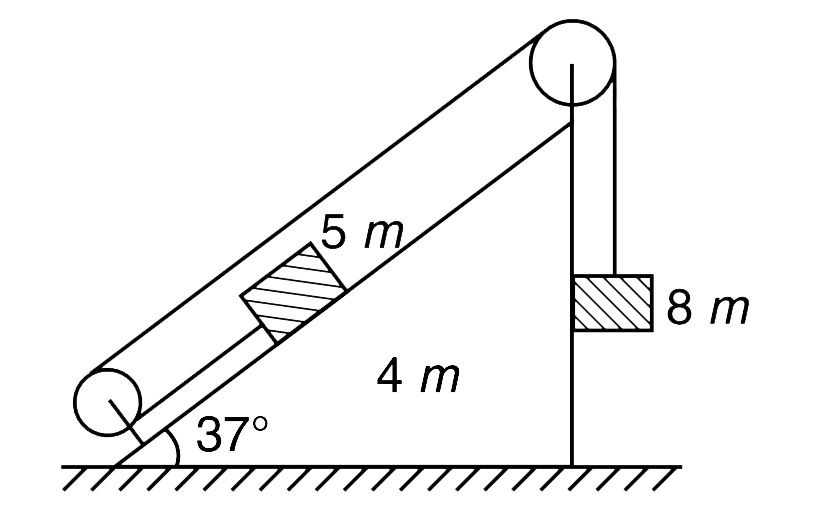
View SolutionIn the system shown in the figure all surfaces are smooth, pulley and string are massless. The string between the two pulleys and between pulley and block of mass 5 m is parallel to the incline surface of the block of mass 4 m. The system is released from rest. Find the acceleration of the block of mass 4 m . [tan37∘=34]
View SolutionIn the system shown in the given figure, the inline is frictionless, the string is massless, and inextensible pulley is light and frictionless. The system is released from rest.

View SolutionAn arrangement of the masses and pulleys is shown in the figure. Strings connecting masses A and B with pulley are horizontal and all pulleys and strings are light. Friction coefficient between the surface and the block B is 0.2 and between block A and B is 0.7. The system is released from rest. (use g=10m/s2)
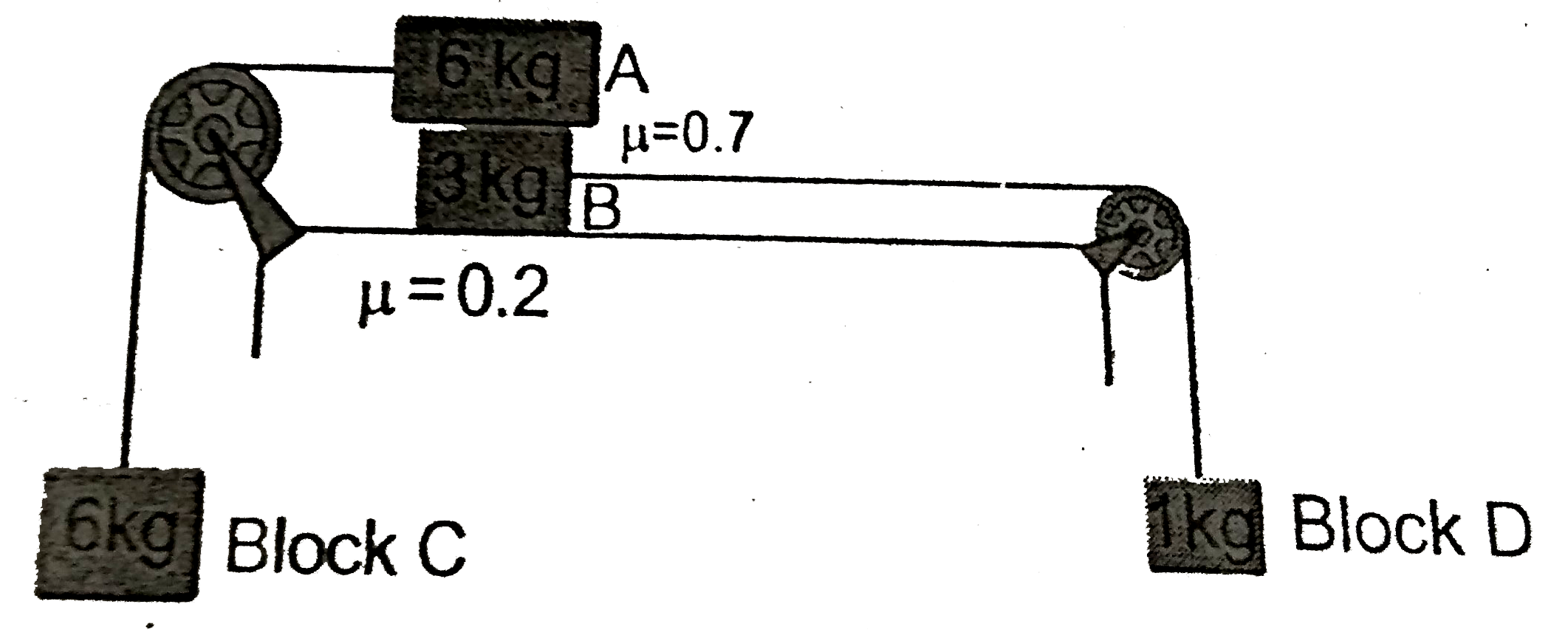
View Solution
