In the two block spring system, force constant of spring is k = 6N/m. Spring is stretched by 12 cm and then left. Match the following.

The correct Answer is:(A→q,B→s,C→p)
ω=√kμ
Here, μ=reduced mass
=m1m2m1+m2=23kg
∴ω=√62/3=3rads−1
Amplitude 12 cm distance in inverse ratio of mass,
∴A1=8cm and A2=4cm
Now, maximum kinetic energy
K1=12m1ωA21
=12×1×3×(8×10−2)2=9.6mJ
K2=12×2×3×(4×10−2)2=4.8mJ
Similar Questions
Force constant of a spring (k) is anonymous to
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionIn spring-block system match the following

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionA long spring is stretched by 3 cm and its potential energy is V . If the spring is stretched by 6 cm ,its potential energy will be
View SolutionComparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
View SolutionIn a spring-block system, match the following:
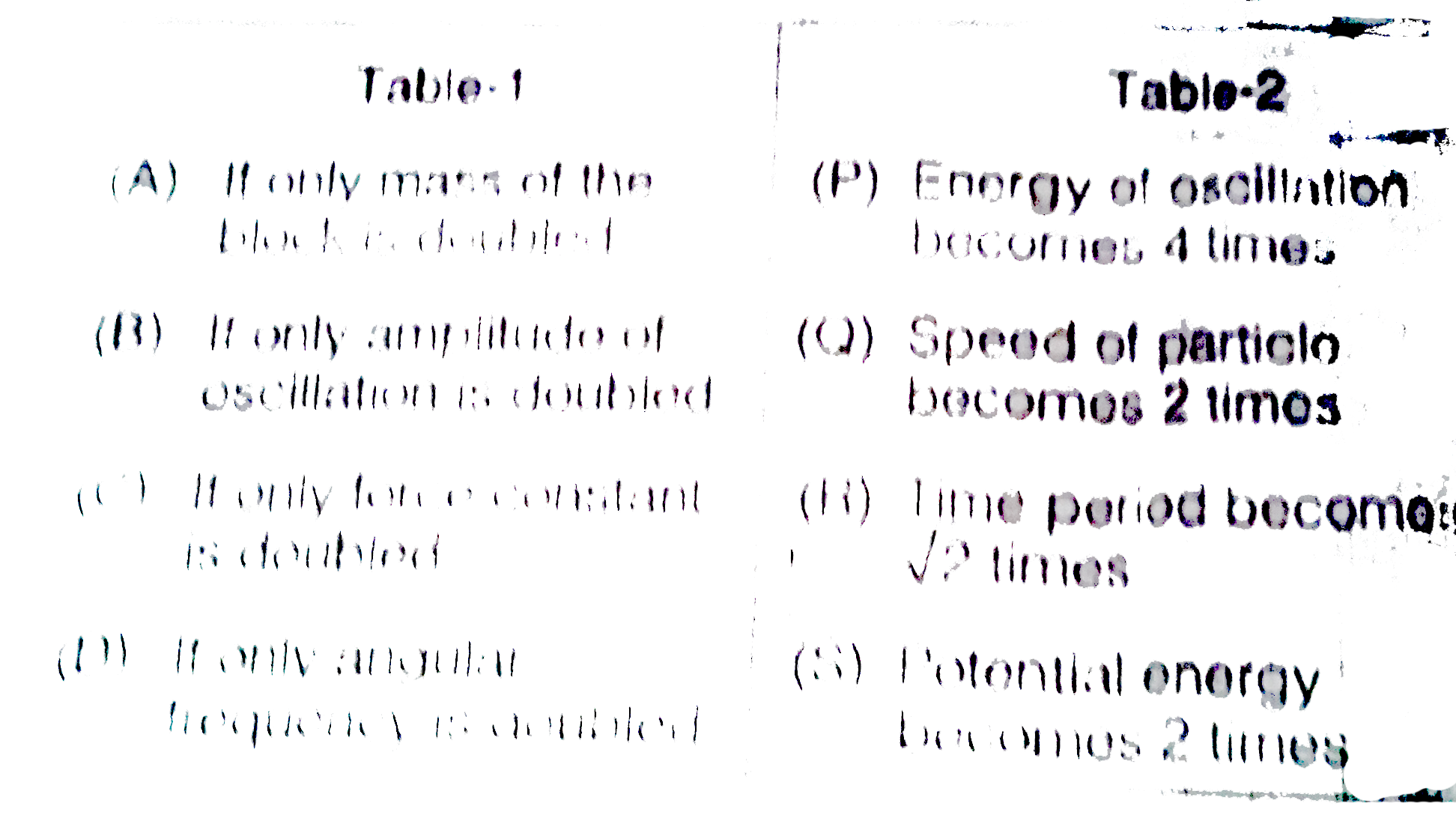
View SolutionTwo springs have their force constants in the ratio of 3:4. Both the springs are stretched by applying equal force F. If elongation in first spring is x then elogation is second spring is
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
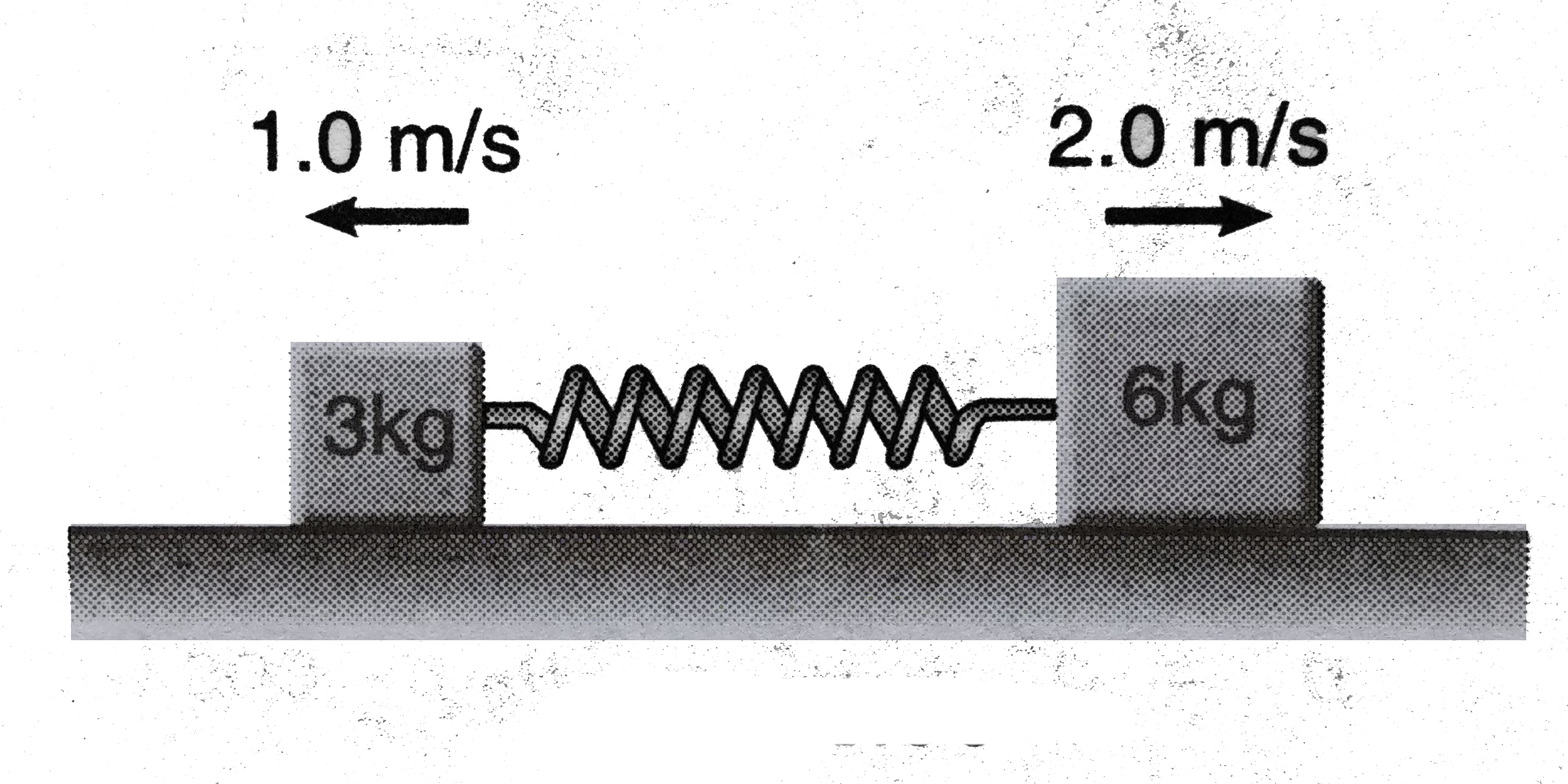
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
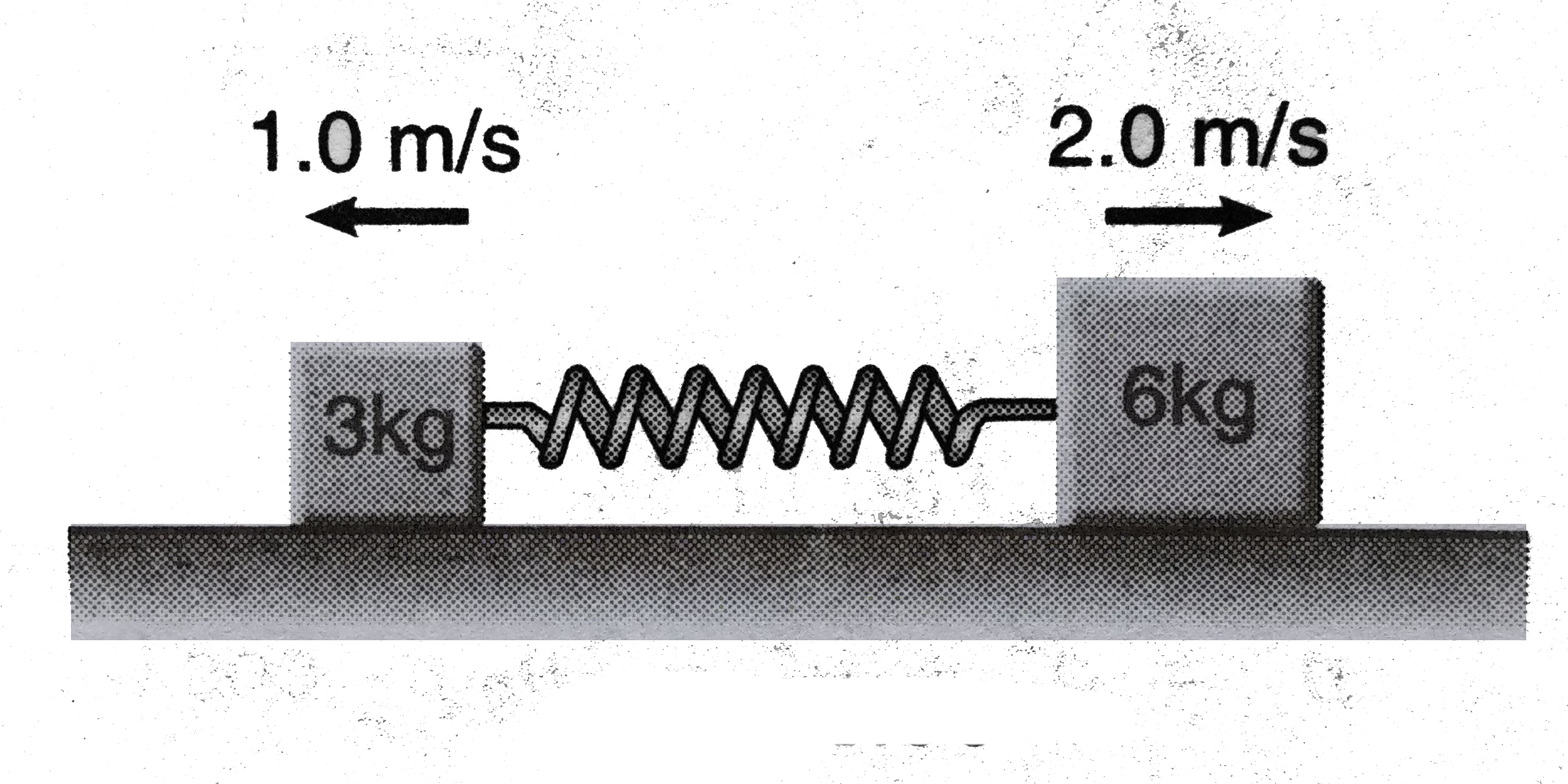
View Solution
