Comparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
CL
V1CL
CL
LC
The correct Answer is:D
Topper's Solved these Questions
Similar Questions
While comparing the L−C oscillations with the oscillations of spring-block system, with whom the magnetic energy can be compared and why?
View SolutionWhile comparing the L−C oscillations with the oscillations of spring-block system, with whom the magnetic energy can be compared and why?
View Solution
Knowledge Check
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
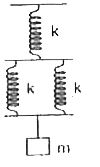A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
A2π√mkBπ√mkC4π√mkD2π√m2k
Comparing L-C oscillation with the oscillation if spring-block-system, match the following table.
Comparing L-C oscillations with the oscillations of spring-block sytem, match the following table Table-1(LC oscillations)Table-2(Spring-block oscillations)(A)L(P)k(B)C(Q)m(C)i(R)v(D)didt(S)x(T)None
View SolutionComparing L-C oscillation with the oscillation if spring-block-system, match the following table.
Comparing L-C oscillations with the oscillations of spring-block sytem, match the following table Table-1(LC oscillations)Table-2(Spring-block oscillations)(A)L(P)k(B)C(Q)m(C)i(R)v(D)didt(S)x(T)None
View SolutionFigure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
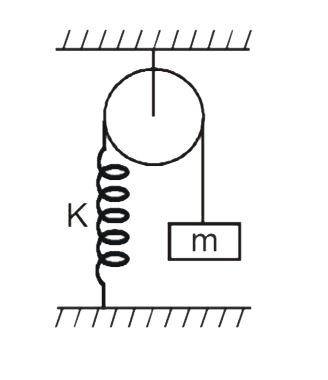
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
View SolutionAs shown in the figure a block of mass m is hung from the ceiling by the system of springs consisting of two layers. The force constant of each of the springs is k. The frequency of the vertical oscillations of the block is
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
View Solution