In the YDSE, the monochromatic source of wavelength λ is placed at a distance d2 from the central axis (as shown in the figure), where d is the separation between the two slits S1andS2 .
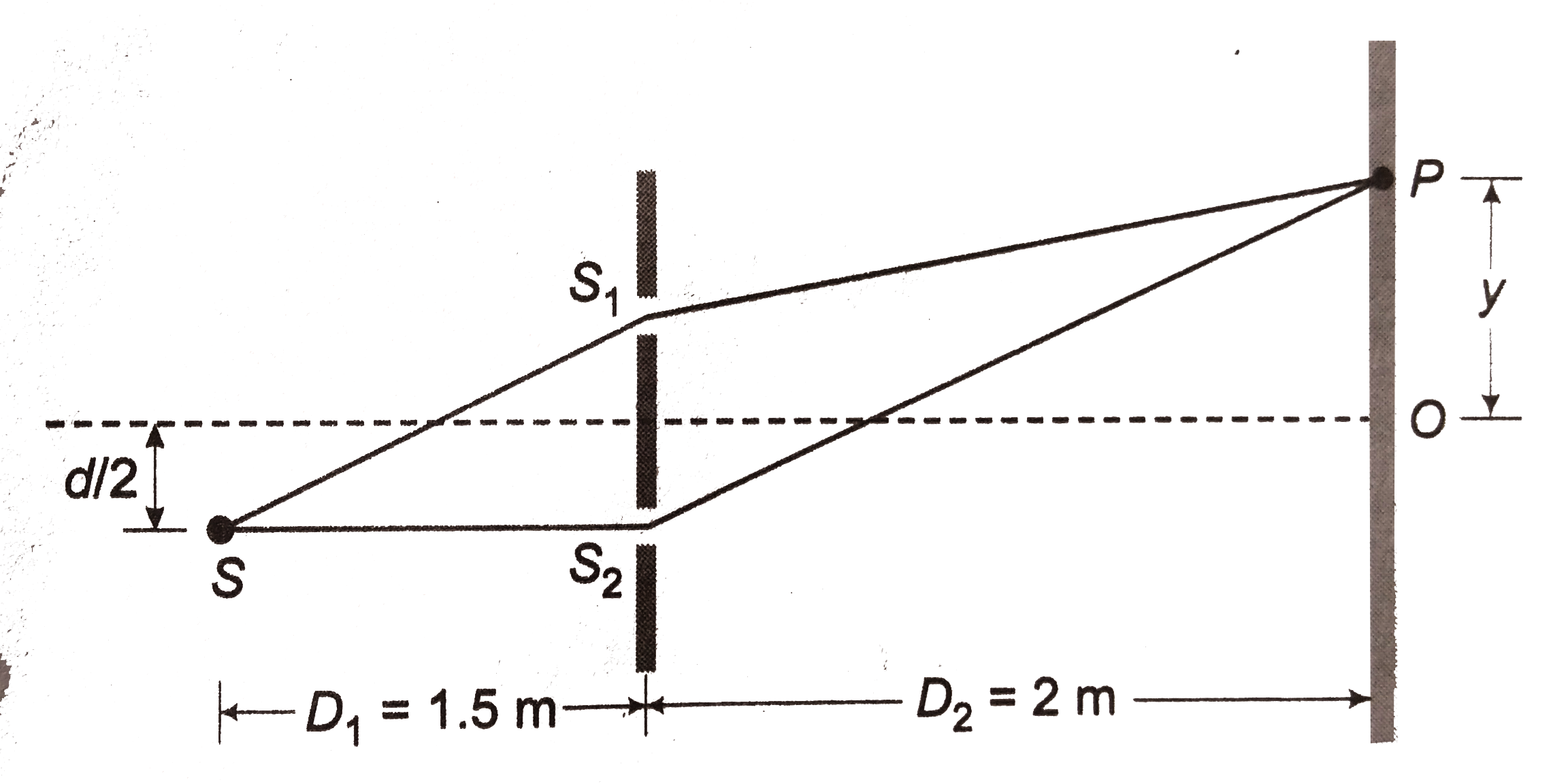
(a)Find the position of the central maxima.
(b) Find the order of interference formed at O.
(c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes μ=1.5 to be placed in front of S2 so that intensity at O becomes 34th of the maximum intensity.
(Take λ=6000Å,d=6mm.)
The correct Answer is:[(a) 4 mm above 0; (b) 20; (c ) 2000 Å]
Step by step video, text & image solution for In the YDSE, the monochromatic source of wavelength lambda is placed at a distance d/2 from the central axis (as shown in the figure), where d is the separation between the two slits S_1 and S_2 . (a)Find the position of the central maxima. (b) Find the order of interference formed at O. (c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes mu =1.5 to be placed in front of S_2 so that intensity at O becomes 3/4th of the maximum intensity. (Take lambda=6000Å, d = 6mm.) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In the YDSE the monochromatic source of wavelength λ is placed at a distance d2 from the central axis (as shown in the figure), where d is the separation between two slits S1 and S2. Find the position of the central maxima. (Given d = 6 mm)
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View SolutionLight of wavelength lambda= 500 nm falls on two narrow slits placed a distance d= 50 xx 10^(-4) cm apart, at an angle phi= 30^@ relative to the slits shown in figure. In front of the lower slit, a slab of thickness 0.1 mm and refractie index 3/2 is placed. THe interference pattern is observed on a screen at a distance D= 2m from the slits S_1 O = S_2 O = d//2 The position of central maxima is at an angular position theta with line OB
View SolutionIn the YDSE the monochronic source of wavelength λ is palced at a distance d2 from the central axis (as shown in the figure ) , where d is the separation between two slits S1andS2 .Find the position of the central maxima . (Given d = 6 mm )
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionConsider the situation shown in figure. The two slite S_1 and S_2 placed symmetrically around the centre line are illuminated by a monochromatic light of wavelength lambda. The separation between the slits is d. The light transmitted by the slits falls on a screen M_1 placed at a distance D from the slits. The slit S_3 is at the centre line and the slit S_4 is at a distance y form S_3 . Another screen M_2 is placed at a further distance D away from M_1 . Find the ration of the maximum to minimum intensity observed on M_2 if y is equal to (dltltD) .
View SolutionIn the YDSE, the monochromatic source of wavelength λ is placed at a distance d2 from the central axis (as shown in the figure), where d is the separation between the two slits S1andS2 .
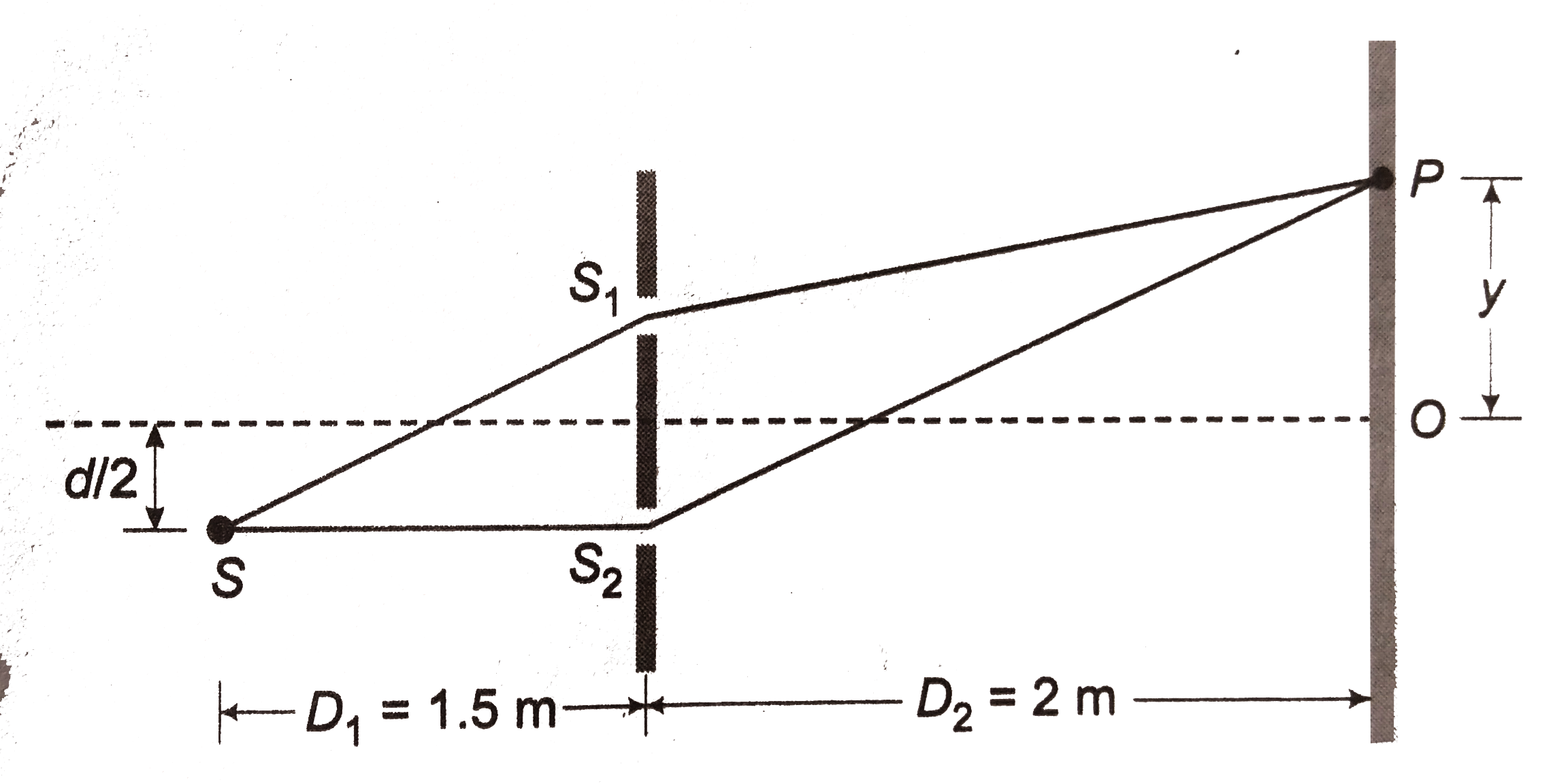
(a)Find the position of the central maxima.
(b) Find the order of interference formed at O.
(c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes μ=1.5 to be placed in front of S2 so that intensity at O becomes 34th of the maximum intensity.
(Take λ=6000Å,d=6mm.)
View Solution
