Consider the situation shown in figure. The two slite S1andS2
placed symmetrically around the centre line are illuminated by a monochromatic
light of wavelength lambda. The separation between the slits is d. The light transmitted
by the slits falls on a screen M1 placed at a distance D from the slits. The slit S3 is
at the centre line and the slit S4 is at a distance y form S3. Another screen M2 is
placed at a further distance D away from M1. Find the ration of the maximum to
minimum intensity observed on M2 if y is equal to (d<<D).
The correct Answer is:A, B, C, D
To solve the problem, we need to find the ratio of the maximum to minimum intensity observed on screen M2, given the conditions of the slits and the distances involved. Let's break down the solution step by step:
Step 1: Understanding the Setup
We have two slits S1 and S2 that are illuminated by monochromatic light of wavelength λ. The distance between the slits is d, and the distance from the slits to screen M1 is D. There are two additional slits S3 and S4, with S3 at the center line and S4 at a distance y from S3. Another screen M2 is placed at a further distance D from M1.
Hint: Visualize the arrangement of the slits and screens to understand the path differences that will affect the interference pattern.
Step 2: Path Difference at S4
The path difference between the light coming from S1 and S2 to point S4 on screen M2 can be calculated. Since S4 is at a distance y from S3, the path difference (Δ) can be approximated as:
Δ=d⋅yD
This is valid under the condition that y is much smaller than D (y << D).
Hint: Remember that the path difference is crucial for determining the interference pattern.
Step 3: Conditions for Maximum and Minimum Intensity
1. Maximum Intensity (I_max) occurs when the path difference is an integer multiple of the wavelength:
Δ=nλ(n=0,1,2,…)
2. Minimum Intensity (I_min) occurs when the path difference is an odd multiple of half the wavelength:
Δ=(n+12)λ(n=0,1,2,…)
Hint: Use the conditions for constructive and destructive interference to find the respective intensities.
Step 4: Calculating Intensities
The intensity at any point on the screen can be expressed in terms of the amplitudes of the waves coming from the slits. If we denote the amplitude from each slit as A, the resultant amplitude at S4 can be calculated for both maximum and minimum conditions.
1. For maximum intensity:
Imax=(A1+A2)2=(2A)2=4A2
2. For minimum intensity:
Imin=(A1−A2)2=(0)2=0(when they cancel each other)
Hint: Remember that the intensity is proportional to the square of the amplitude.
Step 5: Finding the Ratio
The ratio of maximum to minimum intensity can be calculated as:
ImaxImin=4A20(undefined, since minimum intensity cannot be zero)
However, if we consider the case where the amplitudes do not cancel completely, we can express the ratio in terms of the amplitudes:
ImaxImin=(2A)2(A−A)2
This leads to a more general case where we can find a finite value based on the specific amplitudes involved.
Hint: Be cautious with the minimum intensity; it should not be zero in practical scenarios.
Final Answer
The ratio of the maximum to minimum intensity observed on M2 can be expressed as:
ImaxImin=finite value based on specific amplitudes
We have two slits S1 and S2 that are illuminated by monochromatic light of wavelength λ. The distance between the slits is d, and the distance from the slits to screen M1 is D. There are two additional slits S3 and S4, with S3 at the center line and S4 at a distance y from S3. Another screen M2 is placed at a further distance D from M1.
The path difference between the light coming from S1 and S2 to point S4 on screen M2 can be calculated. Since S4 is at a distance y from S3, the path difference (Δ) can be approximated as:
Δ=d⋅yD
This is valid under the condition that y is much smaller than D (y << D).
1. Maximum Intensity (I_max) occurs when the path difference is an integer multiple of the wavelength:
Δ=nλ(n=0,1,2,…)
2. Minimum Intensity (I_min) occurs when the path difference is an odd multiple of half the wavelength:
Δ=(n+12)λ(n=0,1,2,…)
The intensity at any point on the screen can be expressed in terms of the amplitudes of the waves coming from the slits. If we denote the amplitude from each slit as A, the resultant amplitude at S4 can be calculated for both maximum and minimum conditions.
Imax=(A1+A2)2=(2A)2=4A2
2. For minimum intensity:
Imin=(A1−A2)2=(0)2=0(when they cancel each other)
The ratio of maximum to minimum intensity can be calculated as:
ImaxImin=4A20(undefined, since minimum intensity cannot be zero)
However, if we consider the case where the amplitudes do not cancel completely, we can express the ratio in terms of the amplitudes:
ImaxImin=(2A)2(A−A)2
This leads to a more general case where we can find a finite value based on the specific amplitudes involved.
The ratio of the maximum to minimum intensity observed on M2 can be expressed as:
ImaxImin=finite value based on specific amplitudes
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - type-5
1 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 6
3 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 4
1 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
Consider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

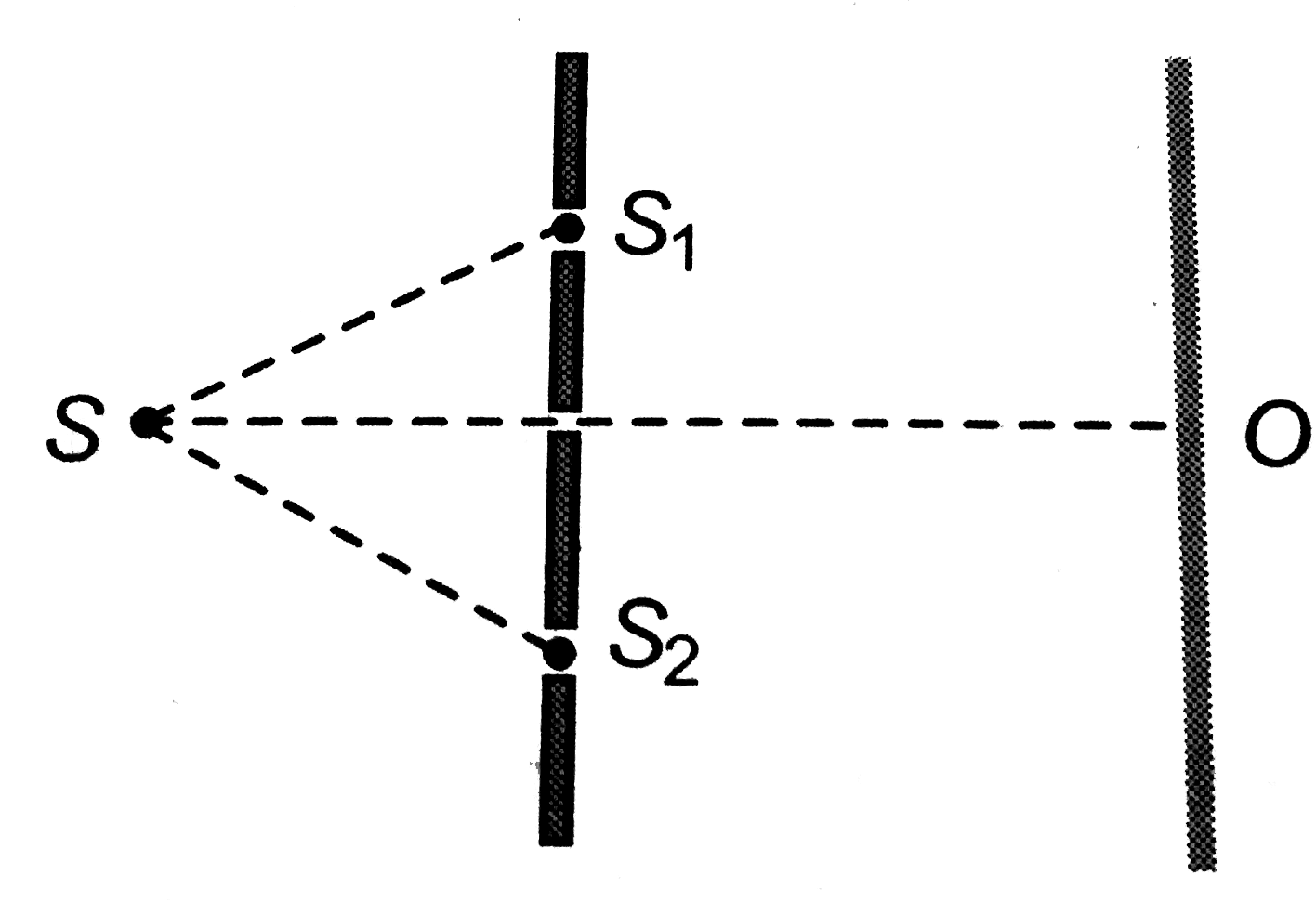
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
View Solution
Knowledge Check
In a double slit experiment, the distance between the slits is d. The screen is at a distance D from the slits. If a bright fringe is formed opposite to one of the slits, its order is
AdλBλ2dDCD22λDDd22Dλ
Young’s double slit experiment is performed with light of wavelength 550 nm . The separation between the slits is 1.10mm and screen is placed at distance of 1 m . What is the distance between the consecutive bright or dark fringes
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View SolutionIn Yonung's double-slit experiment, two slits which are separated by 1.2 mm are illuminated with a monochromatic light of wavelength 6000Å The interference pattern is observed on a screen placed at a distance of 1 m from the slits. Find the number of bright fringes formed over 1 cm width on the screen.
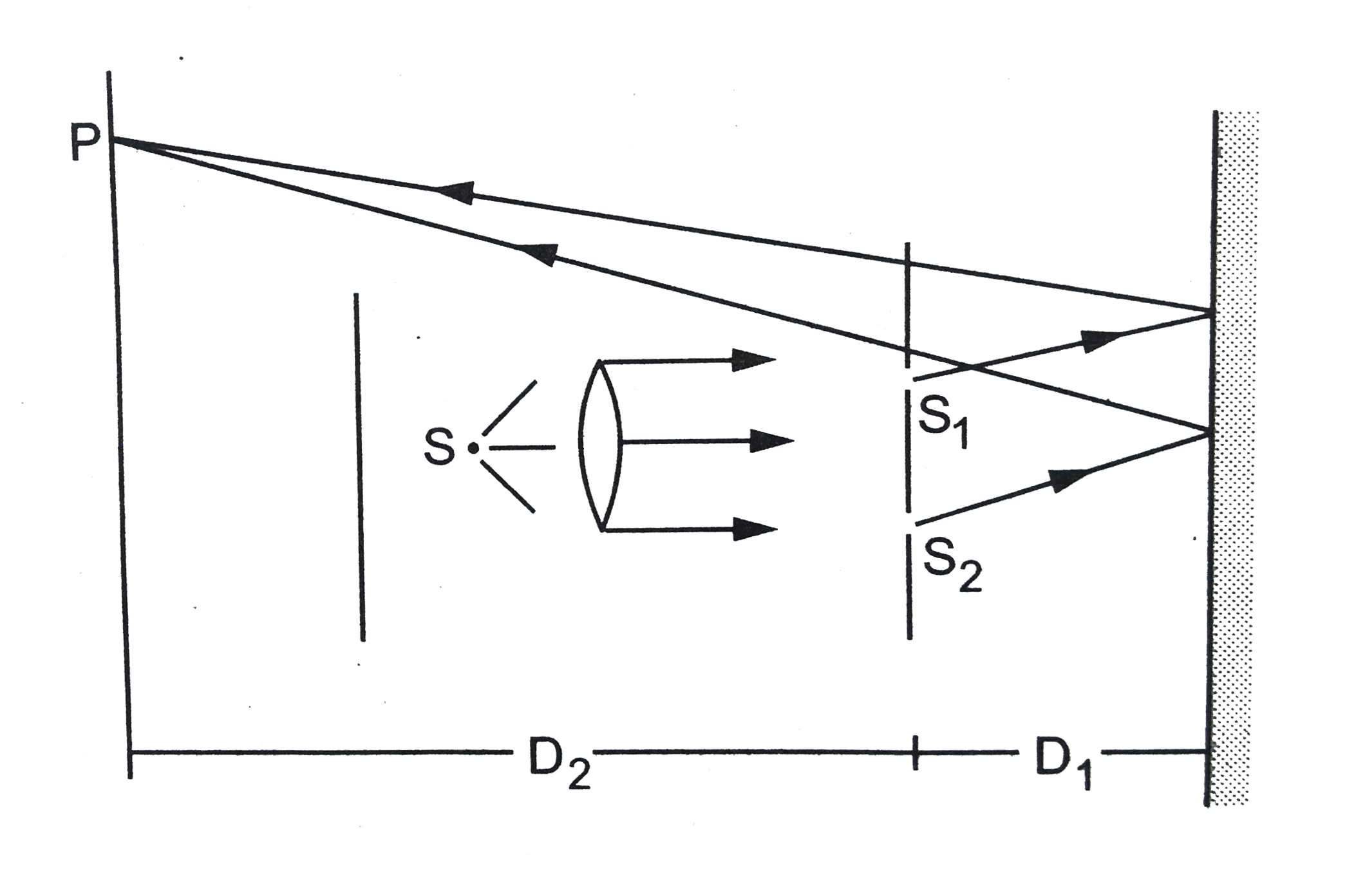
View SolutionA double slit S1−S2 is illuminated by a coherent light of wavelength λ. The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1, from it and a screen ∑ is placed behind the double slit at a distance D2, from it . The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
View SolutionTwo slits, 4 mm apart, are illuminated by light of wavelength 6000Å. What will be the fringe width on a screen placed 2 m from the slits
View SolutionWhite light is used to illuminate the two slits in a Young's
double slit experiment. The separation between the slits is b and the screen is at
a distance d(>>b) from the slits. At a point on the screen directly in front of
one of the slits, certain wavelengths are missing. Some of these missing
wavelength are
View Solution
