Consider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

The correct Answer is:A, B, C, D
i. when z=Dλ2d,atS4
minimum intensilty occurs, (dark fringe)
→Amplitude=0
At S3 path differenc e=0<br>→maxiμm∫ensityours.<br>→Amplitude=2r<br>SoonSigma^2screen,<br>l_(max)/l_(min)=((2r+0)^2)/((2r-0)^2)=1<br>ii.Whenz=λDd
As S4 maximum intensity occurs
→Amplitude=√2r
At S3 also maximum intensity occurs.
lmaxlmin=(2r+2r)2(2r−2r)2=∞
iii When z=λD4d,atS4
intensity =l_(max)/2<br>rarr Amplitude=sqrt2r<br>:. At S_3Intensi<yisminiμm<br>rarr Amplitude =2r
lmaxlmin=(2r+√2r)2(2r−√2r)2=34
Topper's Solved these Questions
Similar Questions
Consider the situation shown in figure. The two slite S1andS2
placed symmetrically around the centre line are illuminated by a monochromatic
light of wavelength lambda. The separation between the slits is d. The light transmitted
by the slits falls on a screen M1 placed at a distance D from the slits. The slit S3 is
at the centre line and the slit S4 is at a distance y form S3. Another screen M2 is
placed at a further distance D away from M1. Find the ration of the maximum to
minimum intensity observed on M2 if y is equal to (d<<D).
View SolutionConsider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d
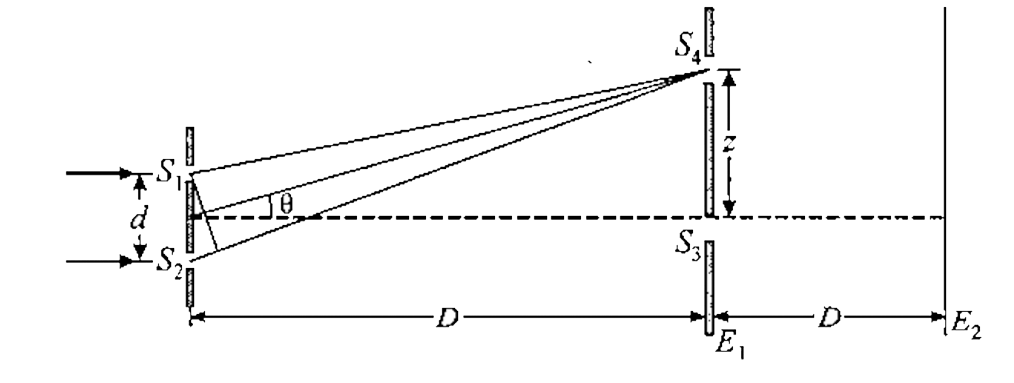
View Solution
Knowledge Check
Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
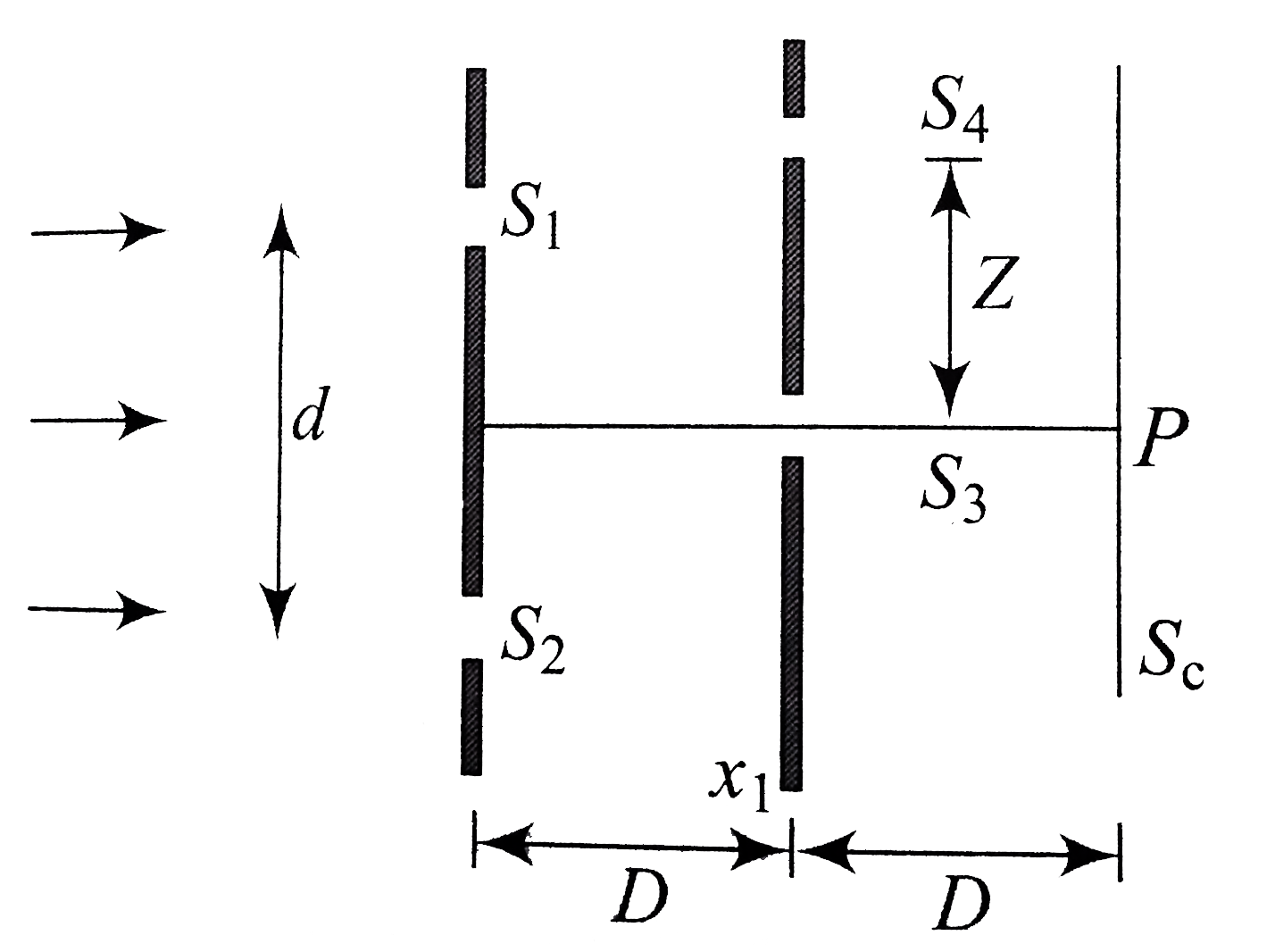
If z=λD4dA[3−2√2]2B[3+√2]2C[3−√2]2D[3+2√2]2Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
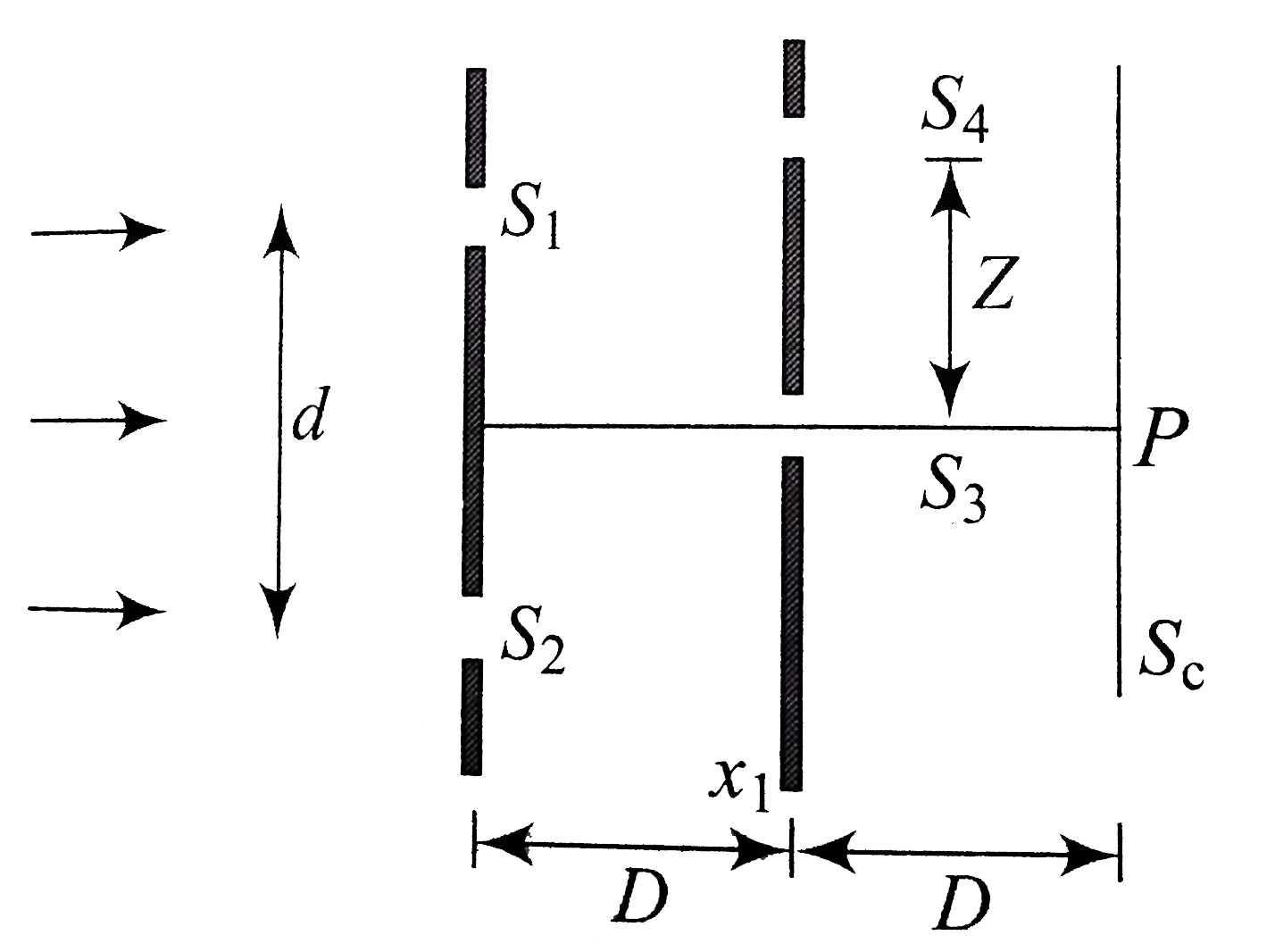
If z=λD2dA1B1/2C3/2D2Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
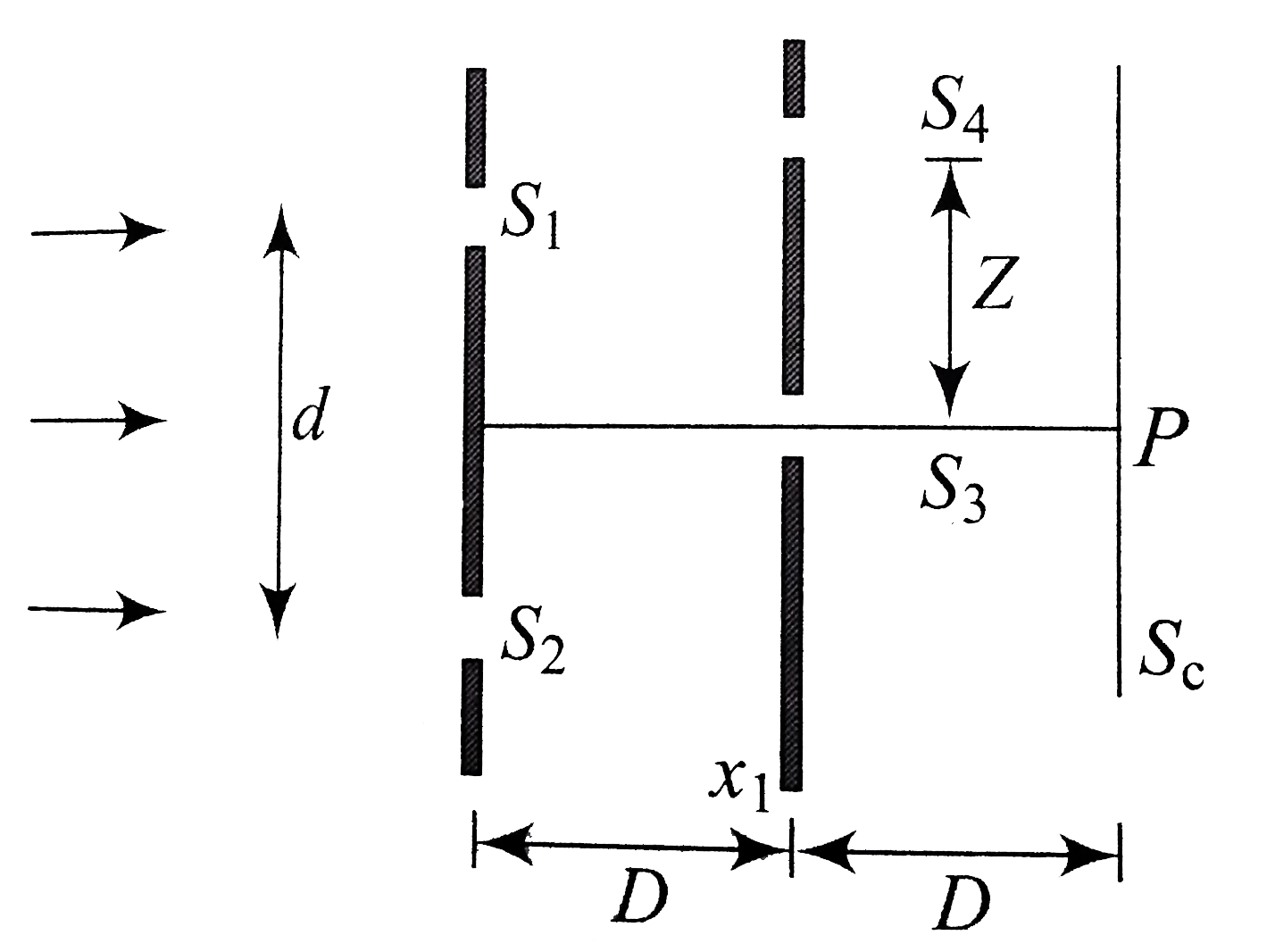
If z=λDdA4B2C∞D1
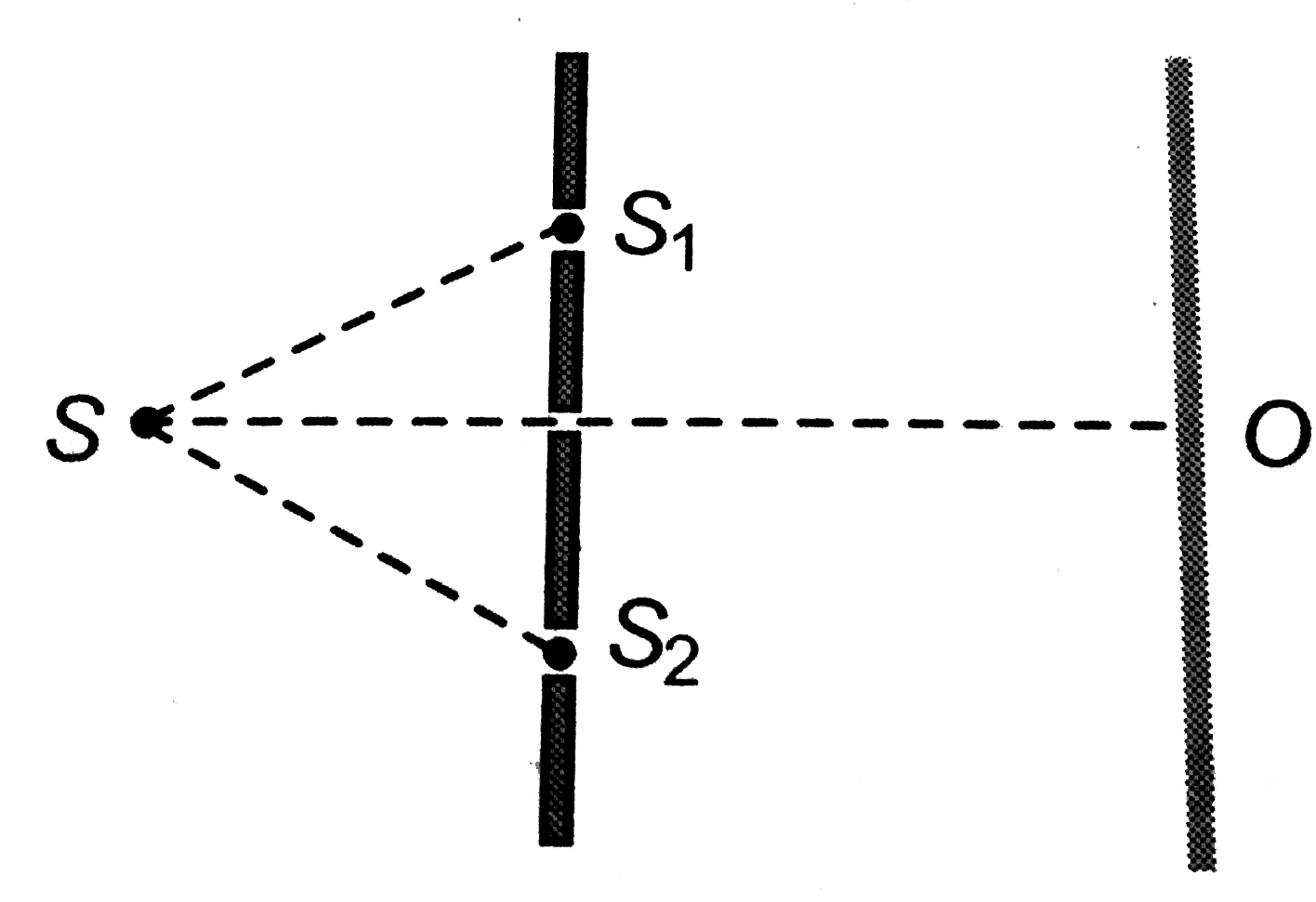
In the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
View SolutionYoung’s double slit experiment is performed with light of wavelength 550 nm . The separation between the slits is 1.10mm and screen is placed at distance of 1 m . What is the distance between the consecutive bright or dark fringes
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then

View SolutionYoung’s double slit experiment is performed with light of wavelength 550 nm . The separation between the slits is 1.10mm and screen is placed at distance of 1 m . What is the distance between the consecutive bright or dark fringes
View Solution_E01_037_Q01.png)
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 3λ the light is collected on a screen S which is placed at a distance D(>>λ) from the slits the smallest distance x such that the P is a maxima.
View Solution
