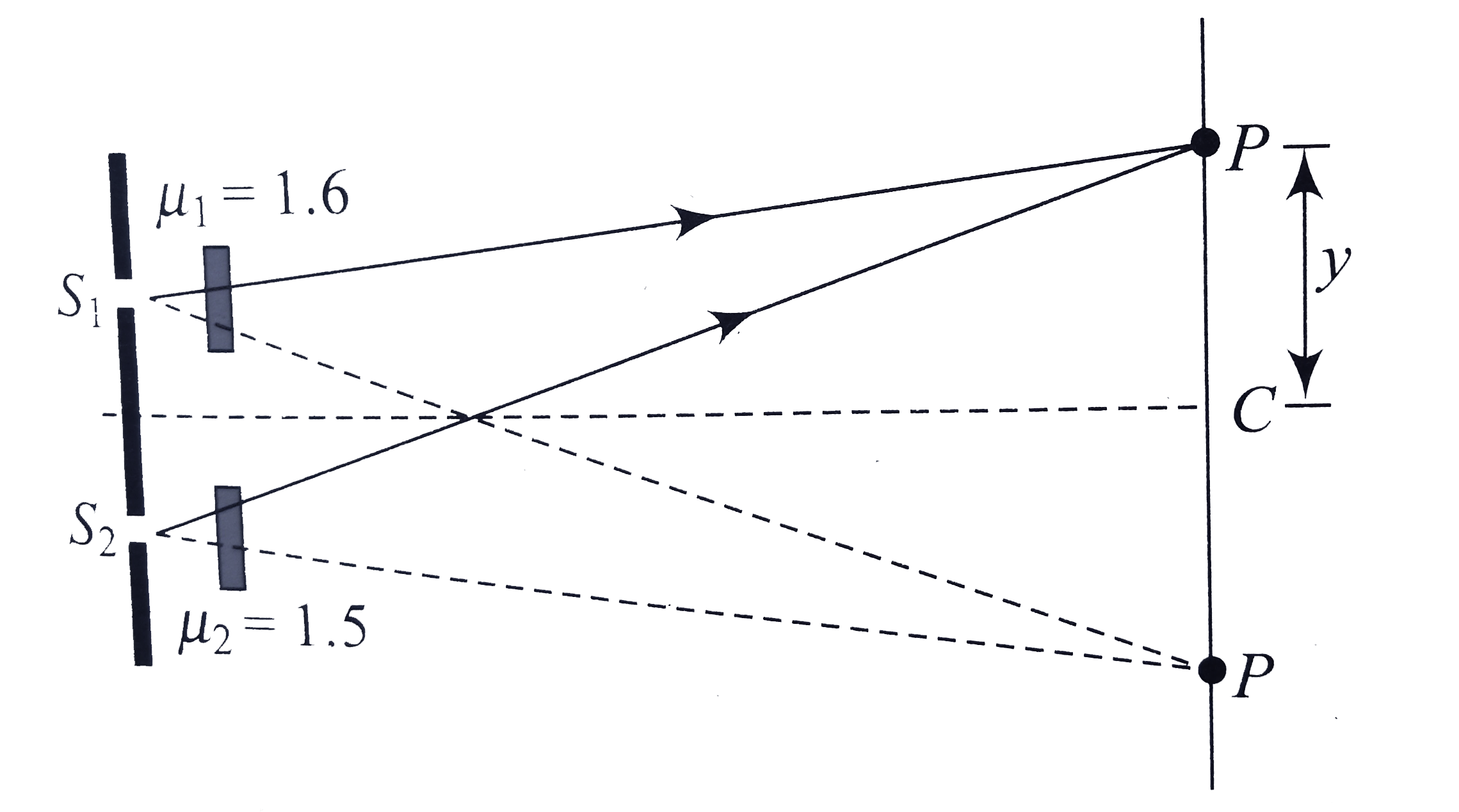
In the Young's double-slit experiment, the amplitude os source S1 is three times the amplitude of the source S2. These sources are covered by perfectly transparent thin plates of same thickness but different refractive indices 1.6 and 1.5, respectively. Now, if the plates are interchanged and the amplitude of source S1 is made same as that of S2, then find the amout by which the intensity is changed at a point where previous central maxima was formed. Take thickness of the plate equal to (110/3)λ, where λ is the wavelength of light used.
The correct Answer is:116
Ratio of intensities of the sources S1 and S2,
I1I2=9
Let I2=I0 and I1=9I0.
Intensity at any point on the screen.
I=9I0+I0+2√9I0I0cosγ
For maxima at P,
I=2I0[5+2]=16I0
If transparent plates are interchanged, the central maxima will shift downward by some amout j.
j=Dt(μ1−μ2)d
Δxp=ydD+t(μ2−μ1)=0
⇒ydD=t(μ1−μ2)
When μ2 and μ1 are interchanged
Δxp1=ydDt(μ1−μ2)=2t(μ1−μ3)
Phase diffenence at P,
ϕ=2πλ2(μ1−μ2)t=443π
Now, intensity at P,
I'=I+I0+2I0cos(443)π−I0
Hence, ratio of intensities at P,
I'I=I016I0=116
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Single Correct
128 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.2
22 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
Microwaves from a transmitter are directed normally toward a plane reflector. A detector moves along the normal to the reflector. Between positionsof 14 m successive maxima the detector travels a distance 0.14 m. The frequency of the transmitter is (c=3×108ms−1).
View SolutionIn Young's double-slit experiment, two wavelengths of light are used simultaneously where λ2=2λ1. In the fringe pattern observed on the screen,
View SolutionIn Young's double slit experiment with wavelength 5890 Å, there are 60 fringe in the field of vision, How many fringes will be observed in the same field of vision id wavelength used is 5460 Å?
View SolutionThe figure shows two paths through which a gas can be taken from state A to state B. If the ratio of work done by the gas in the two paths is xy, then find (x+y).
'(##CEN_KSR_PHY_JEE_C15_E01_001_Q01##)'
View SolutionA string of length 1m fixed at both ends is vibrating in 3rd overtone. Tension in string is 200N and linear mass density is 5 gmin. Frequency of these vibrations is (in Hz ).
View SolutionIn a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
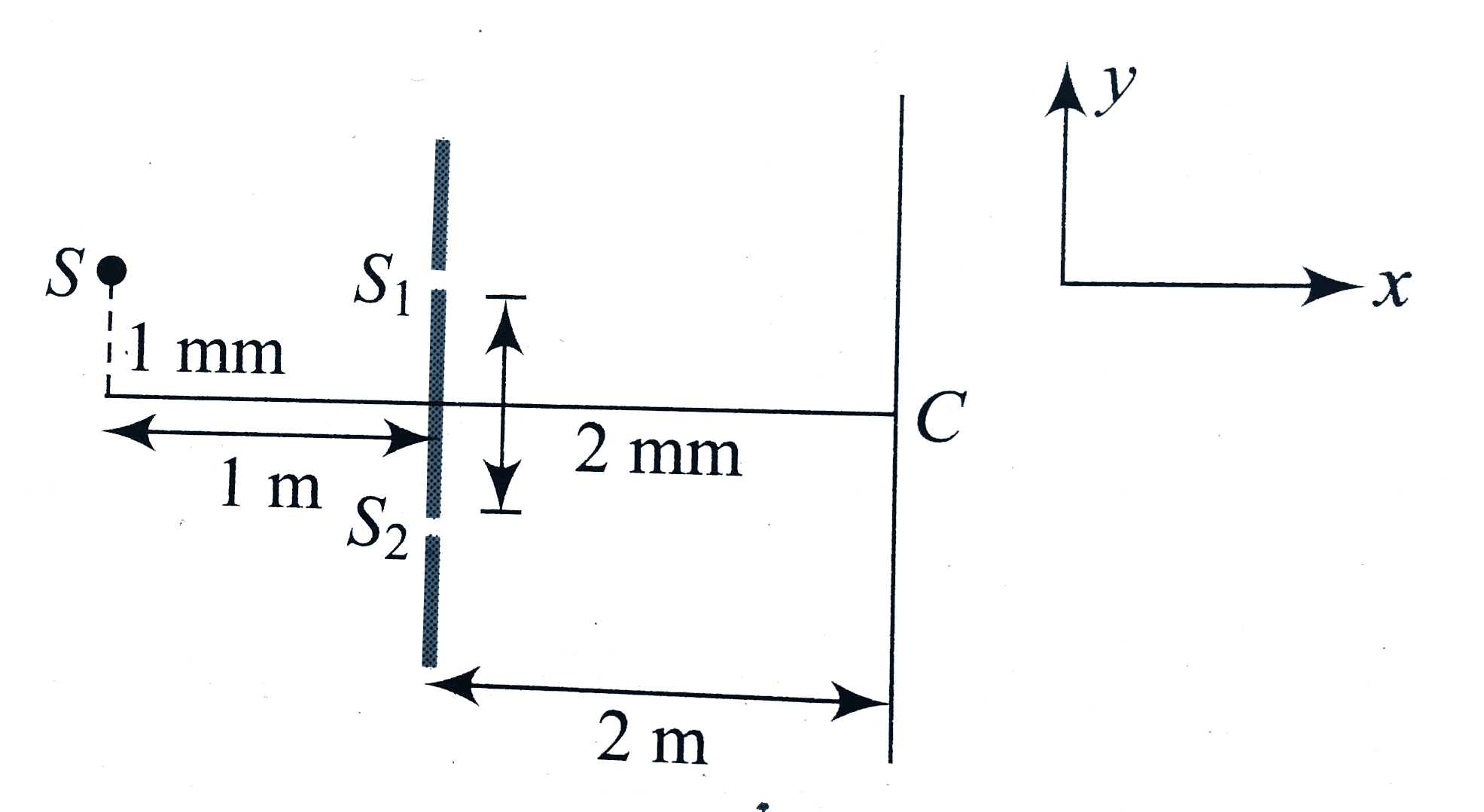
At t=1 s, a slab of thickness 2×10−3mm an refractive index 1.5 is placed just in front of S1. The central maximum is formed at
View SolutionIn a midified YDESE, sources S is kept in front of slit S_(1) . Find the phase difference at point O that is equidistant from slits S_(1) and S_(2) and point P that is in front of slit S_(1) in the following situations. ltgt Liquid is filled between the slit and source S.
View SolutionFind the ratio of intensities at the two points XandY on a screen in Young's double slit experiment, where waves from the two source S1andS2 have path difference of zero, and λ/4 respectively.
View SolutionIf y=5(mm)sinπt is equation of oscillation of source S1 and y2=5(mm)sinπ/6) be that of S2 and it takes 1sec and ^(1/2sec for the transverse waves to reach point A from source S1 and S2 respectively then the resulting amplitude at point A, is
_S01_006_Q01.png) .
.
View SolutionThree coherent sources S_(1), S_(2)" and" S_(3) can throw light on a screen. With S_(1) switched on intensity at a point P on the screen was observed to be I. With only S_(2) on, intensity at P was 2I and when all three are switched on the intensity at P becomes zero. Intensity at P is I when S_(1)" and" S_(2) are kept on. Find the phase difference between the waves reaching at P from sources S_(1) "and" S_(3) .
View SolutionIn the figure shown S_(1)O-S_(2)O=S_(3)O-S_(2)O=(lambda)/(4) , Intensity at O due to any one of the slits is I_(0) . What is the intensity due to all the three coherent sources S_(1), S_(2) and S_(3) ?
View Solutionधवनि की तीन स्त्रोत S1,S2 तथा एS3 क ही रेखा में रखे हुए है -S1S2=S2S3 है और तीनो एक ही त्रीवता की धवनि उत्पन कर रखे हुए है S1S2=S2S3 है और तीनो एक ही त्रीवता की धवनि उत्पन्न क्र रहे है इसी रेखा पर इन स्त्रोत से बहुत दूर के एक बिंदु P पर S2 से आती रंग S1 से आती तरंग से 120∘ आगे की कला पर है तथा S3 से आती तरंग S2 से आती रंग से 120∘ आगे की कला पर है P बिंदु पर धवनि की परिणामी त्रीवता क्या होगी

View SolutionS1andS2 are two coherent sources. The intensity of both sources are same. If the intensity at the point of maxima is 4Wm−2, the intensity of each source is
View SolutionTwo sound waves each of wavelength λ and having the same amplitude A form two sources S1andS2 interfere at a point P. If the path difference S2P−S1P=λ3, then the amplitude of the resultant were at P will be
View SolutionIn an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
View Solution
