In this problem an object is pulled along a ramp but the object starts and ends at rest and thus has no overall change in its kinetic energy ( that is important). Figure 8-10a shows the situation. A rope pulls a 200 kg sleigh ( which you may know) up a slope at incline angle θ=30∘, through distance d=20 m. The sleigh and its contents have a total mass of 200 kg. the snowy slope is so slippery that we take it to be frictionless. How much work is done by each force acting on the sleigh ?
KEY IDEAS
(1) During the motion, the forces are constant in magnitude and direction and thus we can calculate the work done by each with Eq. 8-7 (W=Fdcosϕ) in which ϕ is the angle between the force and the displacement. We reach the same result with Eq. 8-8 (W=→F⋅→d) in which we take a dot product of the force vector and displacement vector. (2) We can relate the net work done by the forces to the change in kinetic energy energy ( or lack of a change, as here) with the work-kinetic energy theorem of Eq. 8-10 (ΔK=W).
Calculations: The first thing to do with most physics problems involving forces is to draw a free-body diagram to organize our thoughts. For the sleigh, Fig, 8-10b is our free-body diagram, showing the gravitational force →Fg, the force →T from the rope, and the normal force →FN from the slope.
Work WN by the normal force, Let.s start with this easy calculation. The normal force is perpendicular to the
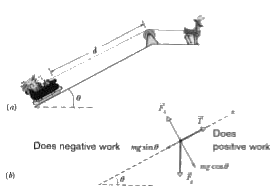
Figure 8-10 (a) A sleigh is pulled up a snowy slope. (b) The freebody diagram for the sleigh.
slope and thus also to the sleigh.s displacement. Thus the normal force does not affect the sleigh.s motion and does zero work. To be more formal, we can apply Eq. 8-7 to write
WN=FNdcos90∘=0.
Work Wg by the gravitational force. We can find the work done by the gravitational force in either of two ways (you pick the more appealing way). From an earlier discussion about ramps (Sample Problem 5.06 and Fig. 5-23), we know that the component of the gravitational force along the slope has magnitude mg sinθ and is directed down the slope. Thus the magnitude is
Fgx=mgsinθ=(200kg)(9.8m/s2)sin30∘
=980N.
The angle ϕ between the displacement and this force component is 180∘ . So we can apply Eq. 8-7 to write
Wg=Fgxdcos180∘=(980N)(20m)(−1)
=−1.96×104J.
The negative result means that the gravitational force removes energy from the sleigh.
The second (equivalent) way to get this result is to use the full gravitational force →Fg instead of a component. The angle between →Fg and →d is 120∘ (add the incline angle 30∘ to 90∘). So, Eq. 8-7 gives us
Wg=Fgdcos120∘=mgdcos120∘
=(200kg)(9.8m/s2)(20m)cos120∘
=1.96×104J.
Work WT by the rope.s force. We have two ways of calculating this work. The quickest way is to use the work-kinetic energy theorem of Eq. 8-10 (ΔK=W), where the net work W done by the forces is WN+Wg+WT and the change ΔK in the kinetic energy is just zero (because the initial and final kinetic energies are the same-namely, zero). So, Eq. 8-10 gives us
0=WN+Wg+WT=0−1.96×104J+WT
and WT=1.96×104J.
Instead of doing this, we can apply Newton.s second law for motion along the x axis to find the magnitude FT of the rope.s force. Assuming that the acceleration along the slope is zero (except for the brief starting and stopping), we can write
Fnet. x=max,
FT−mgsin30∘=m(0),
to find
FT=mgsin30∘.
This is the magnitude. Because the force and the displacement are both up the slope, the angle between those two vectors is zero. So, we can now write Eq. 8-7 to find the work done by the rope.s force:
WT=FTdcos0∘=(mgsin30∘)dcos0∘
=(200kg)(9.8m/s∘)(sin30∘)(20m)cos0∘
=1.96×104J.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
Knowledge Check
An object of 1kg mass has a momentum of 10 kg m / sec then the kinetic energy of the object will be
A100JB50JC1000JD200JAn object is acted on by a retarding force of 10N and at a particular instant its kinetic energy is 6J. The object will come to rest after it has travelled a distance of
A3/5B5/3C4mD16mA lawn roller is pulled along a horizontal surface through a distance of 20m by a rope with a force of 200N. If the rope makes an angle of 60∘ with the vertical while pulling, the amount of work done by pulling force is
A4000 JB1000 JC2000√3JD2000 J
A box is projected up a long ramp (incline angle with the horizontal=30∘) with an initial speed of 8m/s. if the surface of the ramp is very smooth (essentially frictionless), how high up the ramp will the box go? What distance along the ramp will it slide?
View SolutionIn Fig. 5-23a, a cord pulls a box of sea biscuits up along a frictionless plane inclined at angle θ=30.0∘. The box has mass m = 5.00 kg, and the force from the cord has magnitude T = 25.0 N. What is the box's acceleration a along the inclined plane ?
View SolutionA constant force of 20N is applied to pull a body of mass 10 k, kept on a smooth horizontal surface. What is the increase in its kinetic energy if the body starts from rest and covers a distance of 5m?
View SolutionAn object of mass 2 kg has linear momentum magnitude 6 kg⋅m/s. What is this object's kinetic energy?
View SolutionAn object of mass 20 kg is moving with a uniform velocity of 8ms−1 . The kinetic energy possessed by the object is :
View Solution
