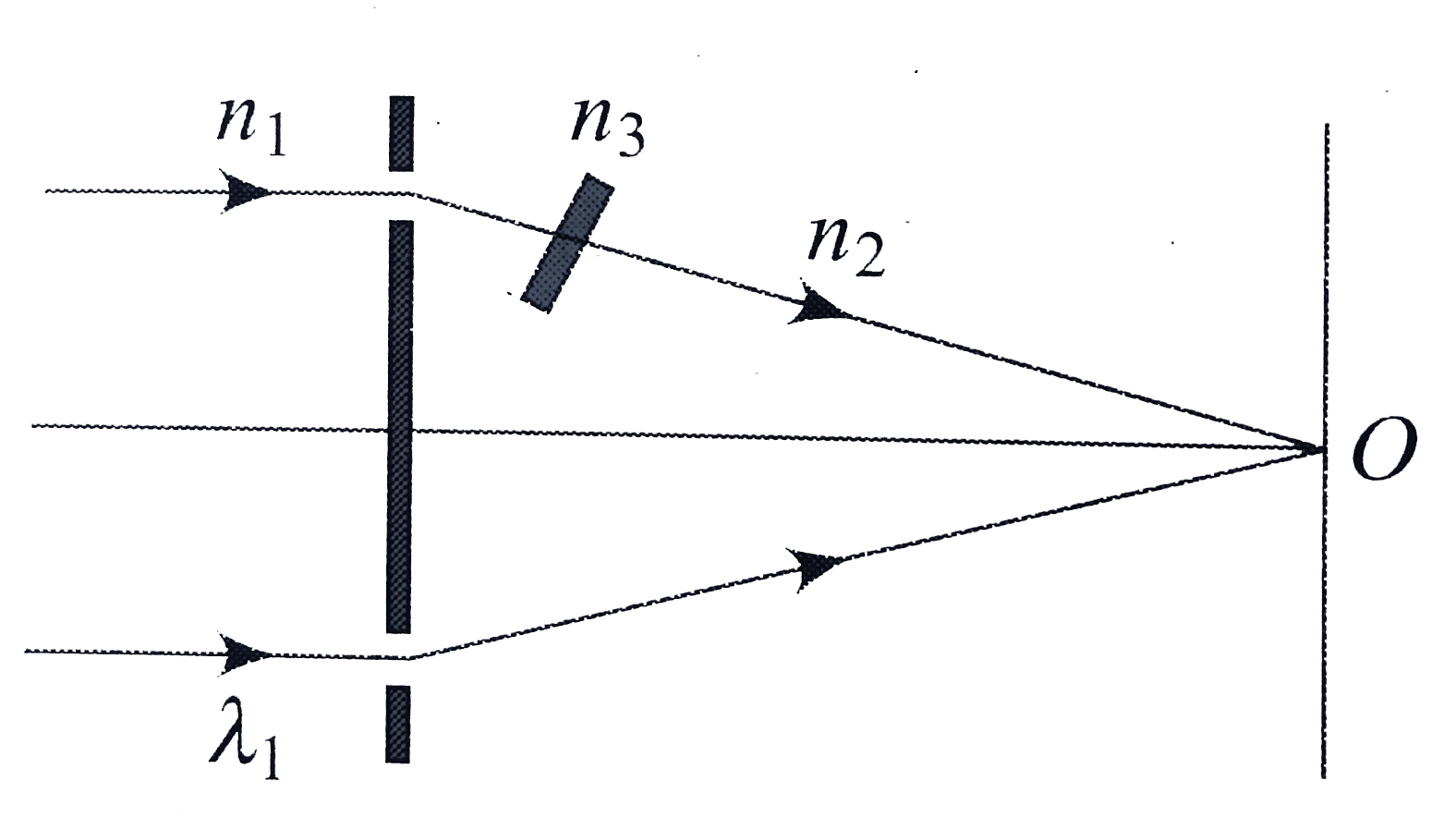
In YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index n1. The wavelength of light in this medium is λ1. A transparent of thickness t and refractive index n3 is put in front of one slit. The medium between the screen and the plane of the slits is n2. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
A
2πn1λ1(n3−n2)t
B
2πλ1(n3−n2)t
C
2πn1n2λ1(n3n2−1)t
D
2πn1λ1(n3−n2)t
Video Solution
Text Solution
The correct Answer is:a
Optical path difference the waves =(n3−n2)t
∴ Phase difference =2π(n3−n2)tλvacuum=2π(n3−n2)tn1λ1
|
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
Knowledge Check
A light wave enters from air into a medium of refractive index 1.5 . The speed of light in the medium will be
A2×108m/sB4.5×108m/sC3×108m/sDnone of theseA light wave enters from air into a medium of refractive index 1.5. The speed of light in the medium will be
A2×108m/sB4.5×108m/sC9×108m/sD(330/1.5)×108m/sThe wavelength of light in vacuum is λ. The wavelength of light in a medium of refractive index n will be
AnλBλnCλn2Dn2λ
A ray of light travelling in air is incident at 45∘ on a medium of refractive index √2. The angle of refractive in the medium is
View SolutionA beam of monochromatic light is refacted from vacuum into a medium of refracticve index 1.5 The wavelength of refracted light will be
View SolutionIf the refractive index of a medium is 1.7, the velocity of light in that medium is
View SolutionThe speed of light in a medium of refractive index 1.5 is ________.
View SolutionAN unpolarised beam of light is incident at the polarising angle on the surface of a transparent medium of refractive index 1.6. The angle of refraction in the medium is
View Solution
