In YDSE, if a bichromatic light having wavelengths λ1 and λ2 is used, then maxima due to both lights will overlaps at a certain distance y from the central maxima. Take separation between slits as d and distance between screen and slits as D. Then the value of y will be
(λ1+λ22D)d
λ1−λ2D×2d
LCM of λ1Dd and λ2Dd
HCF of λ1Dd and λ2Dd
The correct Answer is:c
Let nth1 maxima corresponding to λ1 be over lapping with nth2 maxima corresponding to λ2. Then, the required distance
y=n1y1Dd=n2λ2Dd
= LCM of λ1Dd and λ2Dd
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
Bichromatic light is used in YDSE having wavelengths λ1=400nm and λ2=700nm Find minimum order of λ1 which overlaps with λ2
View SolutionIn a double slit experiment, lo is the intensity of the central bright fringe obtained with monochromatic light of λ=6000A∘. Determine the intensity at a distance of 4.8xx10^(-5) m from the central maximum if the separation between the slits is 0.25 cm and the distance between the screen and the double slit is 1.20 m.
View Solution
Knowledge Check
Light of wavelength λ is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is ––
Ad2λB2dλC2d2λDd22λIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
A3.9mmB4.7mmC5.9mmD3.7mmIn a Young's double-slit experiment, if the incident light consists of two wavelengths λ1 and λ2, the slit separation is d, and the distance between the slit and the screen is D, the maxima due to each wavelength will coincide at a distance from the central maxima, given by
Aλ1+λ22DdBLCM of λ1d and λ2DdC(λ1−λ2)2DdDHCF of λ1D2d and λ2Dd
Bichromatic light is used in YDSE having wavelengths
λ1=400nmandλ2=700nm. Find minimum order of bright fringe of λ1
which overlaps with bright fringe of λ2 .
View SolutionIn a Young's double slit experiment, one of the slits is covered by a thin film of thickness t=0.04 mm, and refractive index μ=1.2+9×10−14m2λ2, where λ is the wavelength in meter. A beam of light consisting of two wavelength λ1=400nmandλ2=600nm falls normally on the plane of the slits. Find the distance between two central maxima in milimeter. Distance of screen from slits is 400 times the the separation between the slits.
View SolutionIn a Young's double slit experiment, if the incident light consists of two wavelengths λ1andλ2, the slit separation is d, and the distance between the slit and the screen is D, the maxima due to the two wavelengths will coincide at a distance from the central maxima, given by :
View SolutionIn a single slit diffraction of light of wavelength λ by a slit of width e, the size of the central maximum on a screen at a distance b is
View SolutionIn YDSE apparatus shown in figure wavlength of light used is λ. The screen is moved away form the source with a constant speed v. Initial distance between screen and plane of slits was D.
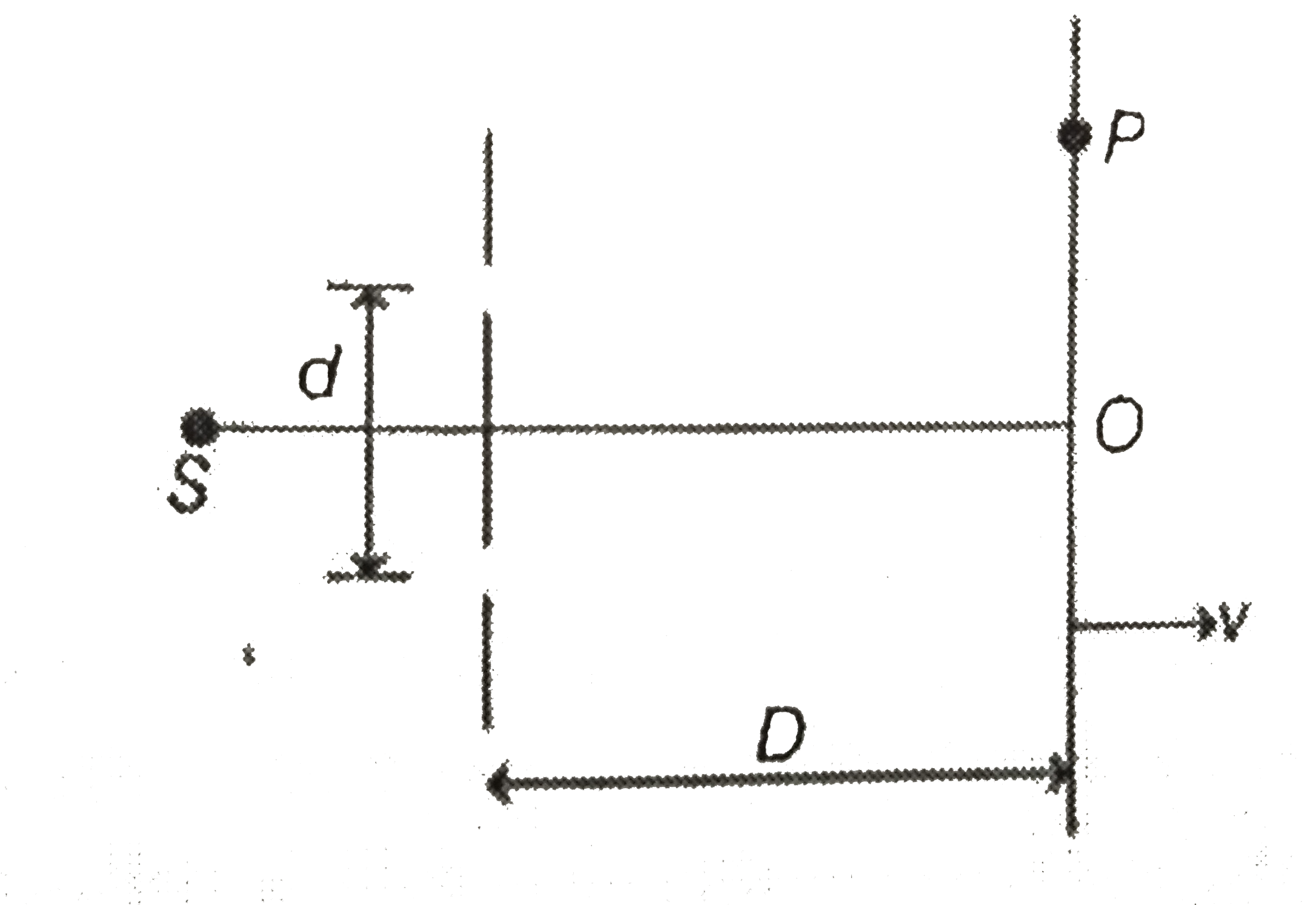
At a point P on the screen the order of fringe will
View Solution
