In Young's double-slit experiment, the slit separation is 0.5 mm and the screen is 0.5 m away from the slit. For a monochromatic light of wavelength 500 nm, the distance of 3rd maxima from the 2nd minima on the other side of central maxima is
2.75 mm
2.5 mm
22.5 mm
2.25 mm
The correct Answer is:d
To solve the problem, we need to find the distance of the 3rd maxima from the 2nd minima on the other side of the central maxima in Young's double-slit experiment. Here are the steps to arrive at the solution:
Step 1: Understand the setup
In Young's double-slit experiment, we have:
- Slit separation (d) = 0.5 mm = 0.5 × 10^(-3) m
- Distance from the slits to the screen (D) = 0.5 m
- Wavelength of light (λ) = 500 nm = 500 × 10^(-9) m
Step 2: Calculate the fringe width (β)
The fringe width (β) is given by the formula:
β=λDd
Substituting the values:
β=(500×10−9 m)(0.5 m)0.5×10−3 m
Step 3: Simplify the calculation
Calculating the above expression:
β=(500×10−9)(0.5)0.5×10−3=250×10−90.5×10−3=250×10−90.5×10−3=0.5×10−3 m=0.5 mm
Step 4: Identify the positions of maxima and minima
- The position of the n-th maxima from the central maximum is given by:
yn=nβ
- The position of the m-th minima is given by:
ym=(m+12)β
Step 5: Calculate the position of the 3rd maxima and the 2nd minima
- For the 3rd maxima (n = 3):
y3=3β=3×0.5 mm=1.5 mm
- For the 2nd minima (m = 2):
y2=(2+12)β=(2.5)β=2.5×0.5 mm=1.25 mm
Step 6: Calculate the distance from the 2nd minima to the 3rd maxima
The distance (Δx) from the 2nd minima to the 3rd maxima is given by:
Δx=y3+y2=1.5 mm+1.25 mm=2.75 mm
Final Answer
The distance of the 3rd maxima from the 2nd minima on the other side of the central maxima is 2.75 mm.
---
In Young's double-slit experiment, we have:
- Slit separation (d) = 0.5 mm = 0.5 × 10^(-3) m
- Distance from the slits to the screen (D) = 0.5 m
- Wavelength of light (λ) = 500 nm = 500 × 10^(-9) m
The fringe width (β) is given by the formula:
β=λDd
Substituting the values:
β=(500×10−9 m)(0.5 m)0.5×10−3 m
Calculating the above expression:
β=(500×10−9)(0.5)0.5×10−3=250×10−90.5×10−3=250×10−90.5×10−3=0.5×10−3 m=0.5 mm
- The position of the n-th maxima from the central maximum is given by:
yn=nβ
- The position of the m-th minima is given by:
ym=(m+12)β
- For the 3rd maxima (n = 3):
y3=3β=3×0.5 mm=1.5 mm
- For the 2nd minima (m = 2):
y2=(2+12)β=(2.5)β=2.5×0.5 mm=1.25 mm
The distance (Δx) from the 2nd minima to the 3rd maxima is given by:
Δx=y3+y2=1.5 mm+1.25 mm=2.75 mm
The distance of the 3rd maxima from the 2nd minima on the other side of the central maxima is 2.75 mm.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct8videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective11videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
In a Young's double slit experiment, the slit separation is 1mm and the screen is 1m from the slit. For a monochromatic light of wavelength 500nm, the distance of 3rd minima from the central maxima is
View SolutionIn a double slit experiment, the two slits are 1mm apart and the screen is placed 1m away. A monochromatic light of wavelength 500nm is used. What will be the width of each slit for obtaining ten maxima of double slit within the central maxima of single-slit pattern?
View Solution
Knowledge Check
- Question 1 - Select One
A narrow slit of width 2 mm is illuminated by monochromatic light fo wavelength 500nm. The distance between the first minima on either side on a screen at a distance of 1 m is
A5 mmB0.5 mmC1 mmD10 mm
In a Young's double slit experiment , the slits are Kept 2mm apart and the screen is positioned 140cm away from the plane of the slits. The slits are illuminatedd with light of wavelength 600nm. Find the distance of the third brite fringe. From the central maximum . in the interface pattern obtained on the screen frings from the central maximum. 3
View SolutionMonochromatic light of wavelength 580 nm is incident on a slit of width 0.30 mm. The screen is 2m from the slit . The width of the central maximum is
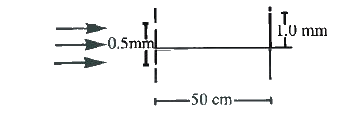
View SolutionWhite coheral light (400 nm 700 nm ) is sent through the slit of a Young.s double slit experiment. The separation between the slits is 0.5 mm and the screen is 50 away from the slits . There is a hole in the screen at a point 1.0 mm away (along the width of the fringes) from the central line. Which wavelengths (s) will be absent in the light coming from the hole ?
 View Solution
View SolutionIn YDSE, the two slits are separated by 0.1 mm and they are
0.5 m from the screen. The wavelength of light used is 5000 Å. Find the distance
between 7th maxima and 11 th minima on the upper side of screen.View SolutionWhite coherent light (400 nm- 700 nm) is sent through the slits of a young.s double slit experiment. The separation between the slits is 0.5mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1 mm from the centre.
In the above problem which wavelength have a strong intensity at the hole?View SolutionIn Young's double slit experiment , the two slits 0.20 mm apart are illuminated by monochromatic light of wavelength 600 nm . The screen 1.0 m away from the slits .
(a) Find the distance of the second (i) bright fringe , (ii) dark fringe from the central maximum .
(b) How will the fringe pattern change if the screen is moved away from the slits ?View SolutionIn a Young's double slit experiment, the separation between the slits = 2.0 mm, the wavelength of the light = 600 nm and the distance of the screen from the slits = 2.0 m. If the intensity at the centre of the central maximum is 0.20Wm−2, what will be the intensity at a point 0.5 cm away from this centre along the width of the fringes ?
View Solution

