Inside a fixed sphere of radius R and uniform density ρ, there is spherical cavity of radius R2 such that surface of the cavity passes through the centre of the sphere as shows in figure. A particle of mass m0 is released from rest at centre B of the cavity. Caculate velocity with which particle strikes the centre A of the sphere. Neglect earth's gravity. Initially sphere and particle are at rest.

The correct Answer is:B, C
Applying conservation of machanical energy,
Increase in kinetic energy
= decrease in gravitational potential energy
or 12m0ν2=UB−UA=mo(VB−VA)
∴ν=√2(VB−VA) ..(i)
Potential at A
VA= potential due to complete sphere
- potential due to cavity
=−1.5GMR−[−GMR/2]
=2GmR−1.5GMR
Hence, m=34π(R2)3ρ=πρR36
and M=43πR3ρ
Substituting the value, we get
VA=GR[πρR33−2πρR3]=−53πGρR2
Potential at B
VB=GMR3[1.5R2−0.5(R2)2]+1.5GmR/2
=−811GMR+3GmR
=GR[πρR32−116.πρR3]=−43πGρR2
∴VB−VA=13πGρR2
So, from Eq. (i)
ν=√23πGρR2
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.1
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
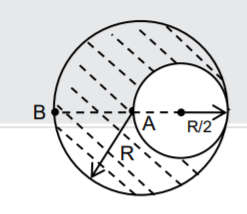
A solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
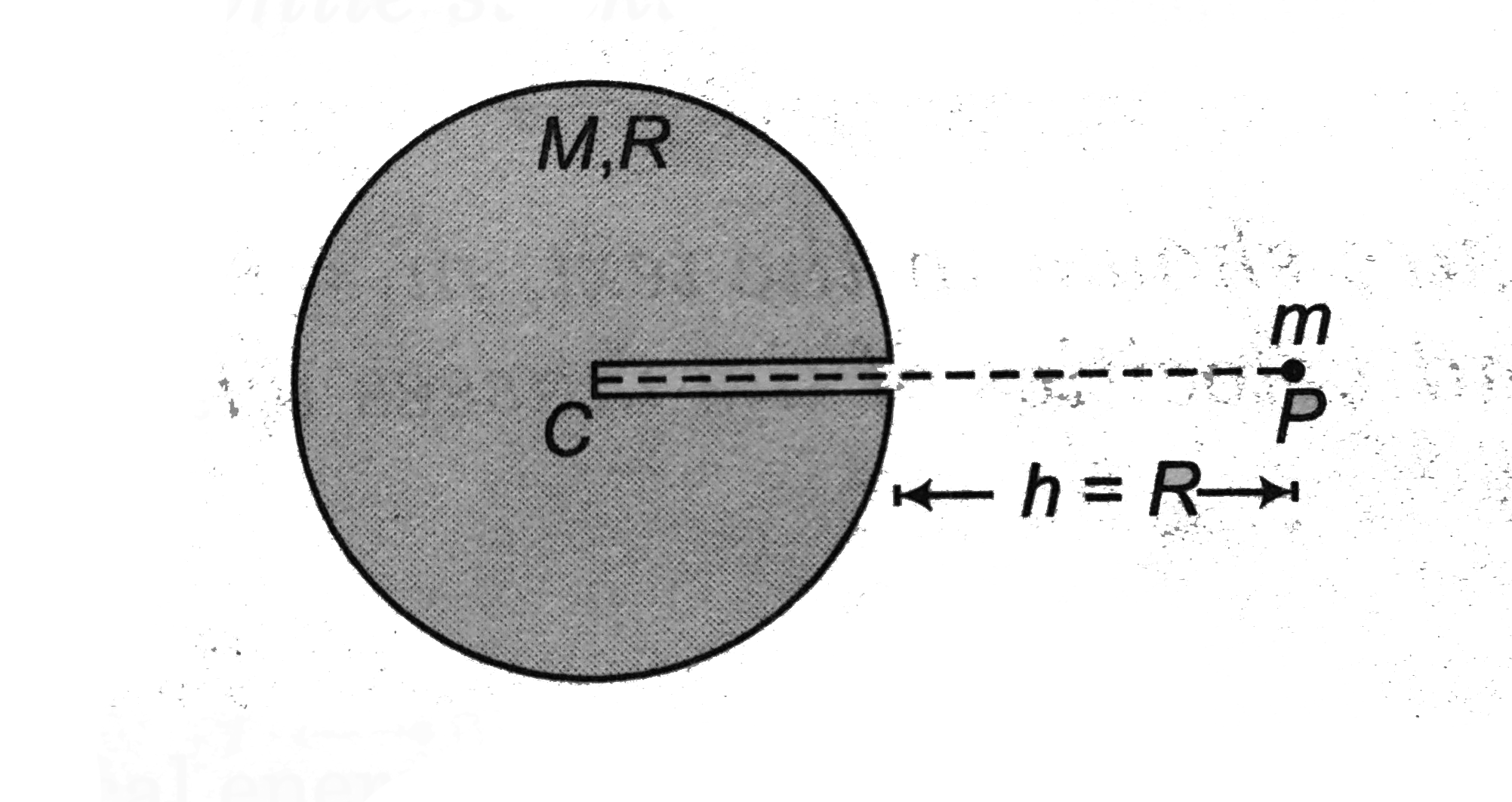
View SolutionThere is a smooth tunnel upto centre C of a solid sphere of mass 'M' and radius R.A particle of mass m(<<M) is released from point P along the line CP. Find velocity of 'm' while striking at C.
 .
.
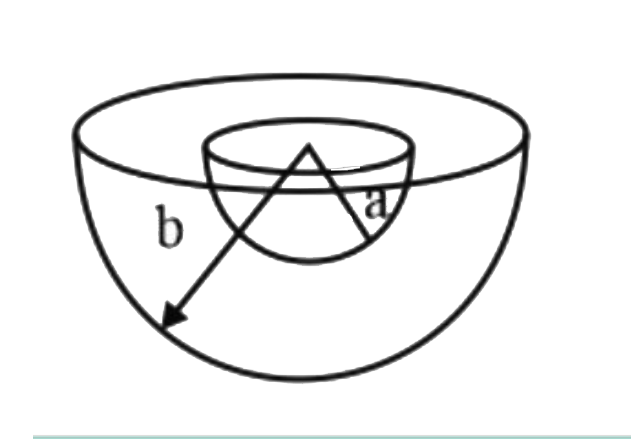
View SolutionA uniform charged hemisphere of radius b and charge density ρ has a hemispherical cavity of radius a(a=b2) cut from its centre . If the potential at the centre of the cavity is nρb216∈0 then n = ?
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?

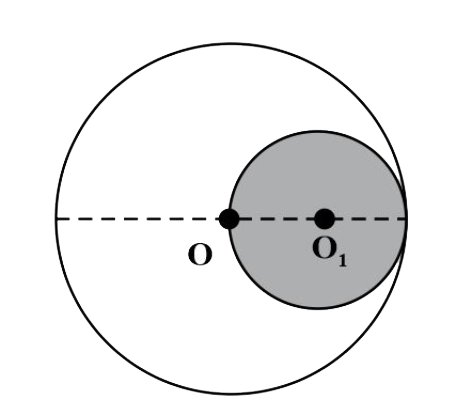
View SolutionA spherical cavity is made in a lead sphere of radius R such that its surface touches the outsides surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this following, is
View SolutionA smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View Solution
