Two planets of equal mass orbit a much massive star (figure). Planet m1 moves in circular orbit of radius 1×108km with period 2yr. Planet m2 moves in an elliptical orbit with closed distance r1=1×108km and farthest distance r2=1.8×108km, as shows.
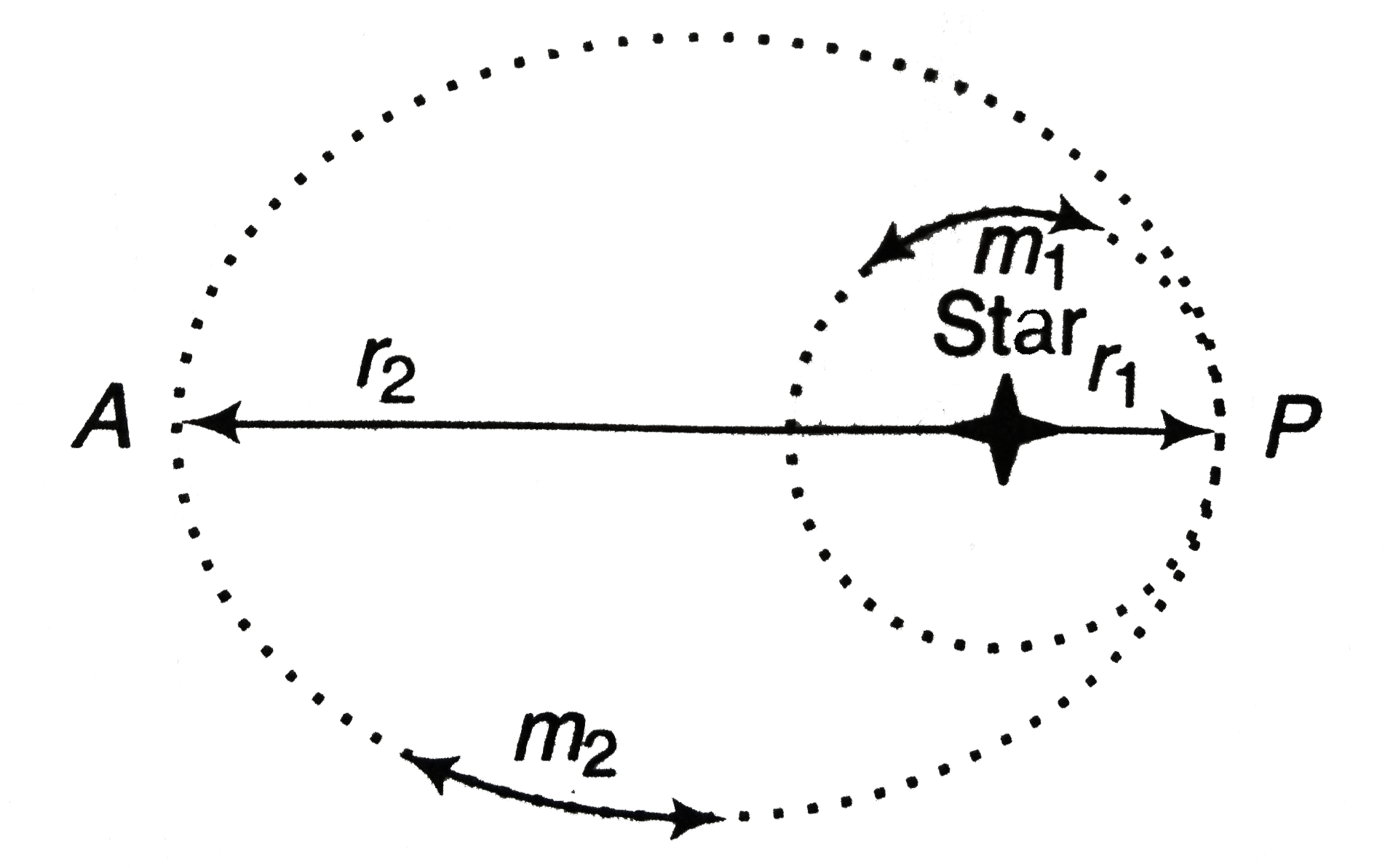
(a) Using the fact that the mean radius of an elliptical orbit is the length of the semi-major axis, find the period of m2's orbit.
(b) Which planet has the greater speed at point P? Which has the greater total energy?
(c ) Compare the speed of planet m2 at P with that at A.
The correct Answer is:A, B, C, D
Mean radius of planet,
m2=r1+r22=1.4×108km
Now, T∝r3/2
∴ Time period of m2 :
T2=T1(1.4×108108)3/2
or T2=2(1.4)3/2
=3.31yr
(b) For m2, point P is perigee position. So, speed at this point is greater than orbit speed for circular orbit.
∴Um2=Um1
∴Em2>Em1
Km2>Km1
(c ) νr= constant
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.120videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.220videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct10videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
In elliptical orbit of a planet
View SolutionThe radius of orbit of a planet is two times that of the earth. The time period of planet is
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
View SolutionA planet is moving round the sun in an elliptical orbit as shows. As the planet moves from A to B
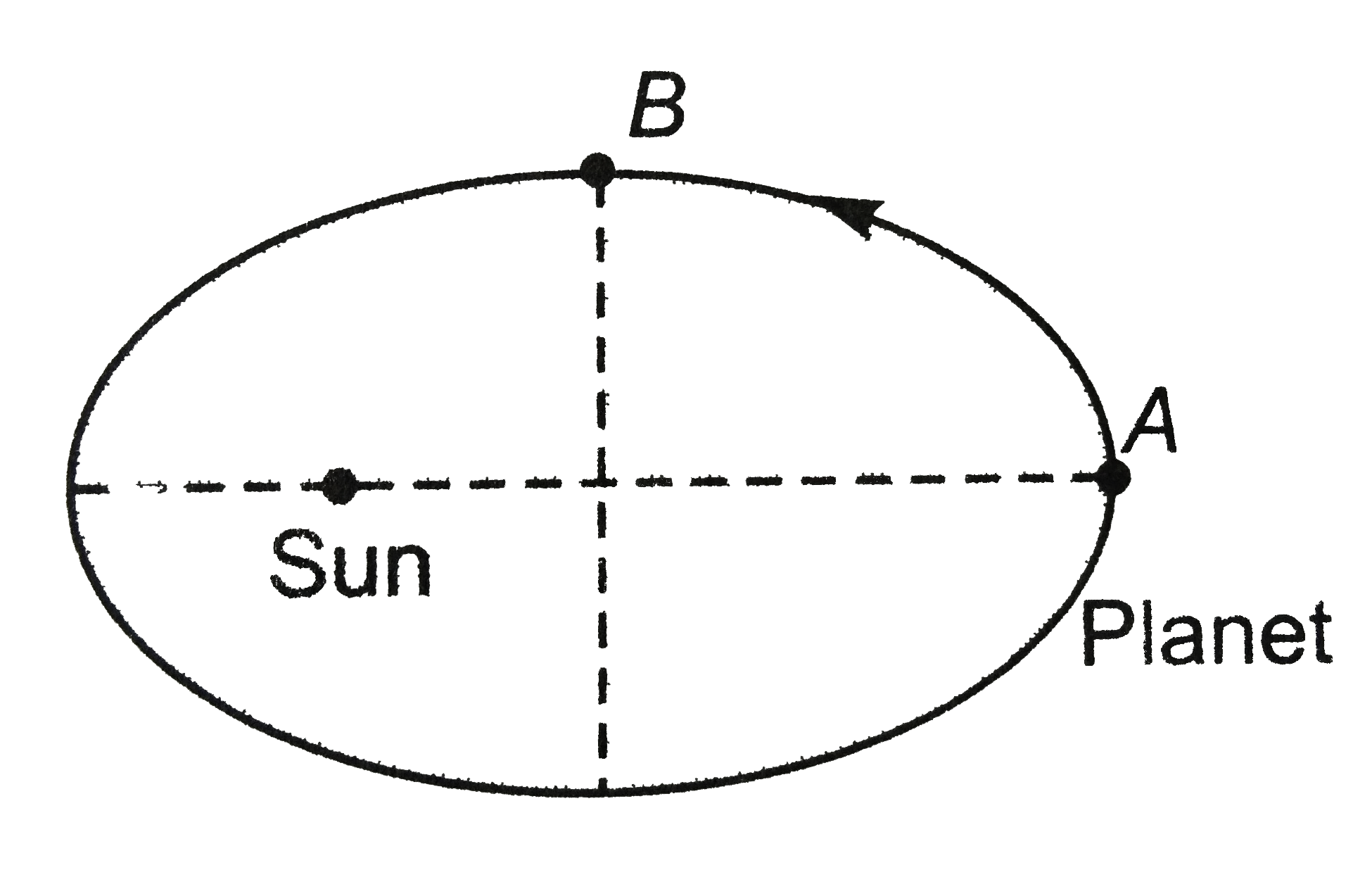 View Solution
View SolutionA plenet moving along an elliptical orbit is closest to the sun at a distance r1 and farthest away at a distance of r2. If v1 and v2 are the linear velocities at these points respectively, then the ratio v1v2 is
View SolutionConsider a planet moving around a star in an elliptical orbit with period T. Area of elliptical orbit is proportional to
View SolutionA planet of mass m is in an elliptical orbit about the sun (m << Msun) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
View SolutionA planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
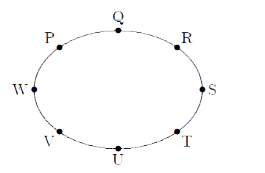 View Solution
View SolutionThe two stars in a certain binary star system move in circular orbits The first star α moves in an orbit of radius 1.00×109km The other star β moves in an orbit of radius 5.00×108km What is the ratio of masses of star β to the star α ? .
View SolutionTwo satellites of masses M and 16 M are orbiting a planet in a circular orbitl of radius R. Their time periods of revolution will be in the ratio of
View Solution

