Inside a smooth hemispherical cavity, a particle P can slide freely. The block having this cavity is moving with constant acceleration a = g (where g is acceleration due to gravity). The particle is released from the state of rest from the topmost position of the surface of the cavity as shown. The angle θ with the vertical, when the particle will have maximum velocity with respect to the block is
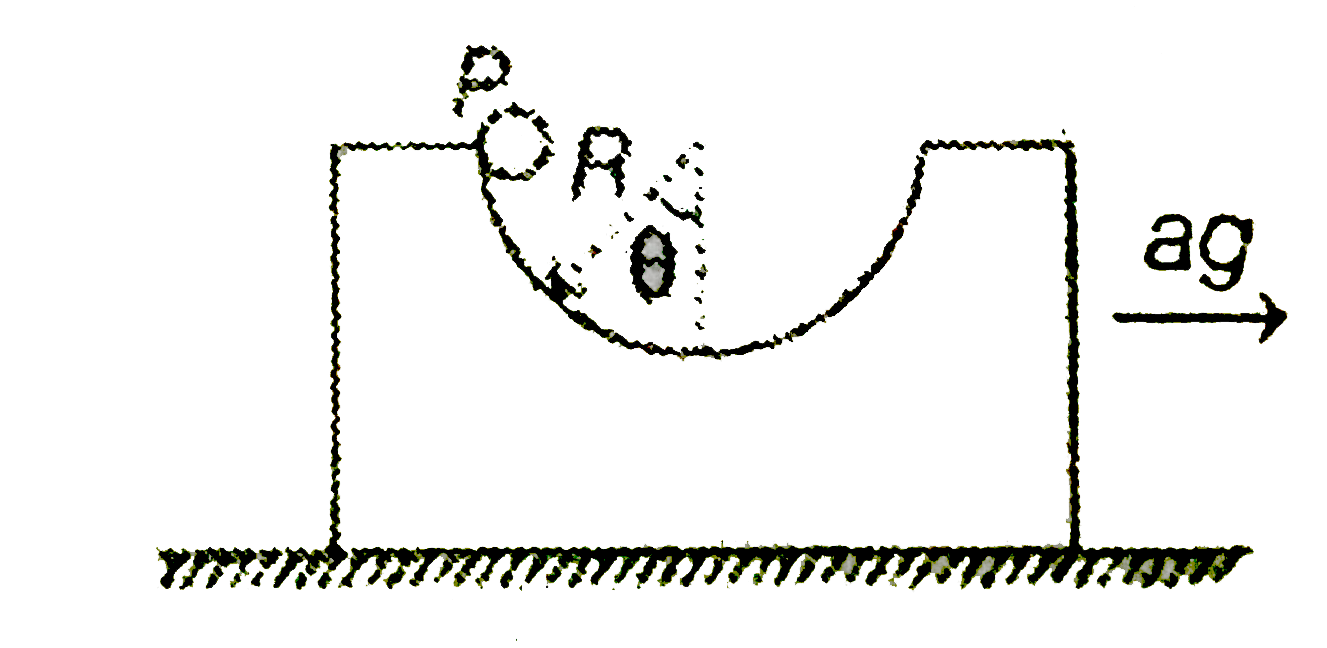
45∘
60∘
30∘
0∘
The correct Answer is:A
Step by step video, text & image solution for Inside a smooth hemispherical cavity, a particle P can slide freely. The block having this cavity is moving with constant acceleration a = g (where g is acceleration due to gravity). The particle is released from the state of rest from the topmost position of the surface of the cavity as shown. The angle theta with the vertical, when the particle will have maximum velocity with respect to the block is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A smooth sphere of radius R is moving in a straight line with an acceleration a. A particle is released from top of the sphere from rest. Find the speed of the particle when it is at an angular position θ from the initial position relative to the sphere.
View SolutionA particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View Solution
Knowledge Check
A particle slides from rest from the topmost point of a vertical circle of radius r along a smooth chord making an angle θ with the vertical. The time of descent is .
ALeast for θ=0BMaximum for θ=0CLeast for θ=45DIndependent of θWhat is the acceleration of block A when the system is released from rest ?
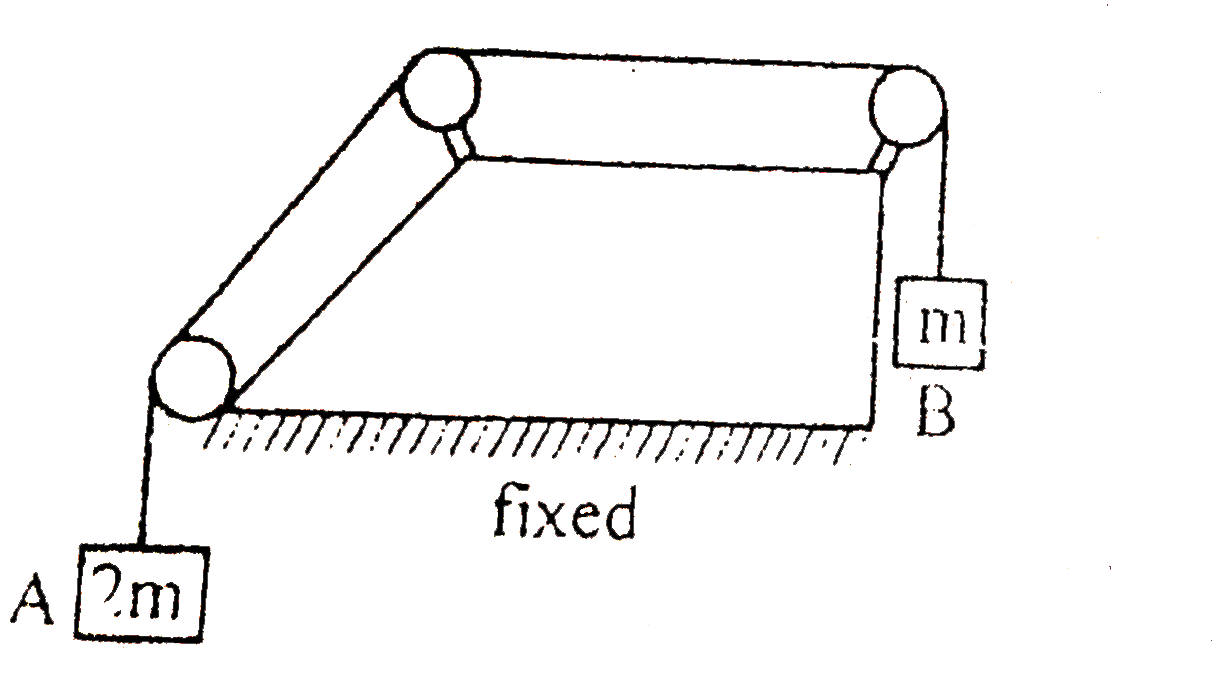 Ag/2 downwardsBg/3 downwardsCg/3 upwardsDg/2 upwards.
Ag/2 downwardsBg/3 downwardsCg/3 upwardsDg/2 upwards.A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
A particle stats from rest at the origin with a constant acceleration
Calculate the position of the particle at t=5 second.
View SolutionIf g is acceleration due to gravity on the surface of the earth,having radius R ,the height at which the acceleration due to gravity reduces to g/2 is
View SolutionThe position, velocity and acceleration of a particle moving with a constant acceleration can be represented by :
View SolutionA particle moves in a plane with constant acceleration in a direction different from the initial velocity. The path of the particle will be
View SolutionIf g is acceleration due to gravity on the surface of the earth, having radius R, the height at which the acceleration due to gravity reduces to g/2 is
View Solution
