Ler l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to
I
Isin2θ
Icos2θ
Icos2(θ2).
The correct Answer is:a
In the figure, A′B′ is perpendicular to AB
C′D′ is perpendicular to CD
By symmetry, IAB=IA′B′
ICD=IC′D′
By theorem of perpendicular axes,
IZ=IAB+IA′B′=2IAB .............(i)
Again, IZ=ICD+IC′D′=2ICD ..............(ii)
∴ From (i) and (ii),
2IAB=2ICD or IAB=ICD or I=ICD
Hence moment of inertia about CD axis= I.

Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - NCER EXAMPLAR PROBLEMS
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ASSERTION AND REASON
15 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ROLLING MOTION
16 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions
150 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals.
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals.
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is
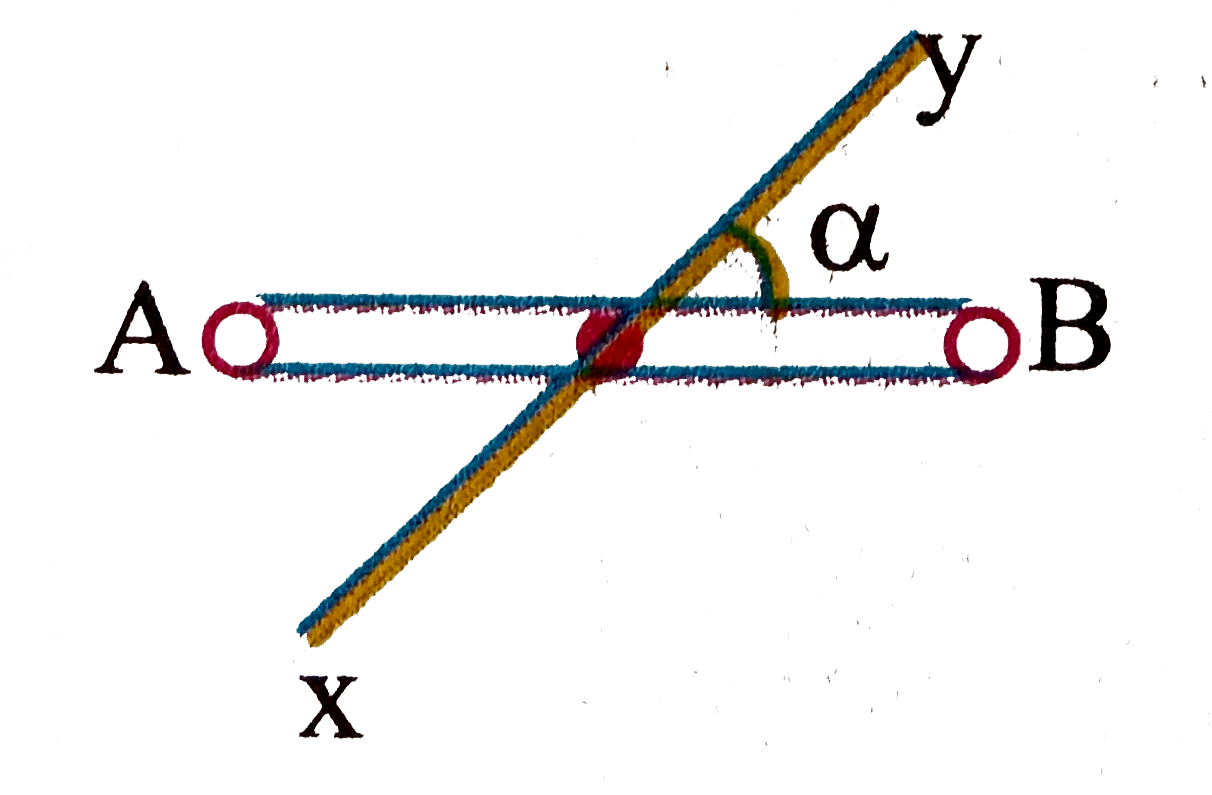
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to plate is
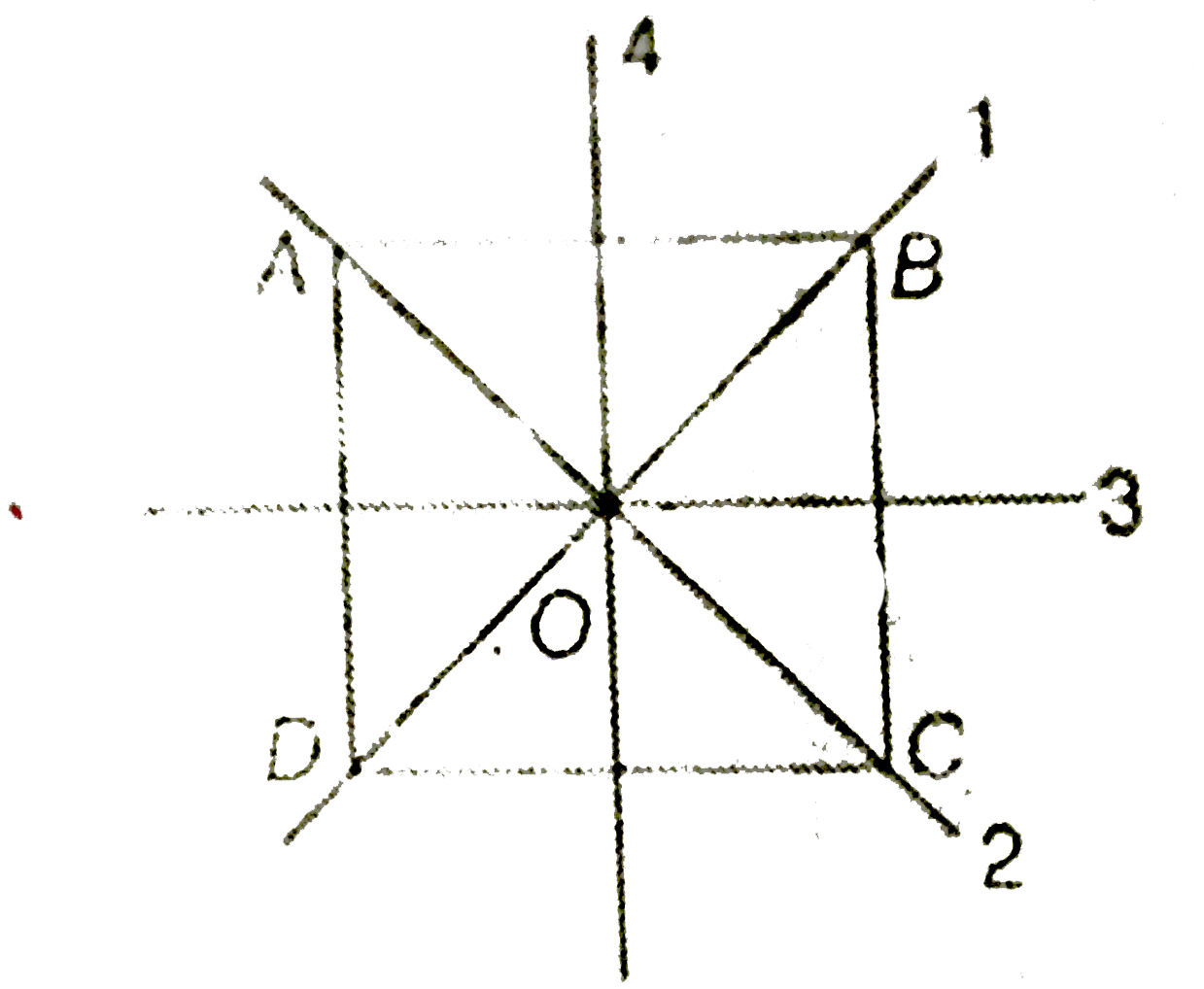
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View Solution
