Mass of solid floating in liquid is m1 and mass of liquid is m2. Base area is A. Then pressure at bottom is p0+(m1+m2)gA
Reason : Upward force on liquid from base of vessel is pA, where p is pressure at bottom.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:B
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Match the columns
Explore 6 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Medical entranes gallery
Explore 49 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Taking it together
Explore 157 Videos
- EXPERIMENTSBook:DC PANDEYChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
The following equation gives a relation between the mass m1 kept on a surface of area A and the pressure p exerted on this area.
p(m1+m2x)A
What must be the dimensions of the quatities x and m2?
View SolutionThe following equation gives a relation between the mass m1 kept on a surface of area A and the pressure p exerted on this area.
p=(m1+m2)xA
What must be the dimensions of the quatities x and m2?
View Solution
Knowledge Check
An object weights m1 in a liquid of density d1 and that in liquid of density d2 is m2. The density of the object is
Am2d2−m1d1m2−m1Bm1d1−m2d2m2−m1Cm2d1−m1d2m1−m2Dm1d2−m2d1m1−m2The mass of block is m1 and that of liquid with the vessel is m2 The block is suspended by a string (tension T) partically in the liquid. The reading of the weighing machine placed below the vessel
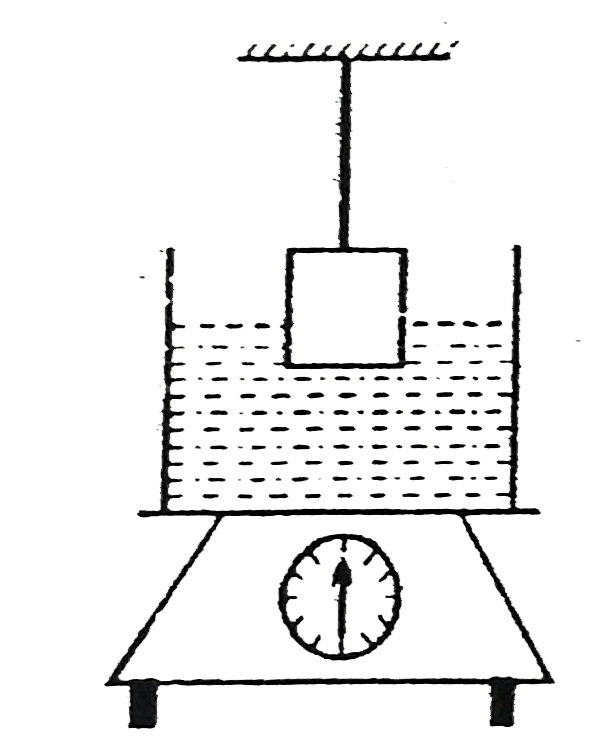 Acan be (m1+m2)gBcan be greater than (m1+m2)gCis equal to (m1g+m2−T)Dcan be less than (m1+m2)g
Acan be (m1+m2)gBcan be greater than (m1+m2)gCis equal to (m1g+m2−T)Dcan be less than (m1+m2)g
The following equation gives a relation between the mass m1 kept on a surface of area A and the pressure p exerted on this area.
p=(m1+m2)xA
What must be the dimensions of the quatities x and m2?
View SolutionIf equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View SolutionThe small orifice between two communicating vessels have area 1 sq. cm. The surface area of horizontal sections of the first and the second vessel are 10m2 and 5m2. Initially the level of liquid in the first and second vessel is 15 m and 5 m from the orifice. Given that velocity of liquid flow is v=σ√2g(h1−h2) m/s, where h1 and h2 is the height of liquid in the two vessels, then the time required for the liquid to reach the same level is 10t15σ√20g, where t is equal to _?
View SolutionAlong the line - 1, mass of gas m1 and pressure is p1. Along the line - 2 mass of same gas is m2 and pressure is p2. Choose the correct options.
 .
.
View SolutionTwo identical cyclindrical vessels (area of cross section 3.5×10−3m2) with their bases at the same level contain liquid of density 800kg/m3. The height of liquid in one vessel is 0.3 m and in the other it is 0.1m. Assuming g=10m/s2, find the workdone by gravity in equalising levels when the vessels are interconnected at bottom.
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )
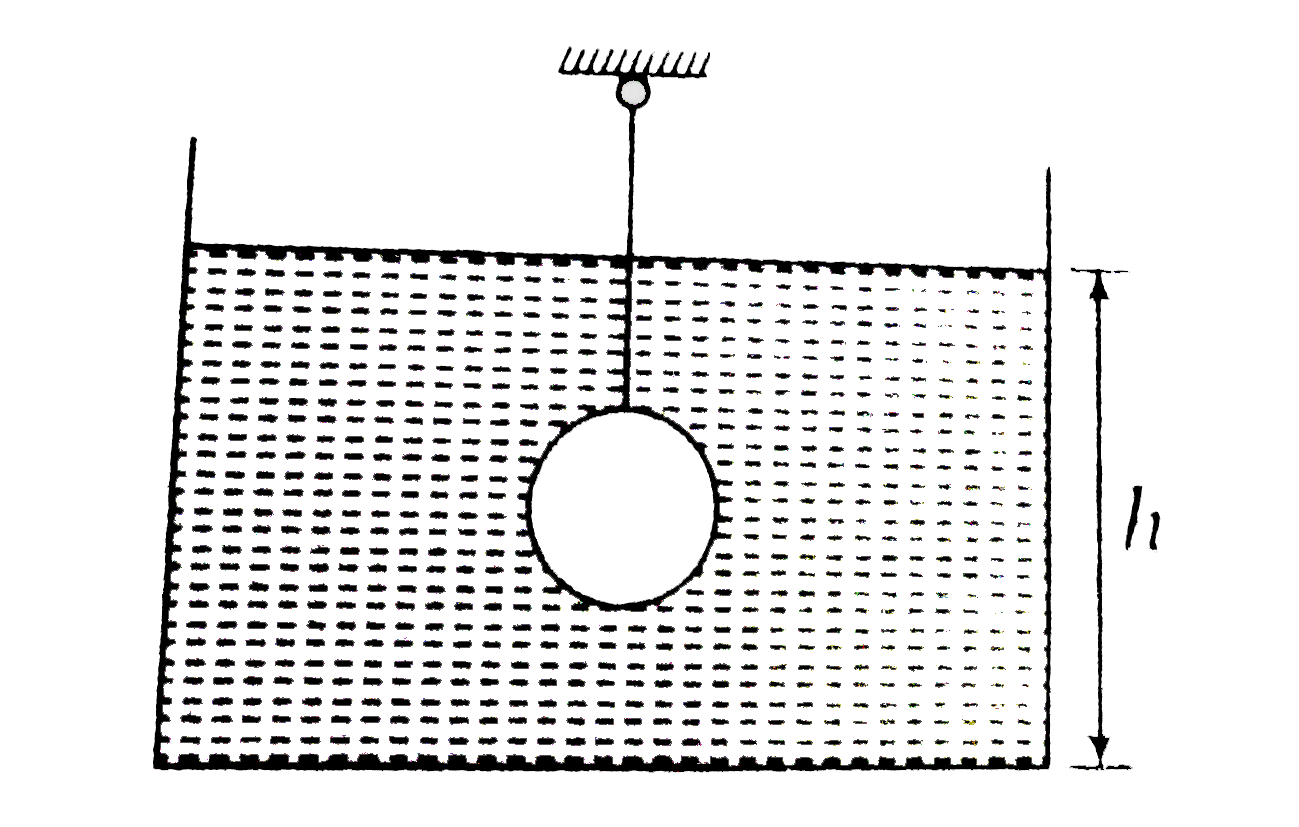
View Solution
